ORB! Alpha 达到年化 36%
这个策略来自 Carlo Zarattini 等人,在 Quantpedia 2023 年大赛中获第三名。他们研究了最近 6 年的美股市场,发现聚焦在热门股 (Stocks in Play) 中时,5 分钟 ORB 策略实现了超过 1600%的总净收益,夏普高达 2.81,年化 Alpha 为 36%。同期标普只有 198%。
这个策略简单暴力,只利用了量比、ATR 和 5 分钟突破等非常简单的技巧。数年以前,有个朋友通过机器学习,得到过一个两周翻倍的策略,我一直没好意思问他实现细节。但通过他的调仓记录来看,最终实现的效果与此庶几近之。
ORB 策略最早由 Toby Crabel 于 1990 年提出,他在《Day trading with short term price patterns and opening range breakout》一书中,详细地介绍了这个策略及系统实现。此后,无论是产业界还是学界都在持续探索和改进这个策略。
2023 年,Carlo Zarattini 等人在 ORB 的基础上,加入了 stocks in play 的限制,将策略的夏普提升到 2.81,年化 Alpha 则达到惊人的 36%(扣除交易费用,参考巴菲特的 20%左右,大奖章的 39%左右)。
选股过滤器
Zarattini 等人提出的策略有以下过滤器:
- 开盘价要超过$5。
- 过去 14 天平均成交量超过 1 百万股
- 14 天 ATR 要超过$0.5
- 量比至少为 2,并且
- 只交易量比为前 20 的个股
交易执行
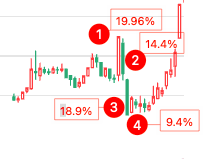
根据开盘前 5 分钟的方向,确定当日交易方向。比如,如果开盘头 5 分钟为阳线,则考虑在该股上做多;反之做空。如果头 5 分钟为阳线,即使后面是向下突破,也不考虑做空。
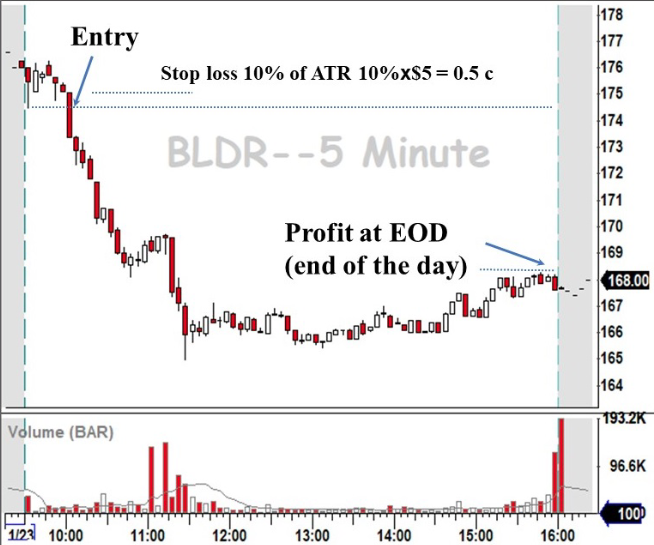
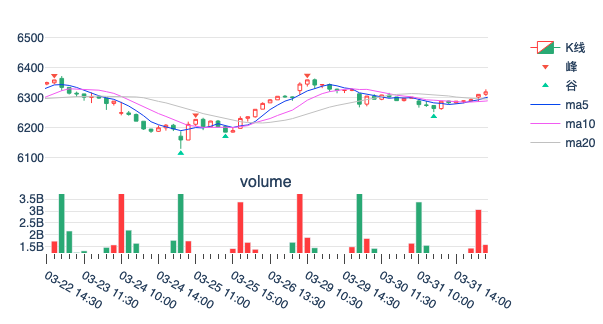
在上图中(注意红色为阴线、空心为阳线),个股以阴线开盘,因此当天的交易方向确定为做空。10 点,股价向下突破(超过头 5 分钟最低价),开空仓,并在 10% ATR 处下止损单。当日尾盘卖出。
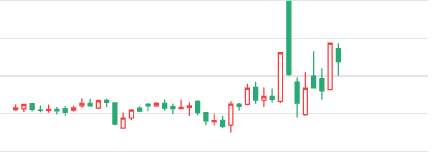
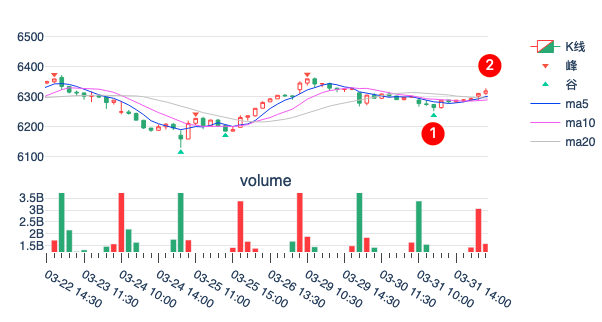
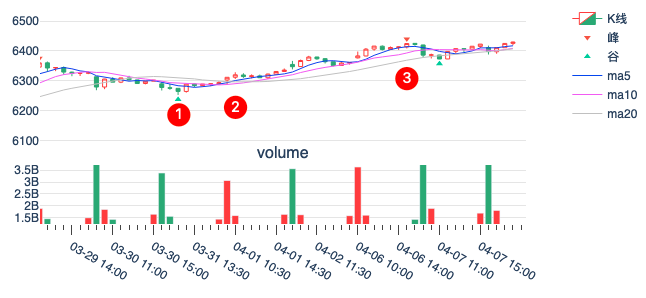
下图则是另外两个例子,分别显示了在做多和做空情况下,何时开仓。左图的例子特别提示了,并不是每一次开仓都能获利,仍然有风险因素要考虑。
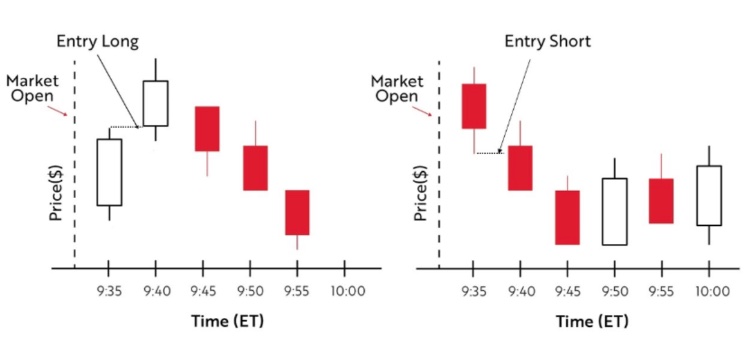
关于这个策略,如果你还在期待我讲更多,很遗憾。我讲完了。
大道至简。
请原谅我用了一句割韭菜的老师们常用的一句话。不过,毕竟咱们是做量化的,高低也得整几句理论的。接下来,就是见证数学公式和金融理论的时刻。
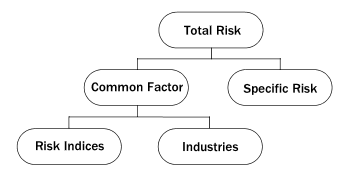
Why it works?
Zarattin 策略成功的关键不是 ORB 策略本身,而是通过条件过滤器,筛选出来了一个独特的小宇宙 (universe)。这个小宇宙的居民,都是高能粒子,有足够的波动性。
另外,由于有美股 T+0 和做空的特性,可以实现斩断亏损,让利润奔跑(通过 ATR 及仓位控制,让每支股票即使亏损,对组合的冲击也控制在 1%以内)。
Tip
A 股没有 T0 和个股做空手段(不是所有的券都能融到),但并不意味着这个策略不能在 A 股应用。
我们逐一解释一下过滤器中的条件。
股价大于$5,不用多解释,可怜之人,亦必有可恨之处。低价股便宜总有便宜的理由。
过去 14 天平均成交量超过 1 百万股。这一条尽管有多种解释,但它在短线操作中的作用,就是要保证成交活跃,这样交易时才不会有太大的冲击成本。
14 天 ATR 超过 0.5,是要保证股性活跃。ATR 是一个绝对值,我们也可以用 20 天均线值转换成百分比,这样可以得到一个适合所有标的的 ATR 标准。
第 4 和第 5 条是选股器的战斗机! 量比是关键,是信号发射器,只此一手,选出热门股 (stock in play)。第 4 条主要是保证在整体市场清淡的情况下,还能保证选出的个股满足要求。
如果你是一些割韭菜号的读者,你很可能听他们这样讲早盘选股策略:
Quote
集合竞价时,把量比前 10 的个股加入自选,观察到 10:50,上涨且涨幅不超过 3%,下探时不破分时均线的,买!
如果这些策略没有一定的合理性,是不可能割到韭菜的。
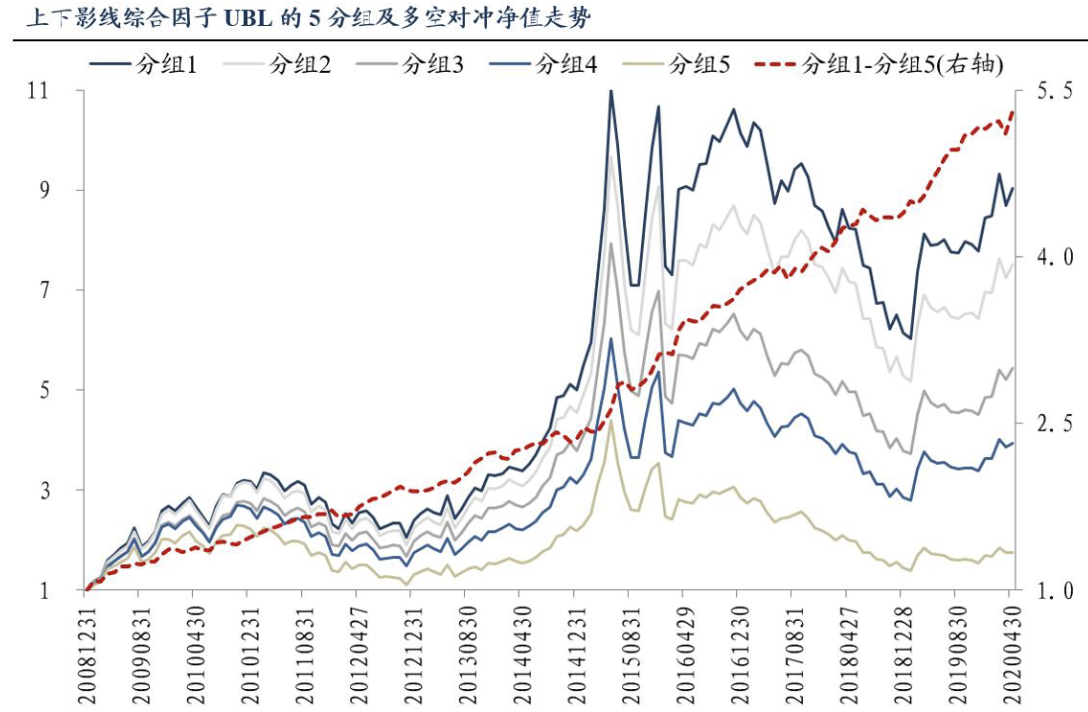
Zarattin 等基于大量的数据统计,发现了量比与盈利能力(含多空双边)之间的统计相关性,证明了选股老司机的理论有合理性。见下图:
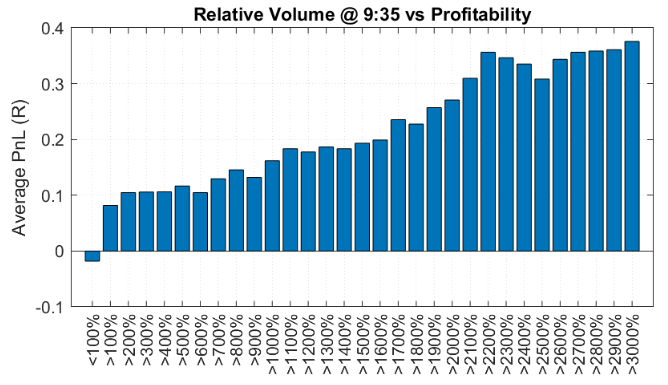
这里的量比就是大家理解的量比,为严谨起见,我们也把他们的计算公式也发布出来:
这里\(ORVolume_{t,j}\)是个股 \(j\) 在 \(t\) 日前 5 分钟的成交量,\(ORVolume_{t-i,j}\)则是个股\(j\)在\(t-i\)日前 5 分钟的成交量。
从数据上看,只选择量比超过 30 倍的个股,看起来性价比更高。但根据 Zarattin,这样实际上会减少一年之中的交易机会,进而减少了总盈利。
除了基于统计数据之外,我更关心策略背后的经济和博弈原理。量比放大究竟意味着什么?如果搞清楚这一点,我们就能知道这一关键因子会不会失效,如果会,何时失效。
用好一个因子,比挖掘新的因子更重要。因为大道至简,趋动股票上涨的因素,说破天,也无非就是那么几种。
在有经验的短线交易者之间,一直流传着只做热门股的策略。一家公司可能因为这些信息的披露而成为热门股:
- 超预期的收益报告披露或者预披露。
- 专利、药品、许可的批准或者撤销。
- 重组和收购或者建立战略联盟、伙伴关系。
- 重要产品发布、拿下重要合同(或者在竞标中失去)或者客户。
- 管理层变动
- 股票拆分(本文作者:即送转)、回购、发债
- 突破关键技术点位。
除第 7 点之外,其背后都蕴含着公司盈利能力变动的信息。因此,一旦这些信息被公布,往往就会引来众人的关注,提醒他们去交易该股。无论这些信息是在盘中发布的、还是盘后发布的,人们在晚上都有充分的时间来接收、消化这些信息,并且为第二天早间的操作做出决策。
因此,如果某家公司在头一天有 breaking news 放出来,第二天的成交量就一定会比前一天大许多;反过来,如果一支股票的成交量突然放大,则往往也意味着该公司出现了超预期的消息。
如何预测这些消息对方向决定作用呢?分析师往往是屁股指挥脑袋,别听他们的。也别自己分析,因为股票这个事,你分析正确没用,只要其他人都分析错了,你分析正确也白搭。
ORB 策略告诉我们,看早盘 5 分钟的方向。如果是阳线,大概率是做多,如果是阴线,大概率是做空。
股市是赤裸裸的金钱民主。大家用钱来决定方向,非常真诚。
为什么要强调量比?因为如果做多时成交量没有明显放大,意味着交易的人仍然是场内资金,场内资金往往会做骗线。只有大量的场外资金涌入时,金钱博弈出来的方向才是真实的方向。
如果有人想改变这个方向,他就得拿出更多的钱来。他想高调,但实力他也不允许啊。这样确定的方向,像极了渣男的爱情,它可能短暂,但每一次都很真诚。
现在,你还要用大模型来进行文本挖掘,进行预测吗?还是开始相信,一切信号,都蕴藏在量价之中?
百闻不如一练。在大富翁量化环境中,我们提供了2005年以来的分钟级数据,回测支持到分钟,你可以亲自己试一下这个策略。
Tip
写给随机游走和 EMH 学说爱好者。这两个学说在股票市场上没有一席之地(但在期货和期权上是正确的)。
熬夜的人看不到早间新闻。市场主体接收、消化以及响应这些信息的时间绝不可能同步。
公司经营所得的利润总在源源不断地注入股市,股市总的来说正方向的(当然不包括缅甸)。
它前进的步伐在大时间跨度上,会大于 GDP 的增长速度,因为股市里聚集的应该是一国最好的公司。
在 A 股的应用
要做到文章所说的收益率和低风险,需要满足两个条件,一是要能 T0 止损。第二个则与市场无关:你需要有一套量化交易系统,能快速计算出全市场 5 分钟量比,能够快速下单,一键止损。原文虽然提到了做空,但仅做多也是 OK 的。
但在 A 股,我们无法做到 T0 止损,这会放大一些风险。如果可能,可以考虑转债品种。
原文(PDF)还研究了不同时间窗口(10, 15, 30 等)下的 ORB 策略,并且提供了加量比约束与不加量比约束的策略对比。需要原文的读者请转发本文后索取。















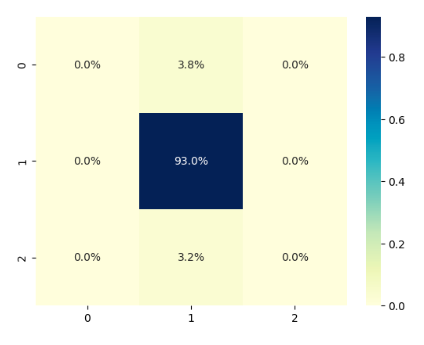
 在这次实验中,我们将使用XgBoost。
在这次实验中,我们将使用XgBoost。