为什么Q-Q图可用来进行统计推断

Table of Content

原理¶

假设有一个随机变量，我们想知道它是否服从某种分布，我们是否能够通过可视化的方式对它进行判定？

解决这个问题，需要用到 Q-Q 图，即 Quantile-Quantile 图，又称分位图，它是可视化统计推断的重要手段。

首先，我们有这样一个事实：

如果 X 是一个数据集，那么$[X, X]$在二维平面上的图像将是完全落在一条 45 度角的直线上的散点图；
如果有另外一个数据集 Y，将 X 与 Y 分别排序后，如果任意坐标位$i$上的$X_i$和$Y_i$完全相等，我们仍将得到相同的图形；
如果任意坐标位$i$上的$X_i$和$Y_i$都近似相等，我们将得到分布在这条直线两侧不远处的散点图。

X = stats.norm.rvs(size=1000)
Y = stats.norm.rvs(size=1000)

plt.scatter(sorted(X), sorted(Y), s=1)
plt.plot(X, X, color='orange')

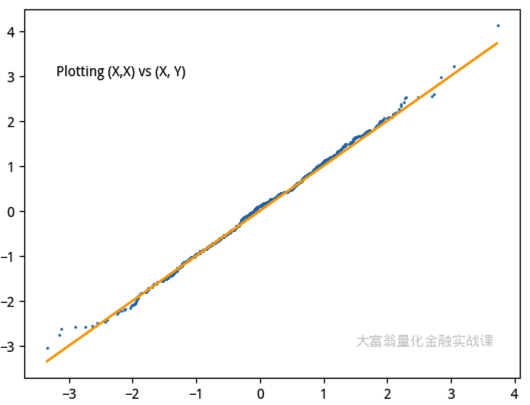
上面的例子中，我们从标准正态分布中抽样分别抽样两次，得到$X$和$Y$，对它们进行排序后进行绘图，就得到了一个分布在 45 度直线两侧的散点图。

实际上，上面的例子已经给了我们一个判别某个分布是否属于标准正态分布的一个算法。这里我们需要解释一下，为什么对属于同一分布的$X$和$Y$，进行排序后，对应位置的元素应该大致相等。这就需要引入分位数的概念。

如果我们有随机变量 X，假设它服从标准正态分布，那么在 50%分位处，X 的采样点$x_1$应该非常接近于 0（由于是随机变量，所以也很难完全相等），因为标准正态分布，在 50%分位处的取值就是 0；推广到 25%分位处，75%分位处，$X$在这些分位数上的取值，也应该与标准正态分布取值非常接近；或者进一步推广，在任意分位数处，两者的采样值都应该非常接近。

因此，按照分位数分别对$X$和标准正态分布进行采样，再进行绘图，这样的图形就是一个分布在 45 度直线两侧的散点图。

在实际绘图中，我们会简化上述算法，不去进行分位数计算，而是以排序进替代。将 X 与 Y 排序后，如果样本总数是 N，那么排序后的第$n$个元素，就被认为是第 $n/N$分位数处的随机变量取值；如果第$n$个元素处的$X_n$与$Y_n$非常接近，那么点$[X_n, Y_n]$将落在直线 $Y = X$ 附近，也就是 45 度角的直线上。

这种简化，在 n 值较大时，是完全生效的；在 n 值较小时，有可能出现较大偏差。

下面的代码演示了当 n 从 10 开始，依次倍增到 1280 时的绘图：

fig, axes = plt.subplots(nrows=2, ncols=4, figsize=(16,8))
axes = axes.flatten()

for i, n in enumerate((10, 20, 40, 80, 160, 320, 640, 1280)):
    X = stats.norm.rvs(size=n)
    Y = stats.norm.rvs(size=n)

    ax = axes[i]
    ax.scatter(sorted(stats.zscore(X)), sorted(Y), s=3)
    ax.plot(X, X, '--', color='grey')

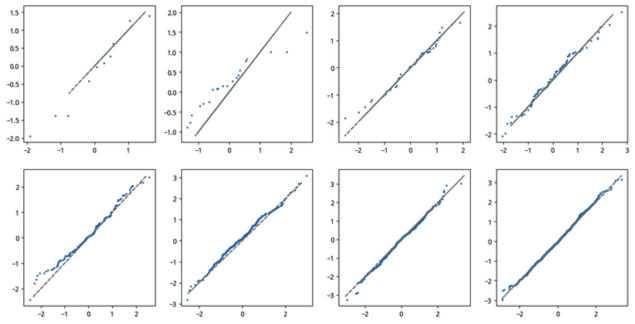
从图中可以看出，当 n 大于等于 320 时，大多数点都落在直线两侧附近。

任意正态分布检验¶

如果$X$是一个 norm(loc, scale) 的正态分布，那么，如果我们仍以 [$X, $Y] 绘图，我们会得到一个分布在直线$Y = (X - loc)/scale $两侧的散点图。

np.random.seed(78)
loc = 5
scale = 3
X = stats.norm.rvs(loc=loc, scale = scale, size=1000)
Y = stats.norm.rvs(size=1000)

plt.scatter(sorted(X), sorted(Y), s=1)
plt.plot(X, X, color='orange')

x2 = np.linspace(min(X), max(X), len(X))
y2 = x2 / scale - loc / scale
plt.plot(x2, y2, color='cyan')

plt.text(5, 5, "[X,X]")
plt.text(10, 2, "[X,Y]", color='blue')
plt.text(10, 3.5, "[X, (X-loc)/scale]", color='red')

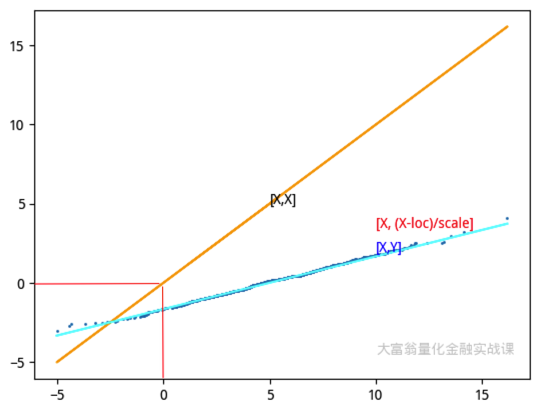
我们也可以考虑先将$X$进行 zscore 化，这样再与标准正态分布的采样进行绘图。如果$X$服从正态分布，此时得到的图形，仍然是多数点分布在$y=x$直线两侧的散点图。

能绘制 Q-Q 图的库¶

上面的代码已经给出了绘制方法，但主要是帮助我们了解其原理。实际运用中，我们可以借助 scipy.stats 中的 probplot 方法：

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

# GENERATE A RANDOM DATASET FOLLOWING A NORMAL DISTRIBUTION
np.random.seed(0)
data = np.random.normal(loc=5, scale=2, size=100)

# GENERATE A Q-Q PLOT
plt.figure(figsize=(8, 8))
stats.probplot(data, dist="norm", plot=plt)
plt.title('Q-Q plot')
plt.ylabel('Sample quantiles （样本分位数）')
plt.xlabel('Theoretical quantiles （理论分位数）')
plt.grid(True)
plt.show()

当然现在我们明白，probplot 方法只不过是按照我们提供的 dist 参数，在内部生成了同样长度的理论分布采样数据，对待检验分布和理论分布都进行排序，然后绘制回归直线与散点图而已。

上述代码将绘制出这个图形：

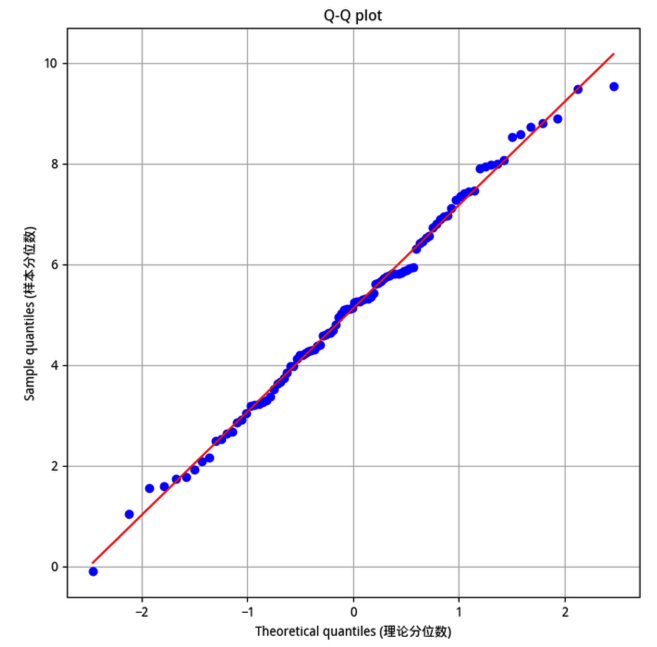
另外，在 statsmodels 库中，也通过 graphics.gofplots 提供了 qqplot 方法。