量化策略中如何进行缩放和归一化

---

Table of Content

缩放和归一化是机器学习中必然遇到的一个问题。在量化策略中，不管是否用到机器学习，我们也常常遇到类似问题。

在《大富翁量化金融实战课》第12课中，对这个问题进行了较深入的讨论。这篇文章既是对该课内容的一个摘要，也是加入了一些新的思考，可以独立成篇。

从数学上看，缩放（归一化）是从一个值域映射到另一个值域的过程。这种映射，有的是线性的（比如min-max scale），有时候则需要非线性映射，比如，我们常常需要将一个\((-\infin, +\infin)\)的区间映射到\((-1, 1)\)或者\((0, 1)\)上。

从量化交易的角度看，WR指标（William's R)就是一个典型的min-max scale，它的公式如下：

\[ WR = \frac{max(high) - close}{max(high) - min(low)} \]

Attention

在量化交易中使用min-max scale一定要非常小心。
它主要存在两个问题。
其一是它引入了未来数据（但不是在所有情况下都会引入未来数据，比如William's R在实时计算时，是不存在未来数据的；但在回测中是否引入未来数据，就要看你怎么用了。
其二是，使用经过min-max scale处理的数据来进行预测，预测值一定在[min, max]区间内。但是，股价不存在确定的min/max。如果我们根据当下经过min-max scale处理后的数据来预测未来的股价，预测出来的股价是不可能突破当下见到的最大值的，而实际上，股价是可以涨上天的。
与之对比，在鸢尾花数据集中，我们对花瓣的长度和宽度都可以进行min-max scale，因为我们的采样基本上能够代表总体，未来也基本上不会出现明显超出采样中的min/max的。

更多的时候，在量化中我们需要进行非线性映射。比如，我们曾经介绍过，地量是一种比较重要的交易信号。地量见地价。什么是地量？我们可以用当前成交量是多少个周期以来的最低值来度量。这个数值最小为1，最大可以是10天，也可以是一个月，一年或者更长，因此，它的取值范围从数学上看是\([1, +\infin]\)。

在第13课，我们介绍圆弧底的评价函数时，也讲到过圆弧底的宽度区间可能在\([3, +\infin)\)之间。

对这种值域范围不确定的，我们一般可以用S型函数来进行变换。这些函数包括：

\[ f(x) = sigmoid(x) = \frac{1}{1 + e^{-x}} \tag 1 \]

\[ f(x) = tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \tag 2 \]

\[ f(x) = \frac{x}{1+|x|} \tag 3 \]

\[ f(x) = \frac{x}{sqrt(1 + x^2)} \tag 4 \]

特殊情况下，如果我们的采样数据存在周期性特点，而且我们希望在变换后，保留它们在周期上的关联性，也可以用\(sin\)和\(cos\)函数。这种归一化方法，在著名的《attention is all you need》一文中就使用过（对token的位置进行编码）：

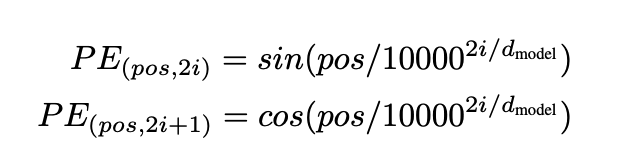
考虑到股价波动的周期性，也许类似的方法也应该在量化中找到运用。

但是，使用sigmoid函数来进行归一化也存在一些问题。比如在地量那个例子中，13个周期以来的地量，与120天以来的地量相比，显然两者具有完全不同的信号含义：一支个股很容易出现13个周期以内的地量，而很难出现120个周期以内的地量。一旦出现，很容易出现一定幅度的反弹。

然而，如果我们对其进行sigmoid归一化的话，它们的取值将会是一样的：

def sigmoid(x):
    return 1/(1 + np.exp(-x))

print("sigmoid(12) == sigmoid(13)?", np.isclose(sigmoid(12), sigmoid(13)))

从上例可以看出，实际上，当\(x > 12\)时，在计算中我们就已经无法区分函数值之间的差异了。

因此，在使用中，我们一般要对sigmoid进行一些修改，使之在某个区间内，具有较高的响应灵敏度。公式如下：

\[ f(x) = \frac{2}{1+e^{-\frac{ln(40000)}{b}.(x-b)+ln(0.005)}} - 1 \]

此时图形主要由参数b决定。当b为15时，图形如下：

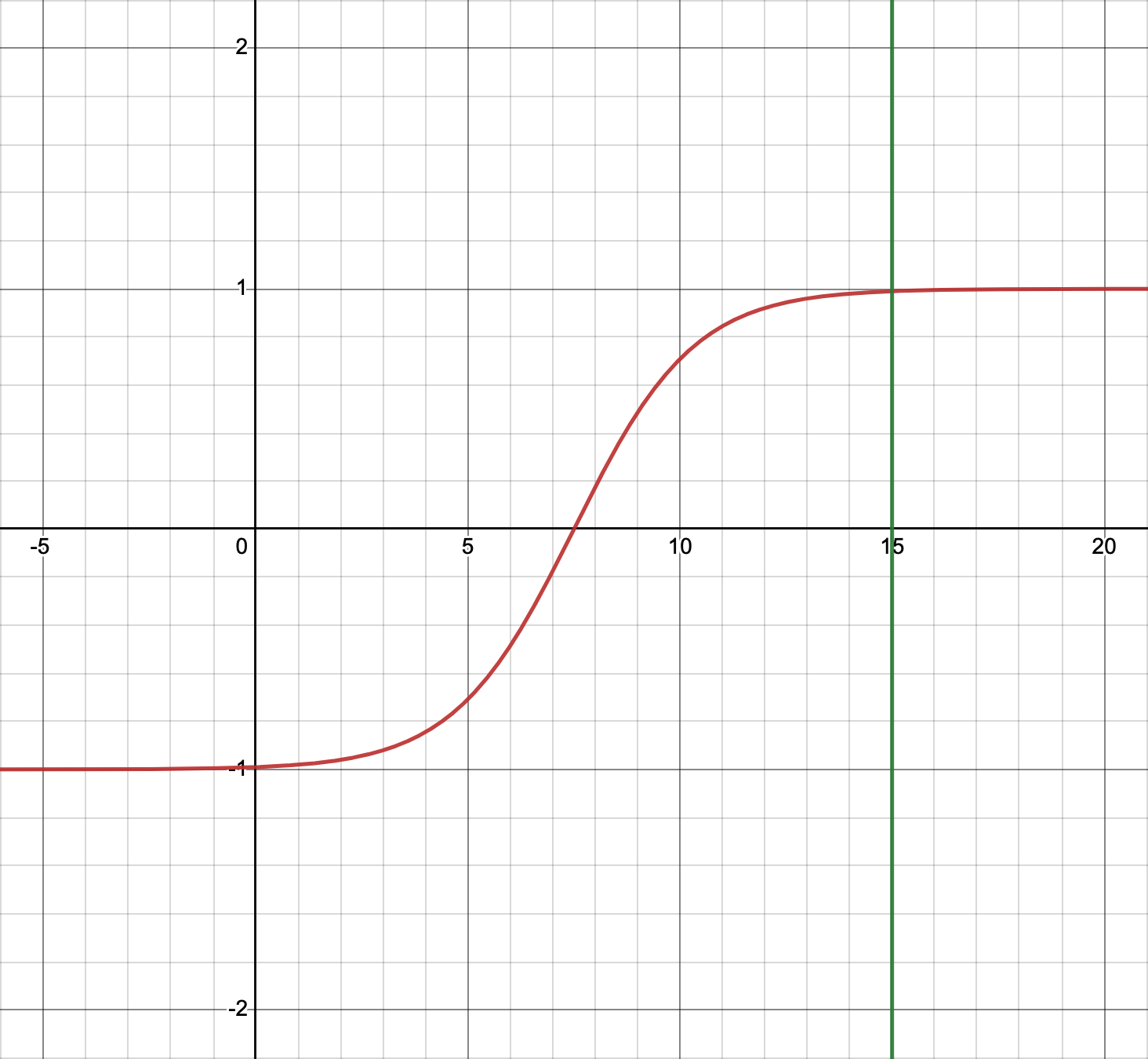
该分布区间为[-1, 1]，x取值在[0,b]之间时分布密度较高。

在非机器学习型的量化打分策略中，我们可能倾向于函数值域落在[0,1]之间（想想看，RSI和WR都在这个区间内，而不是[-1,1]）。所以，我们对上述公式略加修改，代码实现如下：

import matplotlib.pyplot as plt

def scaled_sigmoid(x, start, end):
    """当`x`落在`[start,end]`区间时，函数值为[0,1]且在该区间有较好的响应灵敏度
    """
    n = np.abs(start - end)

    score = 2/(1 + np.exp(-np.log(40_000)*(x - start - n)/n + np.log(5e-3)))
    return score/2


fig, (ax1, ax2, ax3,ax4) = plt.subplots(nrows = 1, ncols = 4, figsize=(12,3))

x = np.linspace(0, 1)
ax1.plot(x, [scaled_sigmoid(i, x[0], x[-1]) for i in x])
ax1.set_title("fit (0,1)")

x = np.linspace(0, 100)
ax2.plot(x, [scaled_sigmoid(i, x[0], x[-1]) for i in x])
ax2.set_title("fit (0, 100)")

x = np.linspace(18, 38)
ax3.plot(x, [scaled_sigmoid(i, x[0], x[-1]) for i in x])
ax3.set_title("fit (18, 38)")

x = np.linspace(0, 100)
ax4.plot(x, [sigmoid(i) for i in x])
ax4.set_title("fit (0,100) with original")

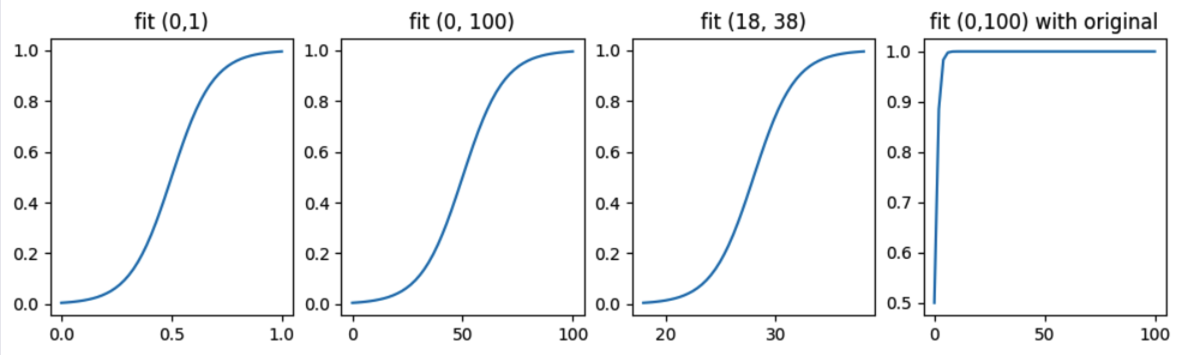
从上图可以看出，与原来的sigmoid相比，新的scaled_sigmoid函数在[start, end]区间有很好的响应灵敏度，此区域内的分布密度最高。