algo »

快速傅里叶变换与股价预测研究

Table of Content

一个不证自明的事实：经济活动是有周期的。但是，这个事实似乎长久以来被量化界所忽略。无论是在资产定价理论，还是在趋势交易理论中我们几乎都找不到周期研究的位置 -- 在后者语境中，大家宁可使用“摆动”这样的术语，也不愿说破“周期”这个概念。

这篇文章里，我们就来探索股市中的周期。我们将运用快速傅里叶变换把时序信号分解成频域信号，通过信号的能量来识别主力资金，并且根据它们的操作周期进行一些预测。最后，我们给出三个猜想，其中一个已经得到了证明。

FFT - 时频互转¶

（取数据部分略）。

我们已经取得了过去一年来的沪指。显然，它是一个时间序列信号。傅里叶变换正好可以将时间序列信号转换为频域信号。换句话说，傅里叶变换能将沪指分解成若干个正弦波的组合。

# 应用傅里叶变换
fft_result = np.fft.fft(close)
freqs = np.fft.fftfreq(len(close))

# 逆傅里叶变换
filtered = fft_result.copy()
filtered[20:] = 0
inverse_fft = np.fft.ifft(filtered)

# 绘制原始信号和分解后的信号
plt.figure(figsize=(14, 7))
plt.plot(close, label='Original Close')
plt.plot(np.real(inverse_fft), label='Reconstructed from Sine Waves')
plt.legend()

我们得到的输出如下：

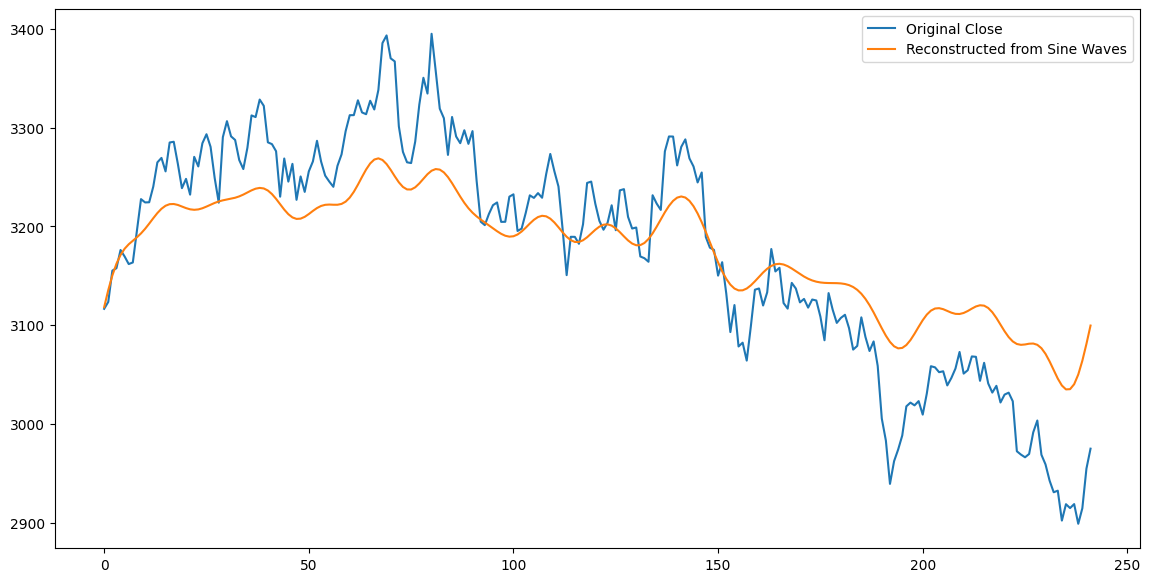
在数字信号处理的领域，时间序列被称为时域信号，经过傅里叶变换后，我们得到的是频域信号。时域信号与频域信号可以相互转换。Numpy 中的 fft 库提供了 fft 和 ifft 这两个函数帮我们实现这两种转换。

np.fft.fft 将时域信号变换为频域信号，转换的结果是一个复数数组，代表信号分解出的各个频率的振幅 -- 也就是能量。频率由低到高排列，其中第 0 号元素的频率为 0，是直流分量，它是信号的均值的某个线性函数。

np.ff.ifft 则是 fft 的逆变换，将频域信号变换为时域信号。

将时域信号变换到频域，就能揭示出信号的周期性等基本特征。我们也可以对 fft 变换出来的频域信号进行一些操作之后，再变换回去，这就是数字信号处理。

高频滤波和压缩¶

如果我们把高频信号的能量置为零，再将信号逆变换回去，我们就会得到一个与原始序列相似的新序列，但它更平滑 -- 这就是我们常常所说的低通滤波的含义 -- 你熟悉的各种移动平均也都是低通滤波器。

在上面的代码中，我们只保留了前 20 个低频信号的能量，就得到了与原始序列相似的一个新序列。如果把这种方法运用在图像领域，这就实现了有损压缩 -- 压缩比是 250/20。

在上世纪 90 年代，最领先的图像压缩算法都是基于这样的原理 -- 保留图像的中低频部分，把高频部分当成噪声去掉，这样既保留了图像的主要特征，又大大减少了要保存的数据量。

当时做此类压缩算法的人都认识这位漂亮的小姐姐 -- Lena，这张照片是图像算法的标准测试样本。在漫长的进化中，出于生存的压力，人类在识别他人表情方面进化出超强的能力。所以相对于其它样本，一旦压缩造成图像质量下降，肉眼更容易检测到人脸和表情上发生的变化，于是人脸图像就成了最好的测试样本。

Lena 小姐姐是花花公子杂志的模特，这张照片是她为花花公子 1972 年 11 月那一期拍摄的诱人照片的一小部分 -- 在原始的照片中，Lena 大胆展现了她诱人的臀部曲线，但那些不正经的科学家们只与我们分享了她的微笑 -- 从科研的角度来讲，这也是信息比率最高的部分。无独有偶，在 Lena 成为数字图像处理的标准测试样本之前，科学家们一直使用的是另一位小姐姐的照片，也出自花花公子。

好，言归正传。我们刚刚分享了一种方法，去掉信号中的高频噪声，使得信号本身的意义更加突显出来。我们也希望在证券分析中使用类似的技法，使得隐藏在 K 线中的信号显露出来。

但如果我们照搬其它领域这一方法，这几乎就不算研究，也很难获得好的结果。实际上，在证券信号中，与频率相比，我们更应该关注信号的能量，毕竟，我们要与最有力量的人站在一边。

所以，我们换一个思路，把分解后的频域信号中，能量最强的部分保留下来，看看它们长什么样。

过滤低能量信号¶

# 保留能量最强的前 5 个信号
amp_threshold = np.sort(np.abs(fft_result))[-11]

# 绘制各个正弦波分量
plt.figure(figsize=(14, 7))

theforce = []
for freq in freqs:
    if freq == 0:  # 处理直流分量
        continue
    elif freq < 0:
        continue
    else:
        amp = np.abs(fft_result[np.where(freqs == freq)])
        if amp < amp_threshold:
            continue
        sine_wave = amp * np.sin(2 * np.pi * freq * np.arange(len(close)))
        theforce.append(sine_wave)
        plt.plot(dates, sine_wave, label=f'Frequency={freq:.2f}')

plt.legend()
plt.title('Individual Sine Wave Components')
ticks = np.arange(0, len(dates), 20)
labels_to_show = [dates[i] for i in ticks]
plt.xticks(ticks=ticks, labels=labels_to_show, rotation=45)
plt.show()

FFT 给出的频率总是一正一负，我们可以简单地认为，负的频率对我们没有意义，那是一种我们看不到、也无须关心的暗能量。所以，在代码中，我们就忽略了这一部分。

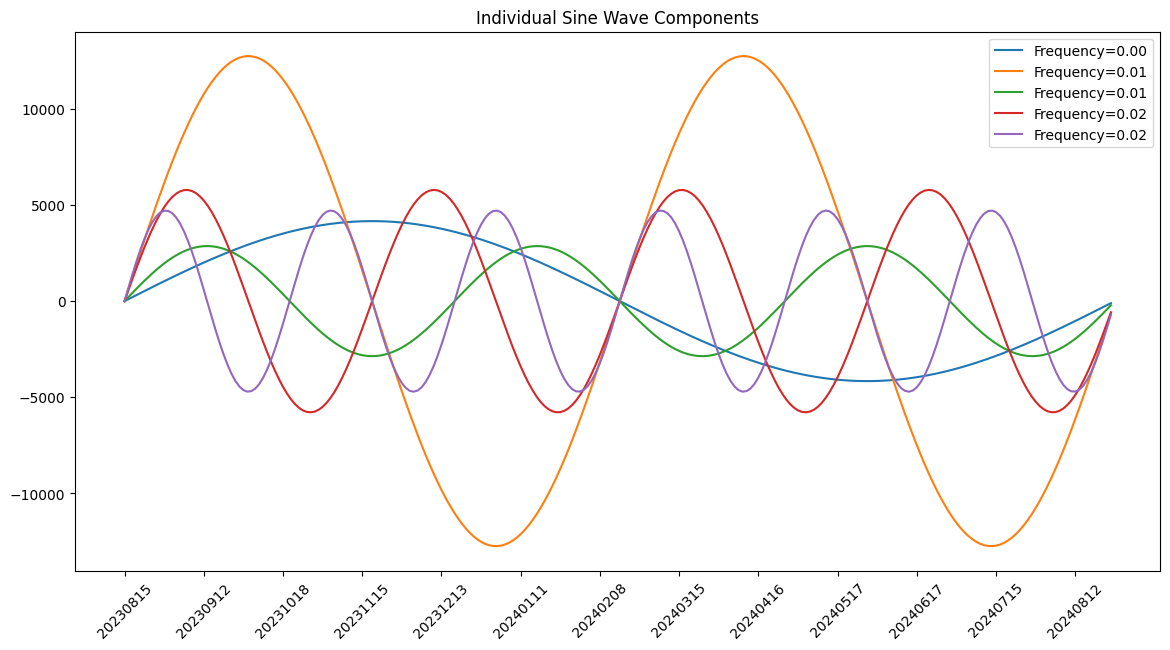
我们看到，对沪指走势影响最强的波（橙色）的周期是 7 个月左右：从峰到底要走 3 个半月，从底到峰也要走 3 个半月。由于它的能量几乎是其它波的一倍，所以它是主导整个叠加波的走势的：如果其它波与它同相，叠加的结果就会使得趋势加强；反之，则是趋势抵消。其它几个波的能量相仿，但频率不同。

这些波倒底是什么呢？它可以是一种经济周期，但是说到底，经济周期是人推动的，或者反应了人的判断。因此，我们可以把波动的周期，看成资金的操作周期。

从这个分解图中，我们可以猜想，有一个长线资金（对应蓝色波段），它一年多调仓一次。有一个中线资金（对应橙色波段），它半年左右调一次仓。其它的资金则是短线资金，三个月左右就会做一次仓位变更。还有无数被我们过滤掉的高频波段，它们操作频繁，可能对应着散户，但是能量很小，一般都可以忽略；只有在极个别的时候，才能形成同方向的叠加，进而影响到走势。

现在，我们把这几路资金的操作合成起来，并与真实的走势进行对比，看看情况如何：

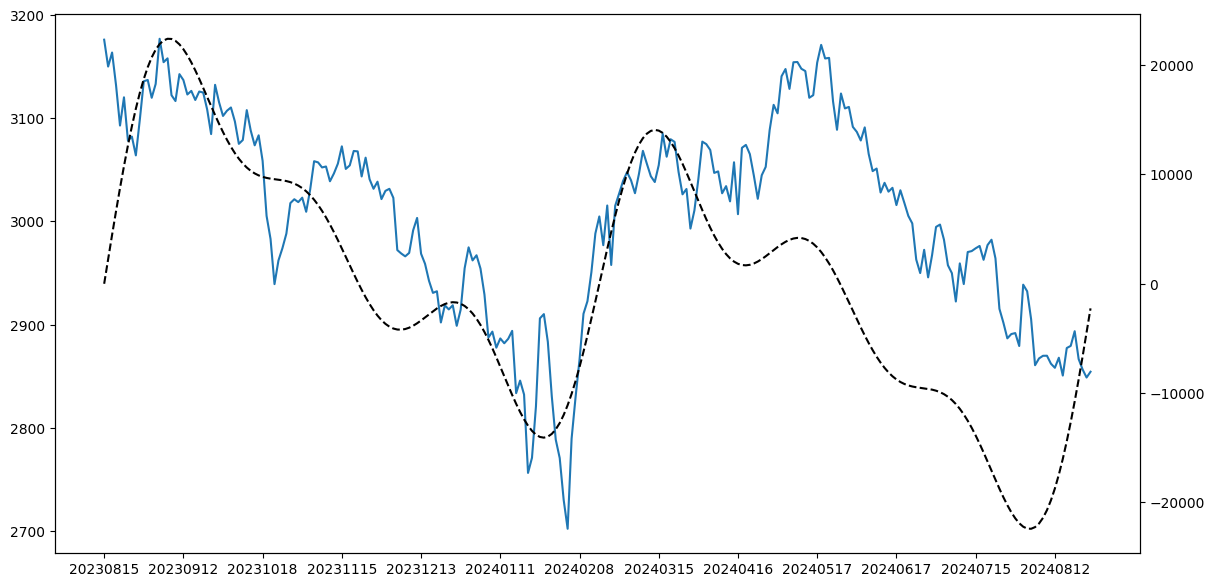
在大的周期上都基本吻合，也就是这些资金基本上左右了市场的走势。而且，我们还似乎可以断言，在 3 月 15 到 5 月 17 这段时间，出现了股价与主力资金的背离趋势：主力资金在撤退了，但散户还在操作，于是，尽管股价还在上涨，但最终的方向，由主力资金来决定。

Tip

黑色线是通过主力资金波段合成出来的（对未来有预测性），在市场没有发生根本性变化之前，主力的操作风格是相对固定的，因此，它可能有一定的短时预测能力。如果我们认可这个结论的话。那么就应该注意到，末端部分还存在另一个背离 -- 散户还在离场，但主力已经进场。当然，关于这一点，请千万不要太当真。

关于直流分量的解释¶

我过去一直以为直流分量表明资产价格的趋势，但实际上所有的波都是水平走向的 -- 但只有商品市场才是水平走向的，股票市场本质上是向上的。所以，直流分量无法表明资产价格的趋势。

直到今天我突然涌现一个想法：如果你把一个较长的时序信号分段进行 FFT 分解，这样会得到若干个直流分量。这些直流分量的回归线才是资产价格的趋势。

这里给出三个猜想：

如果分段分解后，各个频率上的能量分布没有显著变化，说明投资者的构成及操作风格也没有显著变化，我们可以用 FFT 来预测未来短期走势，直到条件不再满足为止。
沪指 30 年来直流分量应该可以比较完美地拟合成趋势线，它的斜率就等于沪指 20 年回归线的斜率。
证券价格是直流分量趋势线与一系列正弦波的组合。

下面我们来证明第二个猜想（过程略）。最终，我们将直流分量及趋势线绘制成下图：

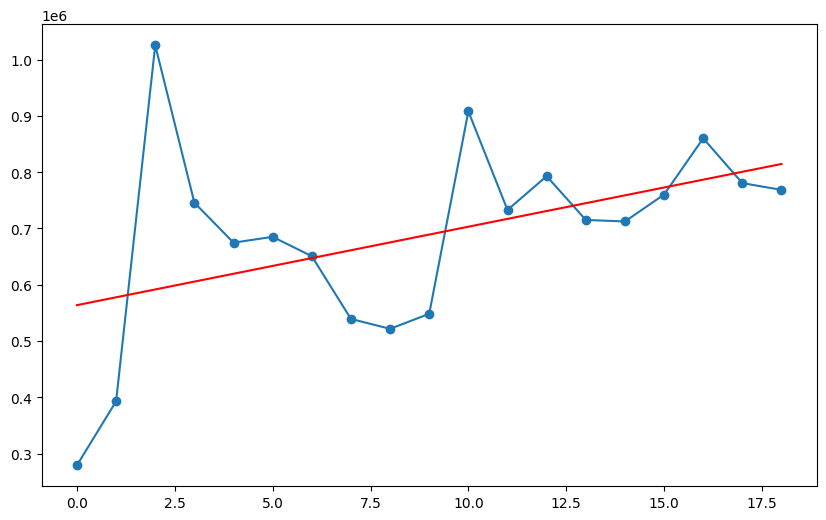
而 2005 年以来的 A 股年线及趋势线是这样的：

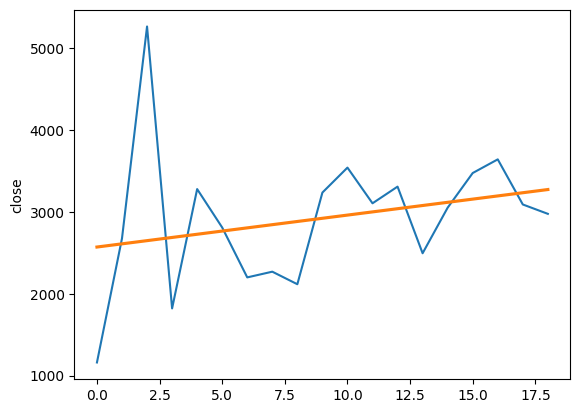
不能说十分相似，只能说几乎完全一致。

趋势线拟合的 p 值是 0.055 左右，也基本满足 0.05 的置信度要求。

本文复现代码已上传到我们的课程环境，加入我们的付费投研圈子即可获得。

这篇文章是我们《因子分析与机器学习策略》中的内容，出现在如何探索新的因子方法论那一部分。对 FFT 变换得到的一些重要结果，将成为机器学习策略中用以训练的特征。更多内容，我们课堂上见！