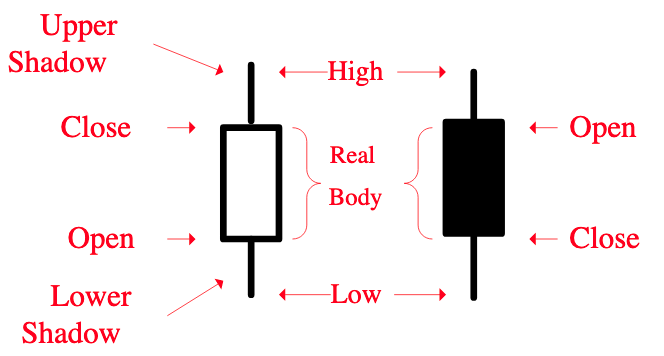
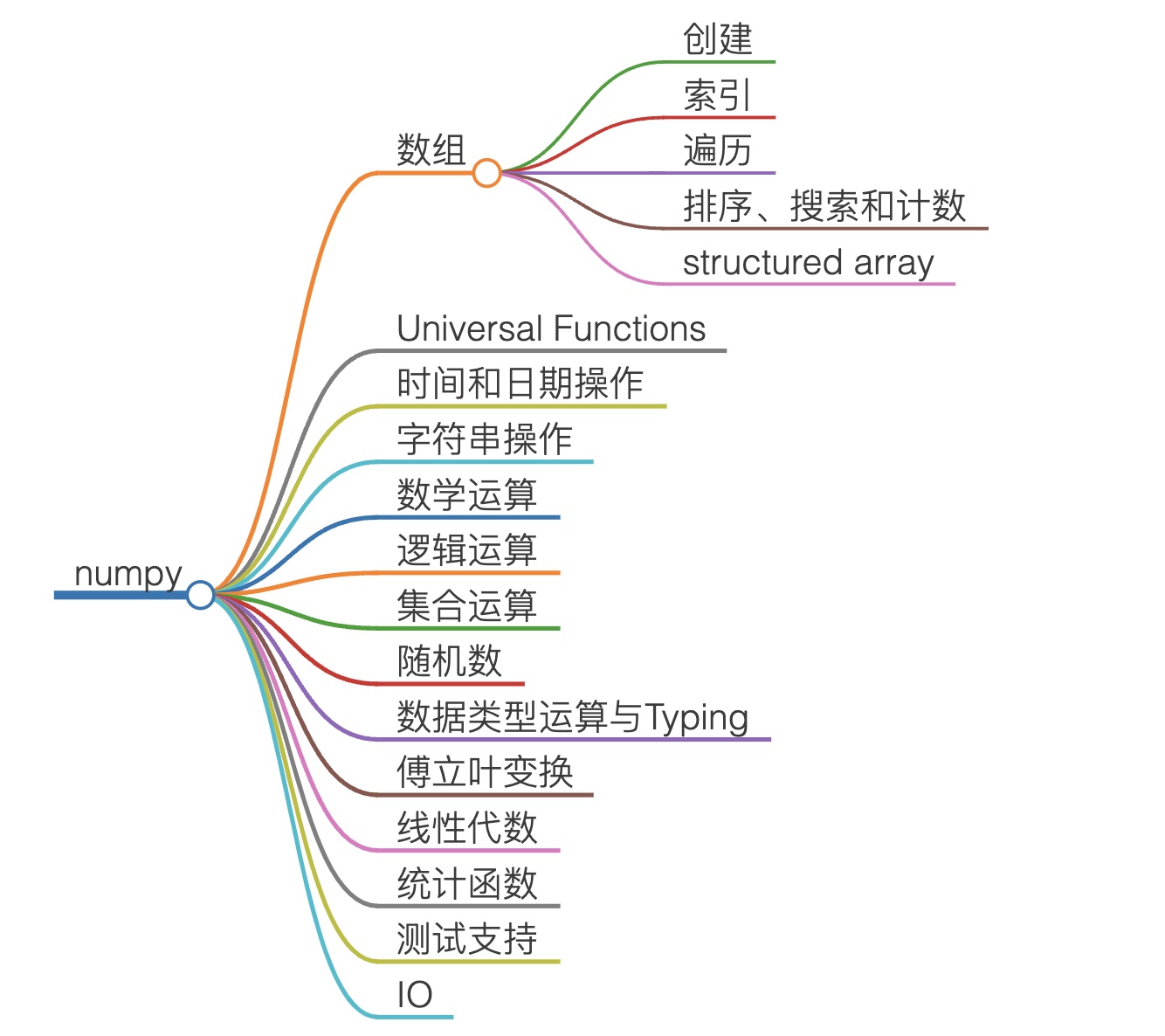
一开始,Numpy 的数组只能存放同质的元素,即元素必须有相同的数据类型。但对表格类数据而言,它们往往是由一条条记录组成的,而这些记录,又是由不同数据类型的数据组成的。
如何做到在Numpy中也能处理大规模的表格数据呢?
为了满足这种需求,Numpy 扩展出一种名为 Structured Array 的数据格式。它是一种 一维数组,每一个元素都是一个命名元组。
我们可以这样声明一个 Structured Array:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | import numpy as np
import datetime
dtypes = [
("frame", "O"),
("code", "O"),
("open", "f4"),
("high", "f4"),
("low", "f4"),
("close", "f4")
]
secs = np.array (
[
(datetime.date (2024, 3, 18), "600000", 8.9, 9.1, 8.8, 9),
(datetime.date (2024, 3, 19), "600000", 8.9, 9.1, 8.8, 9),
], dtype = dtypes
)
|
在这个数据结构中,共有 6 个字段,它们的名字和类型通过 dtype 来定义。这是一个 List [Tuple] 类型。在初始化数据部分,它也是一个 List [Tuple]。
Warning
初学者很容易犯的一个错误,就是使用 List [List] 来初始化 Numpy Structured Array,而不是 List [Tuple] 类型。这会导致 Numpy 在构造数组时,对应不到正确的数据类型,报出一些很奇怪的错误。
比如,下面的初始化是错误的:
| secs = np.array ([
[datetime.date (2024, 3, 18), "600000", 8.9, 9.1, 8.8, 9],
[datetime.date (2024, 3, 19), "600000", 8.9, 9.1, 8.8, 9]
], dtype=dtypes)
|
这段代码会报告一个难懂的 "Type Error: float () argument must be a string or ..."
我们使用上一节学过的 inspecting 方法来查看 secs 数组的一些特性:
| print (f"secs 的维度是 {secs.ndim}")
print (f"secs 的 shape 是 {secs.shape}")
print (f"secs 的 size 是 {secs.size}")
print (f"secs 的 length 是 {len (secs)}")
print (f"secs [0] 的类型是 {type (secs [0])}")
print (f"secs [0] 的维度是 {secs [0].ndim}")
print (f"secs [0] 的 shape 是 {secs [0].shape}")
print (f"secs [0] 的 size 是 {secs [0].size}")
print (f"secs [0] 的 length 是 {len (secs [0])}")
|
可以看出,secs 数组是 一维数组,它的 shape (2,) 也正是一维数组的 shape 的表示法。前一节还介绍过这几个属性的关系,大家可以自行验证下是否仍然得到满足。
Tip
这里 size 仍然等于 shape 各元素的取值之积。注意对 secs 而言,它的 size 与 length 是相等的,但对 secs [0] 而言,它的 size 和 length 是不相等的。我们在开发 Zillionare 量化框架时时,遇到过由此产生的一个 bug。
但 secs 的元素类型则是 numpy.void,它在本质上是一个 named tuple,所以,我们可以这样访问其中的任一字段:
| print (secs [0]["frame"])
# 不使用列名(字段名),使用其序号也是可以的
print (secs [0][0])
|
我们还可以以列优先的顺序来访问其中的一个 “单元格”:
| print (secs ["frame"][0])
|
对表格数据,遍历是很常见的操作,我们可以这样遍历:
| for (frame, code, opn, high, low, close) in secs:
print (frame, code, opn, high, low, close)
|
Numpy structured array 在这部分的语法要比 Pandas 的 DataFrame 易用许多。我们在后面介绍 Pandas 时,还会提及这一点。
Warning
修改 cell 值时,索引的先后不能互换:
| data = np.array ([("aaron", "label")], dtype=[("name", "O"), ("label", "O")])
filter = data ["name"] == "aaron"
new_label = "blogger"
data ["label"][filter] = new_label
# this won't change
data [filter]["label"] = new_label
|
这里的最后一行,并不会生效。
我们在上一节介绍定位、查找时,已经接触到了数据比较,比如:arr > 1。它的结果将数组中的每一个元素都与 1 进行比较,并且返回一个布尔型的数组。
现在,我们要扩充比较的指令:
Tip
为什么需要存在判断近似相等的函数?这是因为,数字分为整型和浮点型。凡是带小数点的数字,都可以看成浮点型。许多浮点数不能精确表达,所以它们是不会相等的,只能比较两个浮点数的差值,如果差值的绝对值小于某个可以接受的小数,才能认为这两个数近似相等。
因此,如果我们拿到了个股的收盘价和涨停价,要判断此时个股有没有涨停,就只能用 isclose 来进行比较,而不能使用 equal。
参数 atol 表示绝对误差,表示两个浮点数之间的差值小于这个值,就可以认为这两个数近似相等。
除了判断一个数组中的元素要么都为 True,要么至少一个为 True 之外,有时候我们还希望进行模糊一点的判断,比如,如果过去 20 天中,超过 60% 的是收阳线,此时我们可以用 np.count_nonzero,或者 np.sum 来统计数组中为真的情况:
| np.count_nonzero (returns > 0)
np.sum (returns > 0)
|
在上一节进行比较的示例中,我们都只使用了单个条件。如果我们要按多个条件的组合进行查找,就需要依靠逻辑运算来实现。
在 Numpy 中,逻辑运算既可以通过函数、也可以通过运算符来完成:
Tip
如果你对编程语言不是特别熟悉,就会难以理解这里的布尔运算,但它们在量化中运用非常广泛,并且在后面讲 pandas 时,我们还会遇到
逻辑与 a&b 的含义是, 只有当条件 a 与 b 都为真时,表达式才成立
逻辑或 a|b 的含义是,a 与 b 之中,任何一个为真即成立
逻辑非~b 的含义是,如果 b 为真,则表达式不成立,反之则成立
逻辑异或 a ^ b 的含义是,只有两个不同时才为真。
逻辑运算有什么用呢?比如我们在选股时,有以下表格数据:
上述表格可以用 Numpy 的 Structured Array 来表示为:
| tickers = np.array ([
("APPL", 30.5, 0.1),
("GOOG", 32.3, 0.3),
("TSLA", 900.1, 0.5),
("MSFT", 35.6, 0.05)
], dtype=[("ticker", "O"), ("pe", "f4"), ("mom", "f4")])
|
现在,我们要找出求 PE < 35, 动量 (mom) > 0.2 的记录,那么我们可以这样构建条件表达式:
| (tickers ["pe"] < 35) & (tickers ["mom"] > 0.2)
|
Numpy 会把 pe 这一列的所有值跟 35 进行比较,然后再与 mom 与 0.2 比较的结果进行逻辑与运算,这相当于:
| np.array ((1,1,0,0)) & np.array ((0, 1, 1, 0))
|
在 Numpy 中,True 与 1 的值在做逻辑运算时是相等的;0 与 False 也是。
如果不借助于 Numpy 的逻辑操作,我们就要用 Python 的逻辑操作。很不幸,这必须使用循环。如果计算量大,这将会比较耗时间。
Tip
这里解释下异或操作。它比较拧巴。如果两个操作数取值一样,那么结果为 False;否则为 True,非常不团结。
在量化中使用异或操作的例子仍然最可能来自于选股。比如,如果我们要求两个选股条件,只能有一个成立时,才买入;否则不买入,就可以使用异或运算。
Tip
在多个条件中,投资者为什么会想要只有一个条件成立?这可能是因为他们认为这两个条件可能互相冲突,或者他们想要在两种投资策略之间进行平衡。
在交易中,我们常常要执行调仓操作。做法一般是,选确定新的投资组合,然后与当前的投资组合进行比较,找出需要卖出的股票,以及需要买入的股票。这个操作,就是集合运算。在 Python 中,我们一般是通过 set 语法来实现。
在 Numpy 中,我们可以使用通过以下方法来实现集合运算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | import numpy as np
# 创建两个一维数组
x = np.array ([1, 2, 3, 4, 5])
y = np.array ([4, 5, 6, 7, 8])
# 计算交集
intersection = np.intersect1d (x, y)
print ("Intersection (交集):", intersection)
# 计算并集
union = np.union1d (x, y)
print ("Union (并集):", union)
diff = np.setdiff1d (x, y)
print ("x - y:", diff)
|
此外,我们还可能使用 in1d (a1, a2) 方法来判断 a1 中的元素是否都在 a2 中存在。比如,在调仓换股中,如果当前持仓都在买入计划中,则不需要执行调仓。
Numpy 中数学相关的运算有线性代数运算(当然还有基本代数运算)、统计运算、金融指标运算等等。
线性代数在量化中有重要用途。比如,在现代资产组合理论(MPT)中,我们要计算资产组合收益率及协方差,都要使用矩阵乘法。大家可以参考 投资组合理论与实战 系列文章,下面是其中的一段代码:
| ...
cov = np.cov (port_returns.T)
port_vol = np.sqrt (np.dot (np.dot (weights, cov), weights.T))
|
矩阵乘法是线性代数中的一个核心概念,它涉及到两个矩阵的特定元素按照规则相乘并求和,以生成一个新的矩阵。具体来说,如果有一个矩阵 A 为 m×n 维,另一个矩阵 B 为 n×p 维,那么它们的乘积 C=AB 将会是一个 m×p 维的矩阵。乘法的规则是 A 的每一行与 B 的每一列对应元素相乘后求和。
下面通过一个具体的例子来说明矩阵乘法的过程:
假设我们有两个矩阵 A 和 B:
A=[23 14]
和
B=[12 31]
要计算 AB,我们遵循以下步骤:
取 A 的第一行 (2,3) 与的第一列 (1,3) 相乘并求和得到 C11=[2×1+3×3=11]
同理,取 A 的第一行与 B 的第二列 (2,1) 相乘并求和得到 C12=[2×2+3×1=7]
取 A 的第二行 (1,4) 与 B 的第一列相乘并求和得到 C21=[1×1+4×3=13]
取 A 的第二行与 B 的第二列相乘并求和得到 C22=[1×2+4×1=5]
因此,矩阵 C = AB 为:
C=[111376 ]
与代数运算不同,矩阵乘法不满足交换律,即一般情况下 AB=BA。
在 Numpy 中,我们可以使用 np.dot () 函数来计算矩阵乘法。
上述示例使用 numpy 来表示,即为:
| A = np.array ([[2,3],[1,4]])
B = np.array ([[1,2],[3,1]])
np.dot (A, B)
|
最终我们将得到与矩阵 C 相同的结果。
除此之外,矩阵逆运算 (np.linalg.inv) 在计算最优投资组合权重时,用于求解方程组,特征值和特征向量 (np.linalg.eig, np.linalg.svd) 在分析资产回报率的主成分,进行风险分解时使用。
常用的统计运算包括:
np.percentile 与 np.quantile 功能相同,都是用于计算分位数。
两者在参数上略有区别。当我们对同一数组,给 quantile 传入分位点 0.25 时,如果给 percentile 传入分位点 25 时,两者的结果将完全一样。也就是后者要乘以 100。在量化交易中,quantile 用得可能会多一些。
Tip
在 pandas 中存在 quantile 函数,但没有 percentile 函数。
np.percentile(或者 np.quantile)的常见应用是计算 25%, 50% 和 75% 的分位数。用来绘制箱线图(Boxplot)。
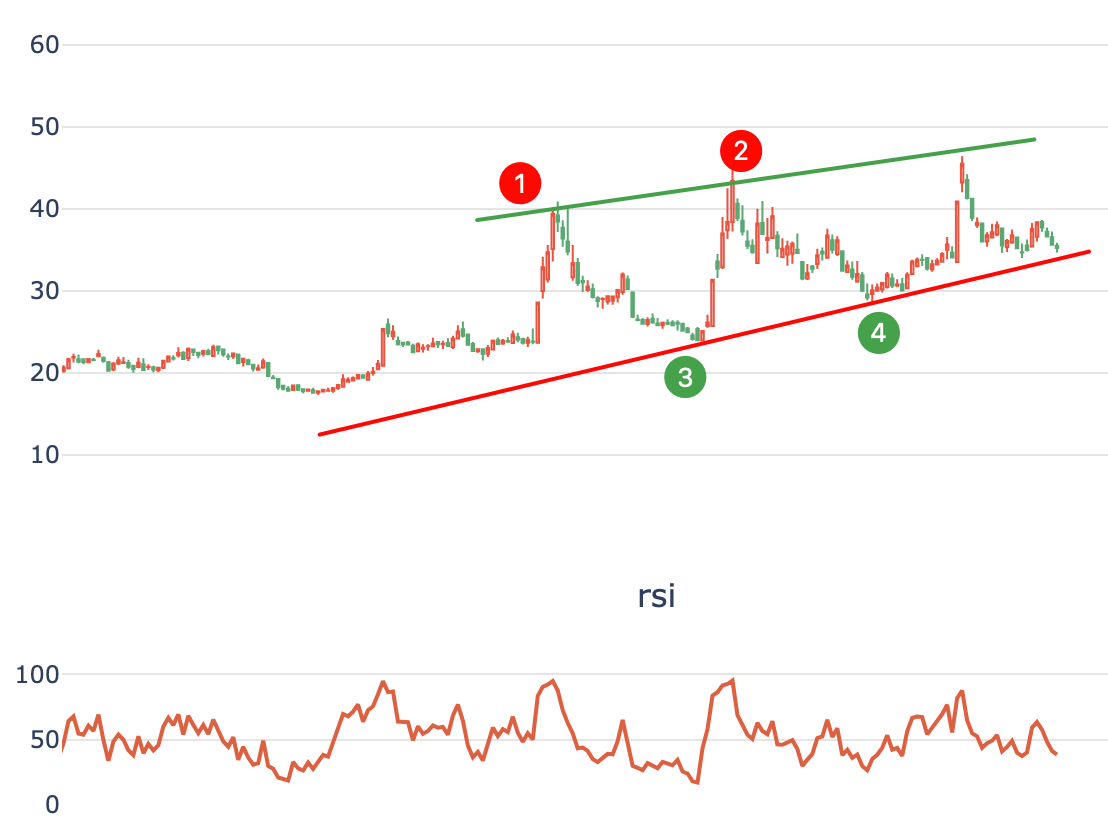
此外,我们也常用它来选择自适应参数。比如,在 RSI 的应用中,一般推荐是低于 20(或者 30)作为超卖,此时建议买入;推荐是高于 80(或者 70)作为超买,此时建议卖出。但稍微进行一些统计分析,你就会发现这些阈值并不是固定的。如果我们以过去一段时间的 RSI 作为统计,找出它的 95% 分位作为卖点,15% 作为买点,往往能得到更好的结果。
有一些常用的量化指标的计算,也可以使用 Numpy 来完成,比如,计算移动平均线,就可以使用 Numpy 提供的 convolve 函数。
| import numpy as np
def moving_average (data, window_size):
return np.convolve(data,
np.ones(window_size)/window_size,
'valid')
|
当然,很多人习惯使用 talib,或者 pandas 的 rolling 函数来进行计算。convolve(卷积)是神经网络 CNN 的核心,正是这个原因,我们这里提一下。
np.convolve 的第二个参数,就是卷积核。这里我们是实现的是简单移动平均,所以,卷积核就是一个由相同的数值组成的数组,它们的长度就是窗口大小,它们的和为 1。
如果我们把卷积核替换成其它值,还可以实现 WMA 等指标。从信号处理的角度看,移动平均是信号平滑的一种,使用不同的卷积核,就可以实现不同的平滑效果。
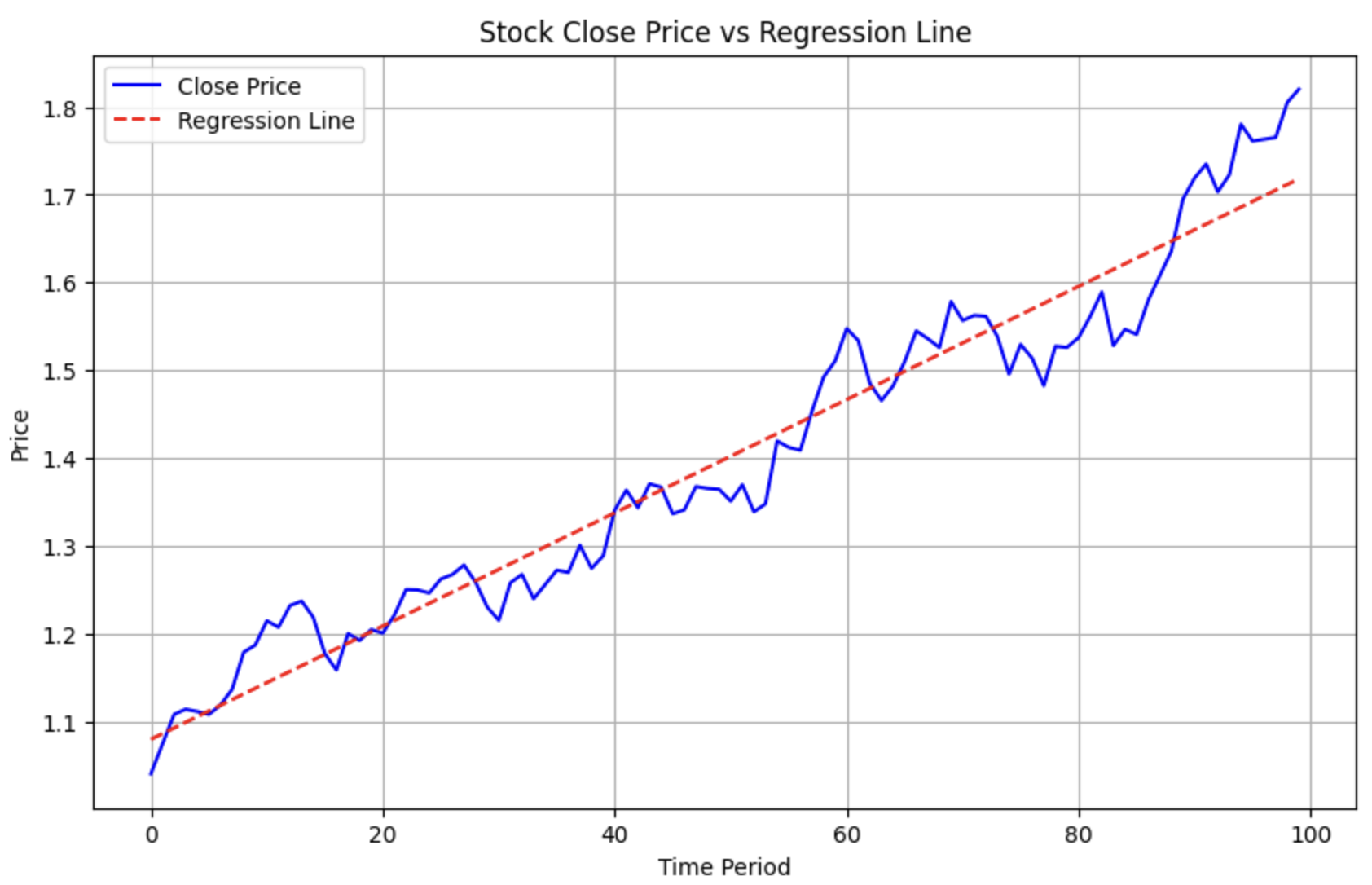
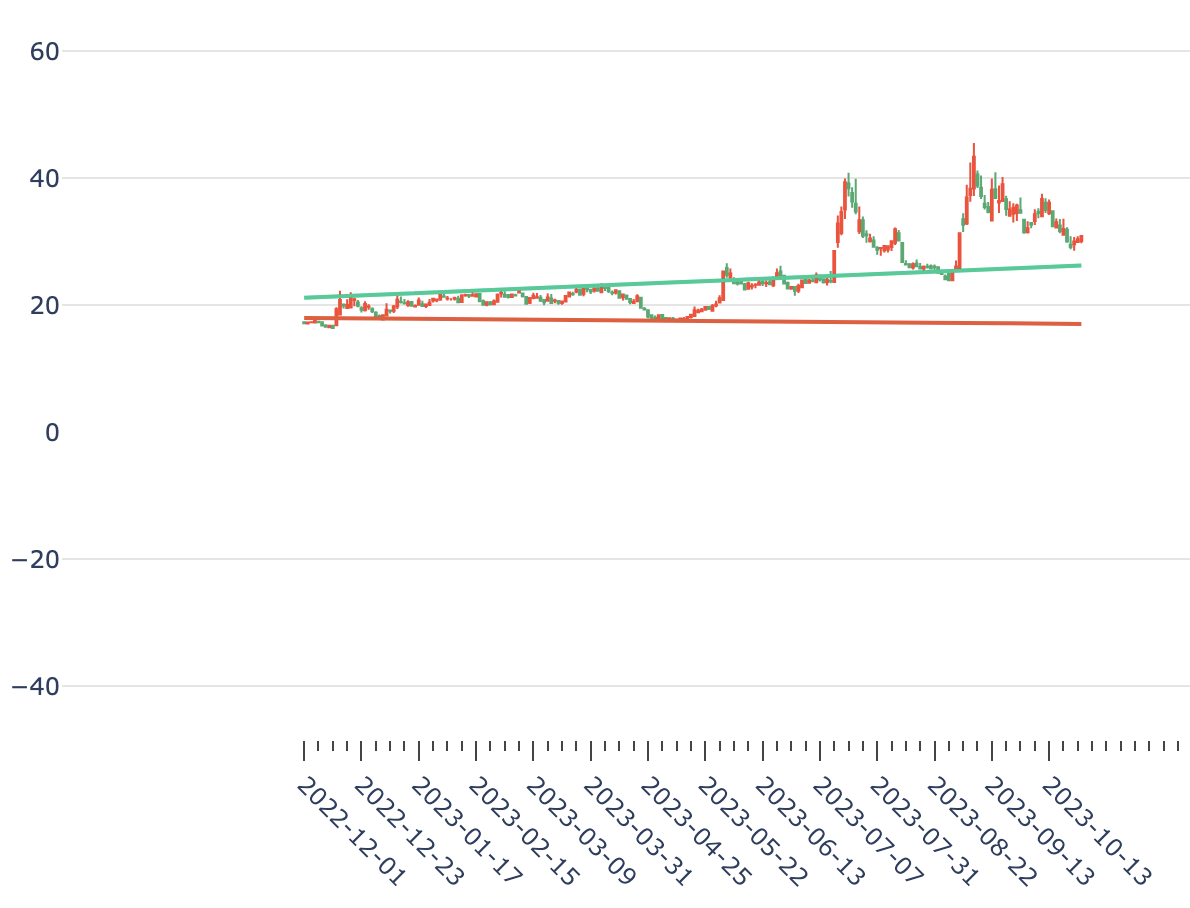
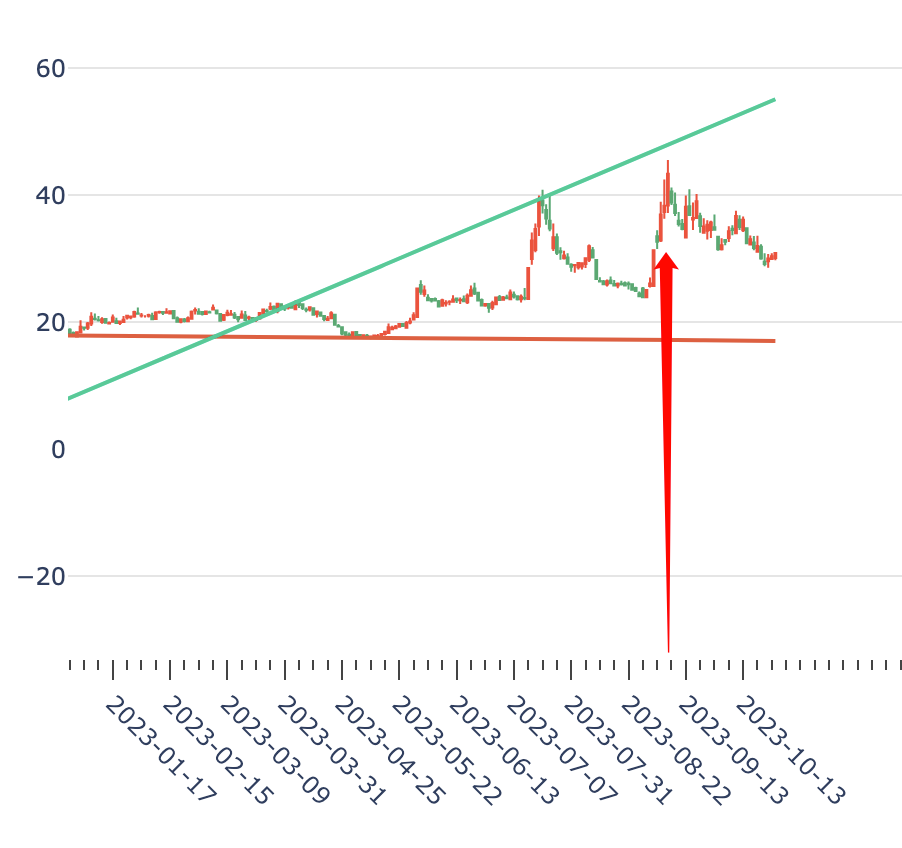
在量化中,还有一类计算,这里也提一下,就是多项式回归。比如,某两支股票近期都呈上升趋势,我们想知道哪一支涨得更好?这时候我们就可以进行多项式回归,将其拟合成一条直线,再比较它们的斜率。
下面的代码演示了如何使用 Numpy 进行多项式回归。
| import numpy as np
import matplotlib.pyplot as plt
returns = np.random.normal (0, 0.02, size=100)
alpha = 0.01
close = np.cumprod (1 + returns + alpha)
a, b = np.polyfit (np.arange (100), close, deg=1)
# 使用 a, b 构建回归线的 y 值
regression_line = a * np.arange (100) + b
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | # 绘制原始的 close 曲线
plt.figure (figsize=(10, 6))
plt.plot (close, label='Close Price', color='blue')
# 绘制回归线
plt.plot (regression_line, label='Regression Line', color='red', linestyle='--')
# 添加图例、标题和坐标轴标签
plt.title ('Stock Close Price vs Regression Line')
plt.xlabel ('Time Period')
plt.ylabel ('Price')
plt.legend ()
# 显示图表
plt.grid (True)
plt.show ()
|
这将生成下图:
题图: Photo by Steve Harvey on Unsplash