投资组合理论与实战(3) - 优化算法

---

Table of Content

寻找给定收益率下的最小波动率，或者给定波动率下的最大夏普率，这实际上是一类常见的优化问题，即：

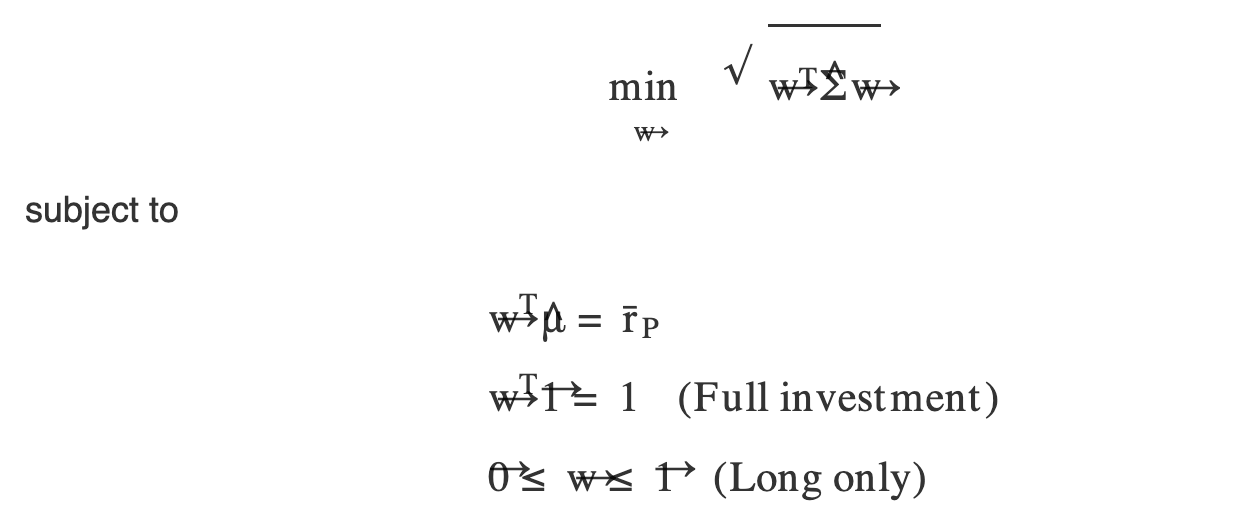
我们可以使用 Scipy.optimize工具库来求解类似问题。

scipy.optimize包的主要功能 * SciPy Optimize提供最小化(或最大化)目标函数的功能，可能存在约束。 * 它包括解决非线性问题(支持局部和全局优化算法) ，线性规划，约束和非线性最小二乘，根寻找和曲线拟合。 * 当我们需要优化输入函数的参数时，scipy.optimize包含很多有用的方法，并可以处理不同种类的函数

它提供以下方法： * minimize_scalar( )：使一个变量最小化 * minimize( )：使多个变量最小化 * curve_fit( )：寻找最优曲线，适合a set of data * root_scalar( )：求一个变量的零点 * root( )：求多个变量的零点 * linprog( )：在线性等式和不等式的约束下，最小化线性目标函数

在这些方法中，我们主要介绍minimize_scalar和minimize。

minimize_scalar

有一类问题，比如解方程，它的解是一个数字，此时就可以用 minimize_scalar 方法来求解。

例如，我们的函数为：

\(y=3x^4-2x+1\)

minimize_scalar( )就是帮助我们找到函数最小值(y最小)时精确的坐标。通俗地说，就是解方程。

from scipy.optimize import minimize_scalar

def objective_function(x):
    return 3 * x ** 4 - 2 * x + 1
# 定义需要求解的函数

res = minimize_scalar(objective_function)
# 求出函数的最小值

print(res)

我们重点解释一下输出结果，这将在后面继续使用：

 message: 
          Optimization terminated successfully;
          The returned value satisfies the termination criteria
          (using xtol = 1.48e-08 )
 success: True
     fun: 0.17451818777634331
       x: 0.5503212087491959
     nit: 12
    nfev: 15

这里的fun是函数值，x是变量值，如果我们把x的值代入到公式 \(3*x^4-2*x+1\)，我们会得得到0.17,即fun的值。

要注意，不是所有情况都能进行优化求解的。比如，\(y=x^3\)没有最小值，如果我们对它求解，会导致overflowerror.

另外的情况是，存在多个最小值的情况，此时minimize_scalar不能保证找到函数的全局最小值。

我们以\(y=x^4-x^2\)为例，它存在多个最小值，minimize_scalar ()不能保证找到函数的全局最小值。我们尝试一下：

from scipy.optimize import minimize_scalar
# help(minimize)

def objective_function(x):
    return x**4 - x**2

res = minimize_scalar(objective_function)
res

我们将得到如下结果：

 message: 
          Optimization terminated successfully;
          The returned value satisfies the termination criteria
          (using xtol = 1.48e-08 )
 success: True
     fun: -0.24999999999999994
       x: 0.7071067853059209
     nit: 11
    nfev: 14

这样求解出来的方程的根是0.707。但我们知道，该方程至少还有一个-0.707的根，因此， minimize_scalar默认情况下，是无法找出全部的根的。但我们可能通过设定参数，来控制用于优化的求解器。一共有三种设定方式： * brent:布伦特算法，也是该函数的默认算法 * golden:黄金分割算法，根据已有研究，该方式效果略差于brent * bounded:布伦特算法的“有界实现”

brent和golden属于bracket：这是一个由两个或三个元素组成的序列，它提供了对最小区域边界的初始猜测。但是，这些求解器并不保证所找到的最小值将在此范围内。

bounded属于bounds：这是一个两个元素的序列，严格限制搜索区域的最小值。因此当最小值在已知范围内时，限制搜索区域才是有用的。这个概念我们在后面还将进一步接触。我们来看使用bounds方式的例子：

# 当我们采用bounds方式限定时
res = minimize_scalar(objective_function, method='bounded', bounds=(-1, 0))
res

现在，我们求解的x将落在区间(-1,0)之间，我们因此得到：

 message: Solution found.
 success: True
  status: 0
     fun: -0.24999999999998732
       x: -0.707106701474177
     nit: 10
    nfev: 10

这次我们得到了期望中的负数解。

不过，最佳资产组合的求解要比这个复杂，我们必须使用另一个方法，即minimize方法，具体优化算法则是最小顺序二乘法。

使用 minimize 方法

在前面的示例中，我们了解了目标函数、bounds限定方式以及求解结果 OptimizeResults对象，特别是它的fun属性和x属性。接下来我们还要介绍约束（constraints）概念。掌握这些概念之后，就基本掌握了凸优化。

我们先来看minimize方法的签名：

scipy.optimize.minimize(fun, 
                        x0, 
                        args=(), 
                        method=None, 
                        jac=None, 
                        hess=None, 
                        hessp=None, 
                        bounds=None, 
                        constraints=(), 
                        tol=None, 
                        callback=None, 
                        options=None)

我们重点介绍跟本章主题相关的参数，主要是fun, x0, method, bounds和constraints。

这里的fun是指目标函数，之前我们已经接触过这个概念。如果目标函数需要传入参数，则它的参数将通过args来传入。

优化方法使用一系列迭代来进行求解满足目标函数的物理量x，它需要从一组初始值开始。x0就是我们提供给优化方法的初始值。它的最终结果，将通过OptimalResult.x来传递回来。

对不同的问题，有不同的优化方案。minimize方法支持了大约14种优化方案，此外还允许你自定义优化算法。在进行优化求解之前，我们一般需要指定一种优化算法。

bound和constraints参数，我们将我们结合有效前沿求解问题，来介绍如何使用。同时，也讲解其它参数的使用。

我们先来构建一个最小方差的投资组合。我们先来定义目标函数：

def portfolio_sd(w):
    return np.sqrt(np.transpose(w) @ (returns.cov() * 253) @ w)

注意这里的常数253。我们使用它来将收益进行年化。这是一种粗略但简单的方法。接下来，我们需要定义约束条件，以实现“在某个收益率时，波动最小”这个需求。首先，我们要定义年化收益率：

def portfolio_returns(w):
    return (np.sum(returns.mean() * w)) * 253

然后，我们来定义约束。minimize方法要求通过dict来传入约束条件。它支持两种表达式，即'eq'和'ineq'。

constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})

这里定义了一个约束。'eq'表明'fun'指向的表达式必须等于零。'fun'的值可以是lambda表达式，也可以是常规函数。这个lambda表达式的含义是，权重x的各项之和，必须等于1（这是显然的！）。需要指出的是，这里的fun并不是minimize首个参数的fun，而是一种约束条件。它的参数是惟一的，即minimize的第二个参数x0所代表的那个物理量。

我们也可以指定一个'ineq'表达式，这意味着fun指向的表达式或者函数，其返回值必须大于零。

constraints = ({
    'type': 'ineq', 'fun': lambda x: x[0],
})

同样的，这里的x是传入的是在迭代过程中的、我们要求解的满足目标函数的物理量。在最佳投资组合求解示例中，它是各项资产的权重。因此，x[0]就表示第0号资产的权重必须大于0。这是我们在本例中，另外一个约束。

实际上，我们对资产权重的约束是[0,1]，上述表达式只能完成一半目标。正确的做法是使用bounds：

x0 = np.ones(len(stocks)) / len(stocks)
bounds = tuple((0,1) for _ in x0)

有多少个资产，我们就要建立多少个这样的有界约束。

现在，我们把所有的材料放在一起“煮”：

from scipy.optimize import minimize

res = minimize(
    fun = portfolio_sd,
    x0 = x0,
    method = 'SLSQP',
    bounds = bounds,
    constraints = constraints
)
res

这样我们得到以下结果：

 message: Optimization terminated successfully
 success: True
  status: 0
     fun: 0.14842169691096224
       x: [ 2.500e-01  2.500e-01  2.500e-01  2.500e-01]
     nit: 1
     jac: [ 0.000e+00  0.000e+00  0.000e+00  0.000e+00]
    nfev: 5
    njev: 1

nit表明函数运行的次数，由于我们并没有加上收益率约束，所以这个函数实际上什么也没干，我们从x的值可以看出这一点。

我们加上收益率约束再试一次:

constraints = (
    {'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
    {'type': 'eq', 'fun': lambda x: portfolio_returns(x) - 0.1}
)

res = minimize(
    fun = portfolio_sd,
    x0 = x0,
    method = 'SLSQP',
    bounds = bounds,
    constraints = constraints,
    options = dict(disp=True)
)
res

Info

注意我们在这里加了一个options参数。通过它可以进一步揭示迭代过程。

这次仍然只迭代一次就结束了，但权重x的值变了。我们用它求解出来权重值看一下，得到的组合收益是否为0.1：

portfolio_returns(res.x)

返回结果的确是0.1，说明求解过程正确。同时，只迭代一次就得到正确结果，这个效率也令人满意。

现在，如果我们再来求解有效前沿，应该怎么做？

显然，我们应该先找出该组合的理论最大、最小收益，然后在这个区间里进行线性划分，将每一个收益点作为约束条件，求解出对应的资产分配权重，然后再依据这个权重分配，计算其它指标，比如sharpe。

组合的理论最大收益是把所有的仓位都分配给表现最好的股票得到的；反之，如果所有的仓位都分配给表现最差的资产，则我们会得到最小收益。

returns表记录了每一个标的的daily return，我们可以用下面的方法来求每一个标的的年化：

all_annual_returns = (1 + returns.mean()) ** 253 - 1
best = np.max(all_annual_returns)
worst = np.min(all_annual_returns)
print(best, worst)

我们得到资产组合的最大收益是20%，最差收益是-28%。现在我们来求解有效前沿，这一次，我们给足完整的代码：

sharpes = []
vols = []
weights = []
rets = []

all_annual_returns = (1 + returns.mean()) ** 253 - 1
best = np.max(all_annual_returns)
worst = np.min(all_annual_returns)

x0 = np.ones(len(stocks)) / len(stocks)
constraints = (
    {'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
    {'type': 'eq', 'fun': lambda x: portfolio_returns(x) - target}
)

# 这一次，我们要求每个标的至少分配1%的权重
bounds = tuple((0.01, 1) for _ in stocks)

for target in np.linspace(worst, best, 100):
    res = minimize(
        fun = portfolio_sd,
        x0 = x0,
        method = 'SLSQP',
        bounds = bounds,
        constraints = constraints
    )

    vols.append(res.fun)
    weights.append(res.x)
    rets.append(target)

    # 计算sharpe
    sharpe = sharpe_ratio(returns.dot(res.x))
    sharpes.append(sharpe)

# 绘制图形
plt.scatter(vols, rets, c=sharpes, cmap='RdYlBu')
pos = np.argmax(sharpes)
plt.colorbar(label='Sharpe Ratio')
plt.scatter(vols[pos], rets[pos], marker='*', s=80, color='red')

运行总共花了11秒。看上去比运行5000次蒙特卡洛模拟还要慢，但是，它是几乎涵盖了可能的每一种组合。这是5000次蒙特卡洛模拟做不到的。

代码中有一些地方需要进一步解释。我们在前面讲解过lambda表达式np.sum(x) - 1中x的来源。您应该注意到，我们并没有在任何地方声明它。实际上，它只是一个形式参数，您可以使用任何变量名，minimize方法都会将迭代中的根变量传递给它 -- 在这个例子中，就是求解中的权重矩阵。然而，另一个约束条件：

    lambda x: portfolio_returns(x) - target

这里的target来自何处？它的值又是如何传递的呢？实际上，我们必须提前使用这个变量，但只到第19行，我们才在for循环中声明这个变量，并且将最新的值传递给了lambda表达式。

还有一个浮点数问题。即'eq'表达式，它的结果是要跟0相比较的。但是由于各种浮点误差，理论上等于零的表达式，在计算机看来可能不等于0。比如， 在 portfolio_returns(x) - target < 0.001的时候，其实我们已经可以认为这个优化到位了，但minimize会一直寻找到这个差值小于1e-7为止。

我们可以通过对portfolio_returns的返回值和target进行取整（比如，小数点后3位）来加快计算速度，但当我们这样做的时候，要注意由于不知道minimize内部实现时的步长，有可能导致优化失败。

如果我们有进一步加快速度的需要，可以考虑使用scipy.optimize包中的另外一个方法，fmin_slsqp:

    scipy.optimize.fmin_slsqp(
        func, 
        x0, 
        eqcons=(), 
        bounds=(), 
        acc=1e-06, 
        iprint=1, 
        disp=None, 
        full_output=0, 
        epsilon=1.4901161193847656e-08, 
        callback=None)

它提供了acc和epsilon这两个参数，应该跟我们这里的思路是一致的。它的默认值也可能就是minimize内部实现时的默认值。它也是顺序最小二乘法优化方法。只不过文档比较少，也没有示例。这里就不展开了，供大家参考。

我们已经探讨了资产组合理论的方方面面，并且学会了如何使用蒙特卡洛方法和凸优化方法来求解约束条件下的最佳资产组合。

但是，在实际投资中，我们遇到的情况会更复杂，并不是我们上面介绍的方法就可以完全 cover 的。比如，我们可能会遇到以下情况（需求）：

1. 在均值、方差模型中，我们把收益率为正的波动也计入进来了。但实际上，我们可能只关注收益率为负的那部分波动 -- 这正是策略评估指标 - sortino 指标被发明出来的原因。这只是我们优化模型的路径之一。我们可能还希望实现各种新的发现，但时间和能力可能都不允许。
2. 迄今为止，我们只考虑了权重为正的情况。也就是，我们只允许做多。但实际上，通过做空来对冲风险的需求也是存在的。如果我们要允许做空，又该如何？
3. 尽管我们的标的池里有 500 个标的，但如果必须将投资组合限制为最多 10 项资产，又该如何处理？这可不仅仅是从中挑选 10 支标的再把前面的流程走一遍那么简单。毕竟，该如何从 500 个标的的标的池里，选出最佳的 10 支呢？
4. 如果我们希望进行行业中性化呢（即每个行业均衡配置资产，而不要出现资产主要配置在某一个行业内的情况）？