strategy »
『译研报03』Z变换改造均线,一个12年前的策略为何仍能跑赢大盘?
传统移动平均线(MA)是技术分析中常用的趋势跟踪指标,通过对股票价格或指数在一定天数内的平均值进行计算,以刻画其变动方向。MA 的计算天数越多,其平滑性越好,但随之而来的时滞(延迟)影响也越严重。这意味着 MA 指标在跟踪趋势时容易出现“跟不紧”甚至“跟不上”的情况,平滑性和延迟性成为其不可避免的矛盾。
低延迟趋势线(LLT)的构造借鉴了信号处理理论中的滤波方法。传统的 EMA 指标被视为一阶低通滤波器,但其滤波效果相对较差,通带和阻带间的过渡带太长。LLT 通过设计二阶滤波器来优化滤波效果,实现了对信号高频部分的有效过滤,同时保留了低频部分的强度。与 MA 和 EMA 均线相比,LLT 大幅降低了延迟,同时兼顾了趋势线的平滑性,从而克服了传统 MA 指标在跟踪趋势时的滞后问题。
本文取材于广发证券-《低延迟趋势线与交易择时》一文。原文仅回测到2013年。我们在此基础上回测到2024年底,发现它在多空组合时,仍有很好的表现(上证夏普1.33)。
策略档案之LLT
LLT
Benchmark
Strategy
Start Period
2013-01-04
2013-01-04
End Period
2024-12-31
2024-12-31
Cumulative Return
47%
345%
CAGR﹪
2%
9%
Sharpe
0.27
1.33
传统均线系统
为了对比,我们先给出传统均线的定义及图形。
移动平均(Moving Average)线,其算法为:
\(MA(n) = \frac{1}{n}\sum^{n-1}_{i=0}price(T-i)\)
其中 price 一般选择收盘价,MA(n) 即为 T 日的 n 日均线指标。对于 MA 指标,n 越大,趋势线的平滑性越好。
基于移动均线,我们可以实现一个简单的趋势跟随策略。信号的判断方式是看移动平均线的切线。如果切线斜率向上,则多头持有;如果切线斜率向下,则多头卖出。
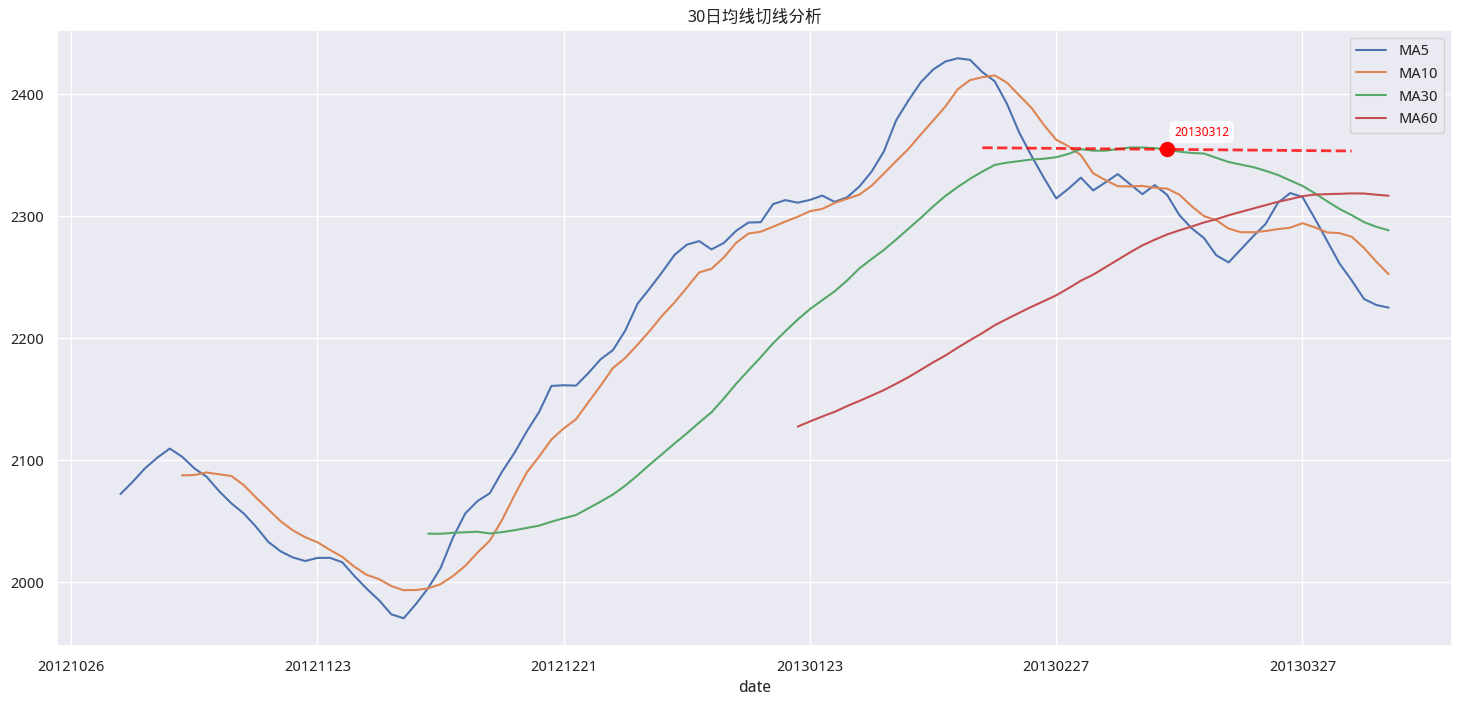
下面的代码演示了 5, 10, 30 和 60 日均线。其中 30 日均线被称为生命线。最后的绘图中,显示了 30 日均线上,切线由正转负的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73 def get_price ( symbol , start_date , end_date ):
pro = pro_api ()
price_df = pro . index_daily (
ts_code = symbol ,
start_date = start_date . strftime ( "%Y%m %d " ),
end_date = end_date . strftime ( "%Y%m %d " ),
)
price_df = (
price_df . rename ({ "trade_date" : "date" , "ts_code" : "asset" }, axis = 1 )
. sort_values ( "date" , ascending = True )
. set_index ( "date" )
)
return price_df [[ "close" ]]
start = datetime . date ( 2012 , 10 , 26 )
end = datetime . date ( 2013 , 4 , 9 )
price_df = get_price ( "000001.SH" , start , end )
for i in [ 5 , 10 , 30 , 60 ]:
price_df [ f "MA%d" % i ] = price_df [ "close" ] . rolling ( i ) . mean ()
# 计算生命线趋势拐点
price_df [ "slope_30_5" ] = price_df [ "MA30" ] . rolling ( 5 , min_periods = 5 ) . apply ( lambda y : np . polyfit ( np . arange ( 5 ), y , 1 )[ 0 ])
price_df [ "slope_30_5" ] = price_df [ "slope_30_5" ] . fillna ( 0 )
signs = np . sign ( price_df [ "slope_30_5" ])
sign_changes = signs * signs . shift ( 1 ) == - 1
revert_dates = price_df . index [ sign_changes ]
print ( "找到的反转日期:" , [ i for i in revert_dates ])
# 在现有图表上添加切线
cols = [ "MA5" , "MA10" , "MA30" , "MA60" ]
ax = price_df [ cols ] . plot ( figsize = ( 18 , 8 ), title = '30 日均线切线分析' )
# 切线长度
tangent_length = 15
for dt in revert_dates :
# 获取该位置的 MA 值和斜率
ma_value = price_df . loc [ dt , 'MA30' ]
slope = price_df . loc [ dt , 'slope_30_5' ]
i = price_df . index . get_loc ( dt )
# 计算切线范围
start_idx = max ( 0 , i - tangent_length )
end_idx = min ( len ( price_df ), i + tangent_length + 1 )
# 计算切线坐标
x_offset = np . arange ( start_idx - i , end_idx - i )
y_tangent = ma_value + slope * x_offset
tangent_dates = np . arange ( start_idx , end_idx )
# 绘制切线
color = 'green' if slope > 0 else 'red'
linestyle = '-.' if slope > 0 else '--'
ax . plot ( tangent_dates , y_tangent ,
color = color , linestyle = linestyle , linewidth = 2 , alpha = 0.8 )
# 标记切点
ax . scatter ( i , ma_value , color = color , s = 100 , zorder = 5 )
ax . annotate ( dt ,
xy = ( i , ma_value ),
xytext = ( 5 , 10 ), textcoords = 'offset points' ,
fontsize = 9 , color = color ,
bbox = dict ( boxstyle = 'round,pad=0.3' , facecolor = 'white' , alpha = 0.8 ))
plt . show ()
在该图中,绿色线为30日线。红点处,30日均线斜率由正转负,即为卖出信号。我们看到,通过 30 日均线的趋势跟随,可以捕捉到大的波段行情。但是,当趋势线提示我们该下车时,已经离行情高点下降不少。但如果使用 5 日均线这种短一点的均线,又会导致频繁发出信号,增加交易成本的情况。
这个结果表明,传统均线存在窗口小时,均线不平滑,趋势线切线上下抖动现象严重;窗口大时,均线平滑性好,但滞后性较强的问题。
Tip
寻找切线反转点(即切线斜率由正变负,或者由负变正)时,比较有技巧。这个技巧在很多场合下都会遇到:
price_df [ "slope_30_5" ] = price_df [ "slope_30_5" ] . fillna ( 0 )
signs = np . sign ( price_df [ "slope_30_5" ])
sign_changes = signs * signs . shift ( 1 ) == - 1
revert_dates = price_df . index [ sign_changes ]
如何解决传统均线在延迟和平滑上,存在鱼与熊掌不可兼得的矛盾?
LLT 均线
研报在 LLT 均线的原理及推导上介绍得比较深入细致。但是,要理解 LLT,需要有 Z 变换等基础,我们简单解释如下:
\[\frac{LLT(z)}{price(z)} = \frac{(\alpha-\alpha^2/4) + (\alpha^2/2)z^{-1} - (\alpha-3\alpha^2/4)z^{-2}}{1-2(1-\alpha)z^{-1} + (1-\alpha)^2z^{-2}}\]
这是一个所谓的Z域上的公式,我们需要按相应的规则,变换为时域公式。它的变换规则是:
上式是一个二阶 IIR 滤波器的传递函数。要得到时域递推公式,需要将分子分母都乘以分母的表达式,使分母变为 1(即左边只剩 LLT(z)),右边是分子的多项式与 price(z) 的卷积:
\(\(LLT(z) \cdot [1-2(1-\alpha)z^{-1} + (1-\alpha)^2z^{-2}] = price(z) \cdot [(\alpha-\alpha^2/4) + (\alpha^2/2)z^{-1} - (\alpha-3\alpha^2/4)z^{-2}]\) \)
展开后,按 z 变换的性质,将 z{-1}、z 分别对应到时域的 t-1、t-2 期:
\(\(LLT_t - 2(1-\alpha)LLT_{t-1} + (1-\alpha)^2LLT_{t-2} = (\alpha-\alpha^2/4)price_t + (\alpha^2/2)price_{t-1} - (\alpha-3\alpha^2/4)price_{t-2}\) \)
移项得到递推公式:
\(\(LLT_t = (\alpha-\alpha^2/4)price_t + (\alpha^2/2)price_{t-1} - (\alpha-3\alpha^2/4)price_{t-2} + 2(1-\alpha)LLT_{t-1} - (1-\alpha)^2LLT_{t-2}\) \)
变换后,我们最终得到的公式为:
\[
y_t = (\alpha-\alpha^2/4)x_t + (\alpha^2/2)x_{t-1} - (\alpha-3\alpha^2/4)x_{t-2} + 2(1-\alpha)y_{t-1} - (1-\alpha)^2y_{t-2}
\]
可以看到,最终公式是一个递归函数,这里的\(y_t\) 即为我们要求的LLT,它由前两期的LLT与最近三期的价格、以及一个\(\alpha\) 参数共同决定。
它的实现代码是:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def calculate_llt ( prices , alpha = 0.05 ):
"""
计算LLT (Linearly Weighted Least Squares Triangular) 均线
参数:
prices (array-like): 价格序列
alpha (float): 平滑系数,范围(0,1),值越小均线越平滑,滞后性越大
返回:
array: LLT均线序列
"""
n = len ( prices )
llt = np . zeros ( n )
# 初始化前两个值
if n >= 1 :
llt [ 0 ] = prices [ 0 ]
if n >= 2 :
llt [ 1 ] = prices [ 1 ]
# 计算系数
a1 = alpha - ( alpha ** 2 ) / 4
a2 = ( alpha ** 2 ) / 2
a3 = alpha - 3 * ( alpha ** 2 ) / 4
a4 = 2 * ( 1 - alpha )
a5 = - ( 1 - alpha ) ** 2
# 递归计算LLT
for t in range ( 2 , n ):
llt [ t ] = a1 * prices [ t ] + a2 * prices [ t - 1 ] - a3 * prices [ t - 2 ] + a4 * llt [ t - 1 ] + a5 * llt [ t - 2 ]
return llt
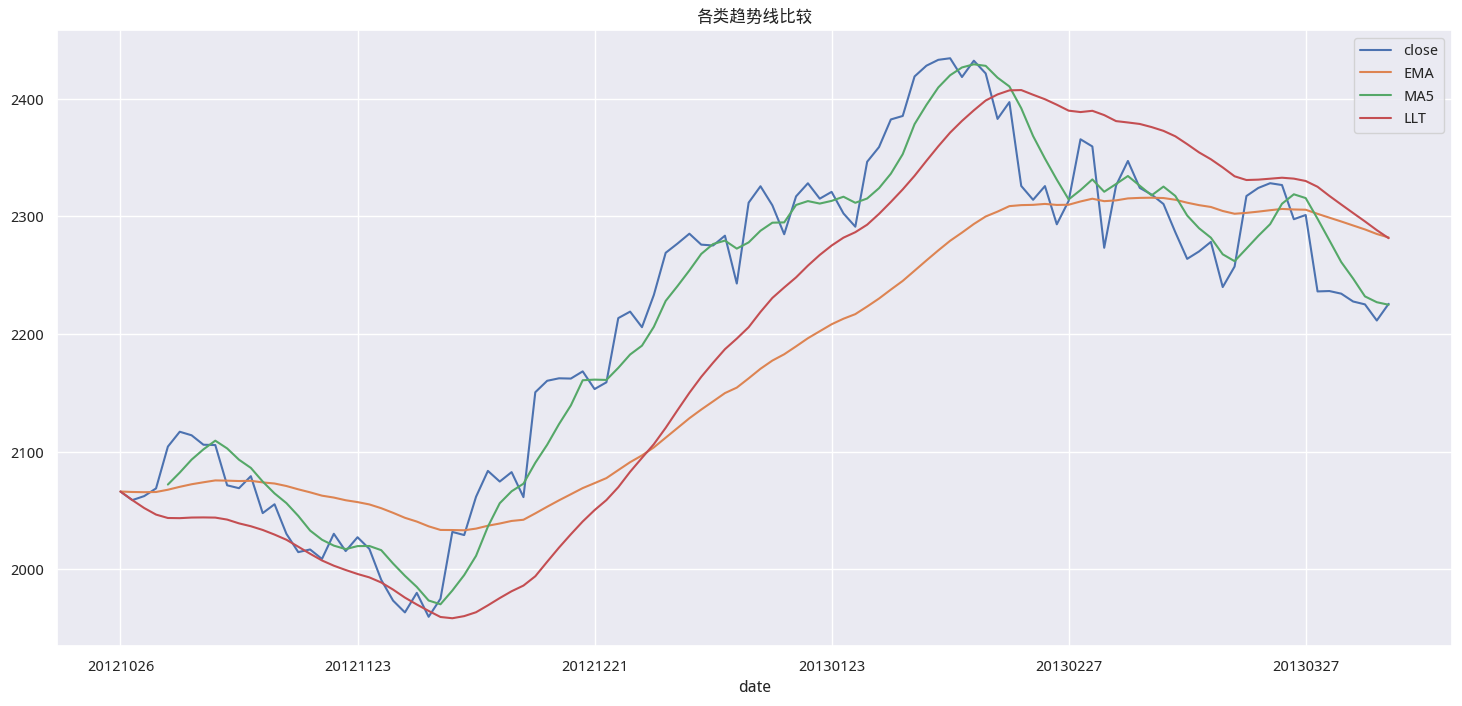
下面,我们对比一下EMA, 5日均线以及LLT均线:
price_df = get_price ( "000001.SH" , start , end )
price_df [ 'EMA' ] = price_df [ 'close' ] . ewm ( alpha = 0.05 , adjust = False ) . mean ()
price_df [ 'MA30' ] = price_df [ 'close' ] . rolling ( 30 ) . mean ()
price_df [ 'LLT' ] = calculate_llt ( price_df [ 'close' ], 0.05 )
price_df . plot ( figsize = ( 18 , 8 ), title = '各类趋势线比较' )
从这个个例上看,LLT确实跟得更紧(接近MA5),同时做到了比较平滑(比EMA更平滑,接近MA30)。
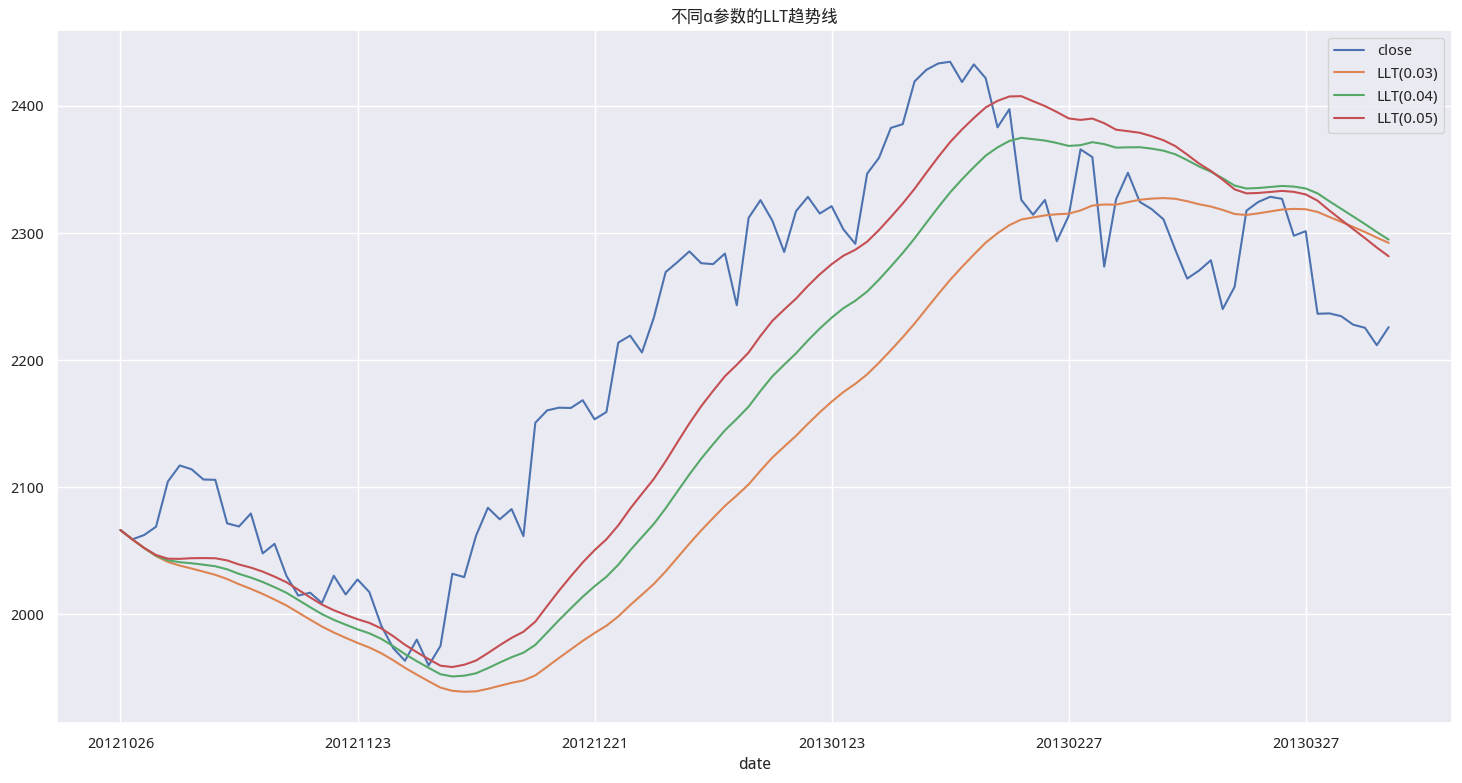
在计算LLT时,有一个\(\alpha\) 参数,它的取值对平滑程度和延迟性都有影响:
for a in [ 0.03 , 0.04 , 0.05 ]:
price_df [ f 'LLT(%s)' % a ] = calculate_llt ( price_df [ 'close' ], a )
show_cols = [ "LLT(0.03)" , "LLT(0.04)" , "LLT(0.05)" ]
price_df [ show_cols ] . plot ( figsize = ( 18 , 9 ), title = '不同α参数的LLT趋势线' )
回测与对比
我们先来看看传统均线的回测情况。我们将定义一个交易函数,它接受一个dataframe,因子列名和计算slope的窗口。后面我们在对LLT进行回测时,我们将使用同一个函数,这样可以确保对比的公正性。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61 import quantstats as qs
mport quantstats as qs
def trading_strategy ( df , factor_col : str , slope_window = 5 , long_weight = 0.5 , short_weight = 0.5 ):
"""
计算基于均线斜率的多空组合策略收益
参数:
price_df: 包含收盘价的DataFrame
factor_col: 因子列
slope_window: 计算斜率的窗口大小
long_weight: 多头仓位权重 (0-1)
short_weight: 空头仓位权重 (0-1)
返回:
DataFrame: 包含策略收益的DataFrame
"""
df = df . copy ()
df [ 'slope' ] = ( df [ factor_col ] . rolling ( slope_window )
. apply ( lambda x : np . polyfit ( np . arange ( slope_window ), x , 1 )[ 0 ]))
df [ 'signal' ] = 0
df . loc [ df [ 'slope' ] > 0 , 'signal' ] = 1
df . loc [ df [ 'slope' ] < 0 , 'signal' ] = - 1
# 计算每日收益率
df [ 'benchmark' ] = df [ 'close' ] . pct_change ()
# 计算多空组合收益
df [ 'long_return' ] = np . where ( df [ 'signal' ] == 1 , df [ 'benchmark' ], 0 )
df [ 'short_return' ] = np . where ( df [ 'signal' ] == - 1 , - df [ 'benchmark' ], 0 )
# 组合收益 = 多头收益 * 多头权重 + 空头收益 * 空头权重
df [ 'strategy' ] = df [ 'long_return' ] * long_weight + df [ 'short_return' ] * short_weight
return df
def backtest_ma ( start , end , win : int = 30 ):
price_df = get_price ( "000001.SH" , start , end )
factor_col = f "ma { win } "
price_df [ factor_col ] = price_df [ "close" ] . rolling ( win ) . mean ()
strategy_df = trading_strategy ( price_df , factor_col )
strategy_df . index = pd . to_datetime ( strategy_df . index )
qs . plots . returns (
returns = strategy_df [ "strategy" ],
benchmark = strategy_df [ "benchmark" ]
)
metrics = qs . reports . metrics (
returns = strategy_df [ "strategy" ],
benchmark = strategy_df [ "benchmark" ],
display = False
)
print ( metrics [: 10 ])
start = datetime . date ( 2005 , 9 , 6 )
end = datetime . date ( 2013 , 6 , 28 )
backtest_ma ( start , end )
我们在30日均线上,回测得到的结果,与研报基本一致,都在300%左右。
Tip
理论上,知道回测时间,我们应该能做到像素级的复现。但是,这里有一个重要的参数,即求斜率时的窗口大小,研报没有披露。我们在复现时,使用的窗口为5。
所以,在对LLT进行回测时,我们只需要先计算出LLT,再将LLT作为因子传入 trading_strategy 函数即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 def backtest_llt ( start , end , win : int = 30 , d = 20 ):
price_df = get_price ( "000001.SH" , start , end )
alpha = 2 / ( d + 1 )
price_df [ "llt" ] = calculate_llt ( price_df [ "close" ], alpha )
strategy_df = trading_strategy ( price_df , "llt" )
strategy_df . index = pd . to_datetime ( strategy_df . index )
qs . plots . returns (
returns = strategy_df [ "strategy" ],
benchmark = strategy_df [ "benchmark" ]
)
metrics = qs . reports . metrics (
returns = strategy_df [ "strategy" ],
benchmark = strategy_df [ "benchmark" ],
display = False
)
print ( metrics [: 10 ])
start = datetime . date ( 2005 , 1 , 1 )
end = datetime . date ( 2012 , 10 , 1 )
backtest_llt ( start , end )
运行结果表明,改用LLT均线之后,在同样的时间段,累积收益高出100%,夏普也由1.35提升到1.61,超额非常明显。
以上是研报复现的情况。研报发表时间较早,因此只回测到2013年,在此之后,情况如何?这个策略是否仍然有效?
如果把回测时间改到2013年之后,2024年底之前,保持alpha仍为0.05, 我们发现收益率对benchmark,仍有明显的超额。考虑到2015年之后,A股就一直没有大的行情,作为趋势跟随策略,收益不可能象之前那么好,也是理所当然。
不过,考虑增加alpha值(对应ema线窗口缩短)为0.1,以捕捉更短的波段,增加交易机会之后,则仍可以得到非常漂亮的超额和夏普:
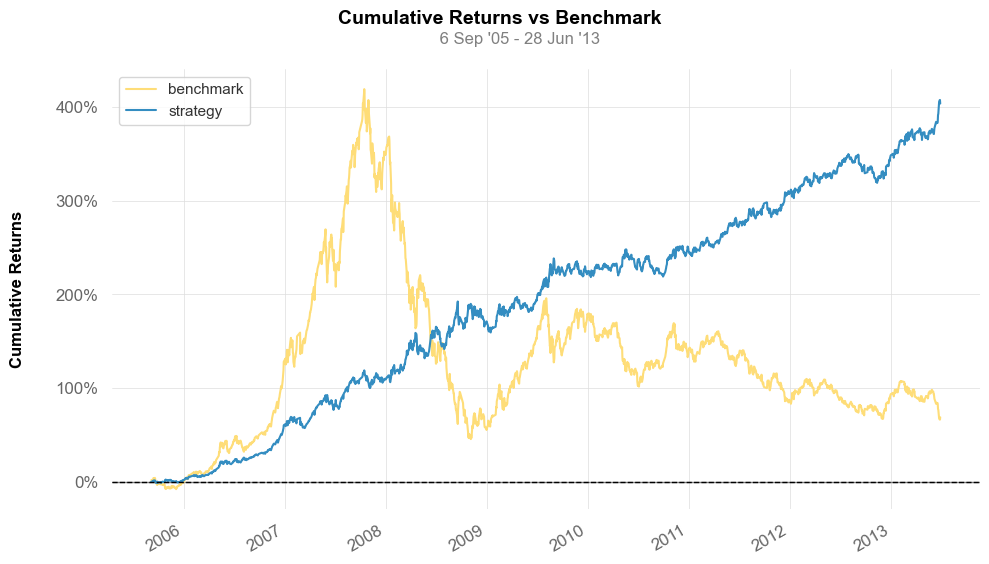
start = datetime . date ( 2013 , 1 , 1 )
end = datetime . date ( 2024 , 12 , 31 )
backtest_llt ( start , end , d = 10 )
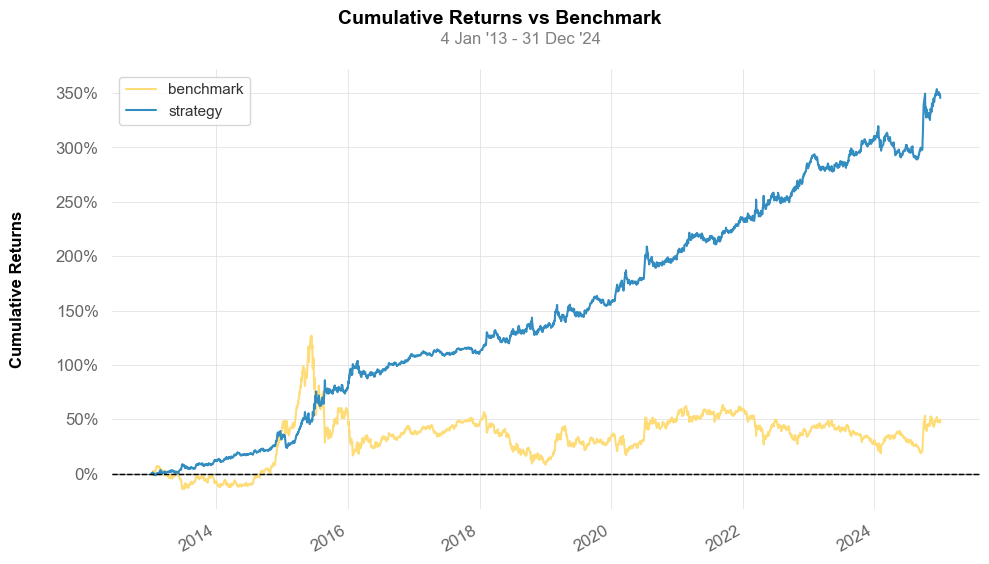
如果进一步增加alpha值到0.17(对应d=5)左右,则从2014年之后,上证指数多空组合收益达到了345%,夏普达到了1.33!
本策略全部代码以notebook格式发布在Quantide Research平台。加入平台后,可自行运行和验证此策略。