factor&strategy »
涨到溢出!PEPE告诉我,大盘还能涨几多?
这两天涨得喜气洋洋的,不过,对东财的程序小哥哥来说,可能还得加班了,因为涨得太好,程序溢出了:
这是什么情况?
温故而知新
在2024年9月,我们曾发表《节前迎来揪心一幕!谁来告诉我,A股现在有没有低估?》 一文。在那篇文章中,我们使用了akshare获取了上证指数的市盈率数据,并通过分位数和趋势分析,探讨了当时A股市场的估值情况。
当时我们的结论是:
如果仅从分位数统计来看,当下的A股是低估的。但如果考虑到市盈率总体上一直处在上升的趋势,以及最近一年来PE与指数涨跌的背离情况,判断A股是否已经低估还存有疑问,应该纳入更多维度进行判断。
现在是2025年8月,差不多快一年了。从成交量来看,市场似乎进入了狂飙期。我们去年使用过的技巧,是否还能用来预测未来的走势呢?
还是让数据说话。
使用 Tushare 获取指数市盈率
Tushare上周给我们放了一个假。不过,还好现在已经恢复了。要获取指数的市盈率,我们需要用到函数index_dailybasic。
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from datetime import datetime
pro = pro_api ()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 def get_index_pe_close ( ts_code = '000001.SH' , start_date = '20100101' , end_date = '20250825' ):
# 获取指数PE数据
df_pe = pro . index_dailybasic ( ts_code = ts_code ,
start_date = start_date ,
end_date = end_date ,
fields = 'trade_date,pe_ttm' )
df_pe . rename ( columns = { 'trade_date' : 'date' , 'pe_ttm' : 'pe' }, inplace = True )
df_pe [ 'date' ] = pd . to_datetime ( df_pe [ 'date' ])
df_pe . set_index ( 'date' , inplace = True )
# 获取指数收盘价数据
df_price = pro . index_daily ( ts_code = ts_code ,
start_date = start_date ,
end_date = end_date ,
fields = 'trade_date,close' )
df_price . rename ( columns = { 'trade_date' : 'date' }, inplace = True )
df_price [ 'date' ] = pd . to_datetime ( df_price [ 'date' ])
df_price . set_index ( 'date' , inplace = True )
# 合并数据
df = df_pe . merge ( df_price , left_index = True , right_index = True , how = 'inner' )
# 排序
df . sort_index ( inplace = True )
# 移除PE为空的记录
df = df . dropna ( subset = [ 'pe' ])
return df
得到 pe 数据之后,让我们先来看一下直观走势:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 # 绘制PE走势图
fig , ax = plt . subplots ( figsize = ( 12 , 6 ))
color = "tab:red"
ax . plot ( df . index , df [ "pe" ], label = "PE" , color = color )
ax . set_xlabel ( "Year" )
ax . set_ylabel ( "PE" , color = color )
ax . xaxis . set_major_locator ( mdates . YearLocator ())
ax . xaxis . set_major_formatter ( mdates . DateFormatter ( '%Y' ))
df = get_index_pe_close ( start_date = "20100101" )
# 添加分位数线
for i in range ( 1 , 4 ):
quantile = df [ "pe" ] . quantile ( i / 4 )
ax . axhline ( quantile , color = 'gray' , linestyle = '--' , label = f " { i / 4 : 02.0% } " )
plt . title ( "SSE Index PE Ratio (via Tushare)" )
plt . legend ( loc = "upper left" )
plt . grid ( True )
plt . show ()
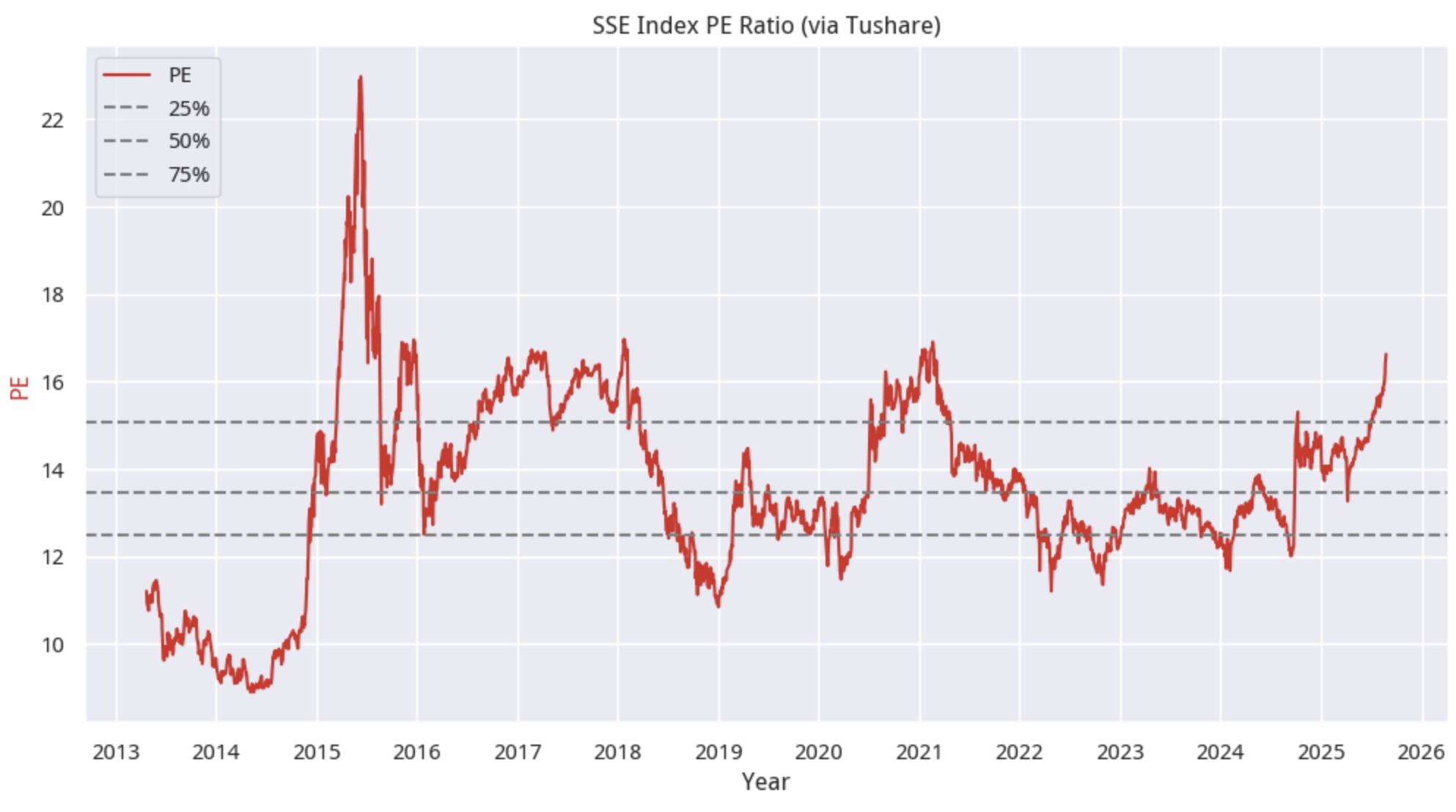
数据表明,如果我们忽略2015年那段癫狂的历史(场外融资加杠杆),那么现在的 PE 水平已经是相当高了。
到底有多高呢?
def show_pe_quantile ( df ):
# 计算当前PE分位数
current_pe = df [ 'pe' ] . iloc [ - 1 ]
rank = df [ 'pe' ] . rank () . iloc [ - 1 ]
percentile = rank / len ( df )
print ( f "当前PE分位: { percentile : .2% } " )
show_pe_quantile ( df )
df = df [ df . index > '2016-01-01' ]
show_pe_quantile ( df )
如果从2013年起(tushare 似乎没有更早的数据了)开始算,那么当前PE分位数为95.18% ;如果从2016年1月起算,那么当前 PE 分位数则已达到98.81% ,很快就要满分了。作为指数来讲,确实是有点高了。
当前的 PE 值,是多少天以来的最高值呢?通过 pandas 可以很容易计算出来:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 def find_days_since_max_pe ( df ):
"""计算当前的PE是过去多少天以来的最大值"""
if df . empty or len ( df ) < 2 :
return None
# 获取当前PE值
current_pe = df [ 'pe' ] . iloc [ - 1 ]
# 找到当前PE值在历史数据中的最大值位置
max_pe_idx = df [ 'pe' ] . idxmax ()
# 计算距离最大值日期的天数
current_date = df . index [ - 1 ]
days_since_max = ( current_date - max_pe_idx ) . days
return days_since_max , max_pe_idx
find_days_since_max_pe ( df )
答案是,现在的 PE 值是2018年1月24日以来的最大值,也就是创了7年来的新高。
假设指数能稳住,那么能让 PE 回到安全区的惟一答案,就是要靠企业利润增长了。如果指数就停在这个位置,要让 PE 回到安全区,需要企业利润增加多少呢?
我们通过下面的方法来计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 def required_earnings_growth ( df , target_percentile = 0.75 , target_index = None ):
"""计算使PE分位数降到目标值所需的盈利增长百分比"""
if df . empty :
return None
# 获取当前PE值和当前指数点位
current_pe = df [ 'pe' ] . iloc [ - 1 ]
current_index = df [ 'close' ] . iloc [ - 1 ]
# 如果指定了目标指数点位,则计算在该点位下的目标PE值;否则使用数据框中目标分位数对应的PE值
if target_index is not None :
# 根据PE = Price / Earnings,计算目标指数点位下的PE值
# 假设盈利不变,目标PE = target_index / (current_index / current_pe)
# 即 target_pe = target_index * current_pe / current_index
current_pe = target_index * current_pe / current_index
# 计算目标PE值(目标分位数对应的PE)
target_pe = df [ 'pe' ] . quantile ( target_percentile )
# 如果当前PE已经低于目标PE,则不需要盈利增长
if current_pe <= target_pe :
return 0.0
# 计算所需盈利增长百分比
# PE = Price / Earnings => Earnings = Price / PE
# 要使PE从current_pe降到target_pe,需要:
# (Price / target_pe) / (Price / current_pe) - 1 = current_pe / target_pe - 1
required_growth = ( current_pe / target_pe ) - 1
return required_growth
required_earnings_growth ( df )
通过计算可知,在现有的指数上,如果要让 PE 回到75%分位以下,那么企业利润需要增加10.2%。如果要让 PE 回到84.13%分位(即一个标准差)以下,那么企业盈利需要增长5.5%。根据企业的年利润增长水平,我们大致可以估算出这需要多少年。当然,这要求企业的年利润增长水平必须是正的。
如果我们希望指数能上涨到4000点,PE 还要回到一个标准差以下,那么企业利润必须增长8.68%以上。
情况就是这么个情况。总之,我们已经进入了『无人区』,没有数据可以利用了。
本文代码可以匡醍研究平台运行和下载。