PDF is all you need(2)
Table of Content
在上一篇中,我们使用了初等概率的方法来解题。这种方法,需要我们『数』出来样本空间总数和各个事件包含的基本事件数。两者的商即为概率。
如果基本事件不可数,我们还可以使用几何概型,将计数转化为『长度、面积或体积』的比值计算。
但是,这些方法既需要较高的技巧,也往往要求事件有限、基本事件在几何区域服从均匀分布等等条件。这就像很多小学奥数题,题目本身不难解,但是限制我们只能使用初等数学的知识来解答之后,对『技巧』的要求就变高了:你得将在高维世界下,很简单的东西,依靠敏锐的数学直觉和复杂的技巧,映射成为低维世界下可理解、可求解的对象。而且,这个过程中我们对解题过程的描述,更多地使用了含混的自然语言而非精确的数学语言,这也会使得我们的答案的正确性显得可疑。
在上一篇中,我们已经感受到了这种窘迫。解题思路看上去很简单,但实际上为了找到正确答案,我已经换了好几个版本的解题思路。几乎每一个版本,都杂糅着很多定义不清晰的自然语言描述,特别是在为什么要去重复这件事情上,总感觉像是说清了,又感觉没有太说清,很有点凭直觉得到通项,再用前几项去解释公式的『凑答案』的味道。直到最后,我找到\(n\)个点同属一个半圆,就等价于\(n\)个点能张出的最大张角小于\(\pi\)这样一个等价描述,在去掉重复统计的事件这件事情上,我才算是找到了精确的数学语言。
Info
显然我并不是唯一一个发现古典概率中,使用自然语言描述会带来含混不清和歧义问题的人。1889年,数学家贝特朗就提出了这样一个悖论:在一个圆内任意画一条弦,求这条弦的长度大于圆内接正三角形边长的概率。基于三种合理、而不同的随机画弦的理解,这道题可以有1/2, 1/3和1/4三种不同的答案。
但我们为什么不去掌握更精确的数学语言以及更趁手的数学工具,从而简化我们思考的复杂性呢?
什么是概率¶
人类最早认识到概率问题,来源于赌博。比如,1654 年,法国贵族赌徒梅雷骑士向数学家帕斯卡提出了一个经典问题:两人赌博时约定先赢满 5 局者获胜,若中途中断,如何根据当前胜负情况(如一人赢 4 局、另一人赢 2 局)公平分配赌金?
这个问题的核心是计算 “剩余对局中双方获胜的概率”,帕斯卡与费马通过书信交流,首次系统地用组合数学计算了这种 “预期概率”,为概率论奠定了早期基础。
从赌博到古典概率¶
在赌博中,很多场景具有『有限个等可能结果』的特点,并且赌徒需要计算『有利结果』与『总结果』之间的比例。这种比例思想,就被数学家们提炼成为古典概率的定义。
其核心观点是,随机事件由若干『等可能性』的、相互独立(互斥)的基本事件组成,通过对组成『事件』的『基本事件』进行计数,就可以得到『事件』的概率。
比如,掷一枚均匀硬币,可能出现的结果为正面朝上(记为H)和反面朝上(记为T)共 2 个基本事件,这2个基本事件是等可能出现的,即各自发生的概率都是\(1/2\);并且,在一次实验中,一旦出现一个基本事件,就不再会出现其他基本事件。所以,上述2个结果就是2种『基本事件』。
在上述前提下,问:
Question
抛一枚均匀硬币3次,恰好出现2次正面的概率是多少?
题目要求的事件由基本事件构成,所有可能的基本事件组合是:
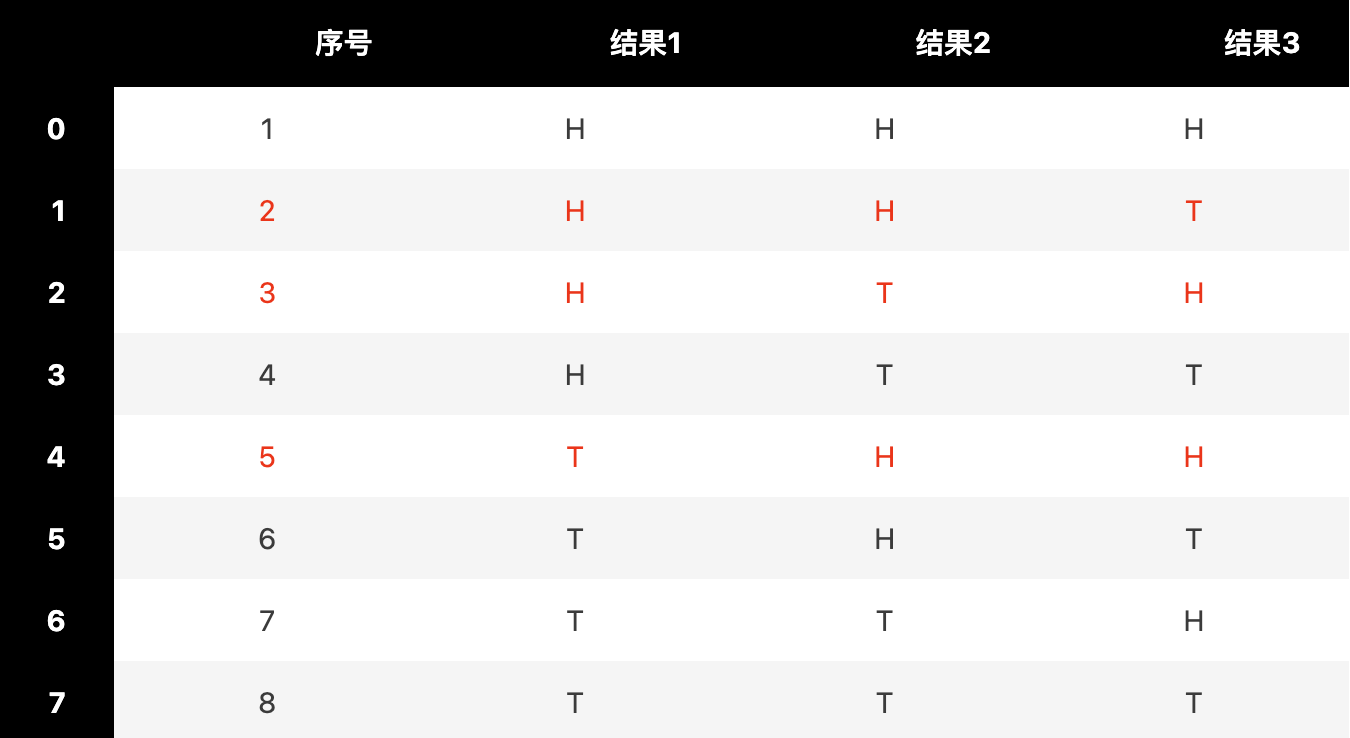
其中有且仅有两次正面朝上的事件共三次,分别为序号2,3,5。由此我们总结出来古典概率的公式:
在问题规模比较大时,上述列举法会遇到计算困难问题,这时我们可能套用一些经典公式。比如上述问题就可以套用二项分布的通用公式:
Tip
但是,我们发现,上述解题过程中,基本事件、事件这些概念不太好区分。比如,在掷骰子的例子中,如果要问只掷一次,那么出现数字1的概率是多少?这时候基本事件就与事件完全等同了。
此外,对基本事件的计数,有时候也容易与频率概念相混淆,比如,在掷骰子的例子中,随手丢三次骰子,有两次出现了1,那么计算1出现的概率时,为什么不是 2(即出现1的次数)除以3(即扔了 3 次)?原因是,基本事件组成事件,是一个思想实验,与实际投掷次数无关。
Info
概率与频率是比较容易混淆的概念。
如果事件发生的次数足够多,则我们可以用某事件(比如事件A)的统计次数(\(n_A\))除以事件发生总数(\(n\)),得到的事件A发生的频率\(f_n(A)\)来逼近事件A的概率\(P(A)\)。
这说明,古典概率理论就连在自己擅长的领域--离散概率时,都容易出现混淆不清、似是而非的问题,需要我们进一步拓展、公理化相关概念。
此外,古典概率还解决不了这样的问题:
Question
在 [0,1] 区间随机取一点,落在 [0.2,0.5] 的概率是多少?
古典概率要求基本事件是有限可数的,而上述问题中,基本事件是无穷的,因为在[0, 1]之点,存在着无穷多个点。
当基本事件无限但具有几何意义时,我们就可以用几何概率的思路来求解问题。
从有限到无限:几何概率的提出¶
几何概率的基本模型是:
- 所有可能的试验结果(样本空间)对应一个可度量的几何区域 \(\Omega\) (如线段、平面区域、空间立体等);
- 每个基本事件的发生对应区域 \(\Omega\) 内的一个点,且点在区域内均匀分布(即 “等可能” 表现为点在区域内任何位置的概率相等)。
此时我们可以用以下公式来表述概率:
Tip
基于上述定义,我们就可以求出问题2的答案为 \((0.5 - 0.2)/(1-0) = 0.3\)。
在这个定义中,长度、面积、体积都是“测度”的具体表现。在现代数学中,这个概念被严格化为“勒贝格测度”(Lebesgue Measure,1901年提出),它将我们对长度、面积和体积的直观理解推广到更复杂的集合上,为几何概率提供了坚实的理论基础,也为后面概率的公理化奠定了基础。
在勒贝格测度中,简单的区间 \([a,b]\) 对应的勒贝格测度就是 \(b-a\),和我们平时说的长度完全一样。对于单点,它的勒贝格测度是0,因为一个点没有 “长度”。
几何概率的核心前提是『均匀分布』,即样本空间内的点均匀分布,概率与区域度量成正比,并且还需要有办法度量区域。因此,还有不少概率问题是几何概率无法解决的,比如:
灯泡的寿命服从指数分布,如何计算寿命大于 1000 小时的概率? 此时就很难通过 『时间区间长度比』直接计算了。
但是,几何概率的出现,已经为现代概率论提供了基础,因为我们很容易把几何测度与积分联系起来。于是,1933年,数学家Andrey Kolmogorov(柯尔莫哥洛夫)就在总结古典概率、几何概率等早期模型的基础上,于 1933 年提出了概率的公理化定义,将概率从具体场景抽象为数学上的严格理论。
柯尔莫哥洛夫公理¶
设随机试验的样本空间为\(\Omega\),对每个事件A(即\(A \subseteq \Omega\)),赋予一个实数\(P(A)\),若\(P(A)\)满足以下三条公理,则称\(P(A)\)为事件A的概率:
- 公理 1(非负性):对任意事件A,\(P(A) \geq 0\);
- 公理 2(规范性):样本空间\(\Omega\)作为必然事件,其概率为 1,即\(P(\Omega) = 1\);
- 公理 3(可加性):若事件\(A_1, A_2, \dots\)两两互斥(即任意两个事件没有共同样本点),则\(P(A_1 \cup A_2 \cup \dots) = P(A_1) + P(A_2) + \dots\)。
Info
这个公理由Kolmogorov在1933年提取。Kolmogorov是俄国数学家,他与Smirnov共同提出了Kolmogorov-Smirnov test(即KS检验),该理论用来检验一个样本是否来自某一特定的理论分布,或者两个概率分布是否存在显著差异。
这个定义虽然很抽象,与我们初学概率时形成的直观印象有很大差别,甚至概率\(P(A)\)本身未必直接代表事件A发生的可能性大小。
但正是这种抽象的定义,使得连续随机变量与离散随机变量(离散事件)能够在同一框架下统一描述。两者的区别只体现在概率的计算方式上:离散情形下通过对各事件概率求和,连续情形下则需用积分来计算。实际上,积分可以看作是一种“连续求和”或“求面积”的过程,因此两类问题在本质上是统一的。
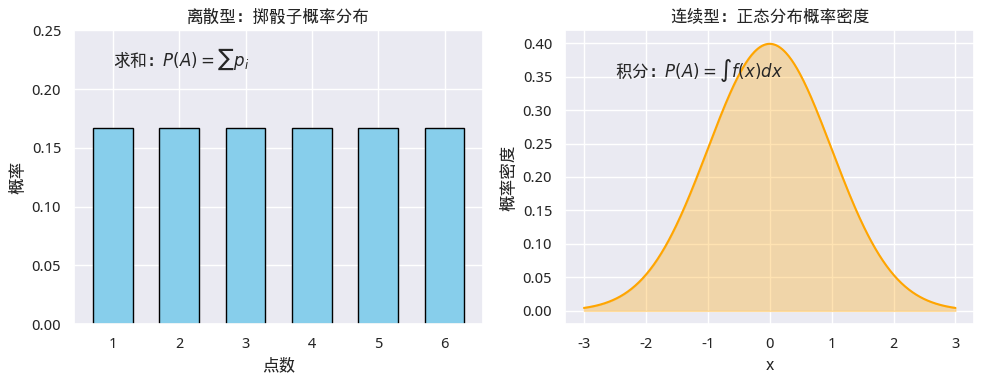
然而,随着实际问题的复杂化,单靠直观或简单计数方法已难以胜任。为此,我们需要更强大的数学工具,才能系统地刻画和计算概率。因此,通过公理化,概率的定义不再依赖具体场景或直觉假设,而是建立在清晰的数学基础之上,既能处理有限、离散问题,也能推广到无限、连续情形。在柯尔莫哥洛夫公理的基础上,我们就步入了现代,从牛顿时代起建立的数学工具——积分和导数,终于可以派上用场了。