量化面试神题:圆上随机点的概率陷阱
常常有人问,做量化交易需要什么样的数学基础?
不同领域的量化研究员需要数学基础是不一样的,一般是期权 > 高频 > 期货 > 股票中低频量化。
今天我们就聊聊各个领域要求的数学基础,并且以一道经典的量化面试题(来自绿皮书),介绍在概率知识上,从低级到中级,机构可能会考察哪些概念。
本文较长,将分两部分刊出。
股票中低频量化¶
我们需要掌握基础的概率论与数理统计。比如统计变量的分布特征(均值、方差、分位数);掌握什么是假设检验(如何判断显著性等);线性回归;相关性分析等。
统计变量的分布特征是基础中的基础,在量化中无时不刻被使用。比如,要评判两个量化策略谁更好?最基础的指标就是它的日均收益率。但是,如果你有基础的统计学知识,就很容易明白,均值相同,并不意味着两个随机变量具有同一性。因此,就很容易理解为什么要使用几何收益代替日均收益率来判断两个策略赚钱能力的指标了。扎实的统计学基础,可以帮助我们拓展概念,懂得什么场合下使用哪一个概念。这只是其中一例。
在多因子策略中,我们会广泛使用线性回归,来确定因子权重(因子权重对远期收益率的回归)。此外,在多因子策略中,我们需要通过正交化,以抵消关联因子的影响,常常也是通过线性回归求残差的方法,来获得正交化后的因子。
在判断因子有效性时,就会涉及到显著性检验相关理论,要理解什么是 p 值,什么是 t 值。
相关性分析也用在因子挖掘中。我们通过相关性检验(Pearson 或者 Spearman)来判断因子对远期收益的涨跌是否有相关性。
当然,我们还要掌握正态分布。了解它的分布特性,几个关键分位数(\(\mu + \sigma, \mu + 2\sigma, \mu + 3\sigma\))等,了解它产生的原理以及适用范围。
线性代数和微积分这一块,如果不接触机器学习,可以不必掌握太深入。在使用时,借用现成的 Python 库即可。但是建议深入掌握 PDF(概率密度函数)和 CDF(累积分布函数),掌握它们之后,理解初等概率问题,就会像掌握微积分之后,再来解小学奥数问题那么简单。
这些知识基本上都涵盖在《量化 24 课》中。
期货量化¶
这部分要求掌握时间序列分析,比如 GARCH 模型,协整检验等。比如,我们可能有一个螺纹钢期货跨期套利策略,要确认近月与远月合约价格存在长期均衡关系,然后才有套利的基础。这就要求深入理解时间平稳序列的意义,协整的概念以及如何进行协整检验等等。
高频量化¶
高频量化涉及到订单流建模、短期价格预测、最优下单策略等算法,对概率与数理统计的要求就更高一些。
比如,在订单流方向预测中,往往会用到条件概率、极值理论。对价格分布建模时,就要用到核密度估计(KDE 法)建模,通过假设检验来验证。在订单到达模型中,可能要使用泊松过程;在短期价格状态转移预测时,可能要使用马尔可夫链。这些都是随机过程中的内容,属于概率论中的高级阶段了。
此外,还常常涉及优化理论(凸优化),比如,高频做市商的最优报价策略,就是一个凸优化求解过程,也可能使用动态规划算法(最优下单时点选择)。
当然,也存在另外一条路径,就是深入掌握机器学习理论与实践框架之后,力大飞砖,这种情况下,对上述数学的要求可能可以降低。
由于高频量化对速度要求很高,因此很多运算要求通过矩阵运算来提高效率。所以,也会对线性代数有一些要求。
期权量化¶
期权量化中的核心问题是衍生品定价、波动率建模、风险对冲(Greeks 计算)。这部分对数学的要求最高,一般要掌握布朗运动、伊藤引理、随机微分方程、偏微分方程、高阶导数(用于 Greeks 的计算)、复分析等。
总之,期权是一种被『设计』出来的衍生品,对数学深度和推导能力要求极高,是量化领域中,对数学能力要求最高的一个。
那么,在机构招人时,对概率、统计题一般会考察到什么深度?我们下面拿一道机构面试题作为例子,说明在不涉及期权交易的情况下,我们需要对概率统计掌握到什么程度。
我们会讲得细一点,题目的解法会分两部分,分步涵盖初等概率解法和积分、PDF 等工具解法。
多点共半圆问题¶
这是绿皮书上的一道题:一个圆里随机取 n 个点,它们在同一个半圆的概率是多少?
Tip
不要把这个问题与经典的多点共圆问题混淆。多点共圆是指在同一个平面上的 n 个点,是否存在一个共同的圆,使得这 n 个点都落在该圆的圆周上。
这道题可以用初等概率知识来解答,也可以使用积分、PDF 等工具来解答。这里我们两种解法都提供,特别是通过后一种,把相关的概念都串联起来。
初等概率法¶
初等概率侧重直观理解和基本计算,不涉及过于复杂的数学工具。但如果构思巧妙,也可以解决比较复杂的概率问题。本题即是一例。
我们首先引入下图:
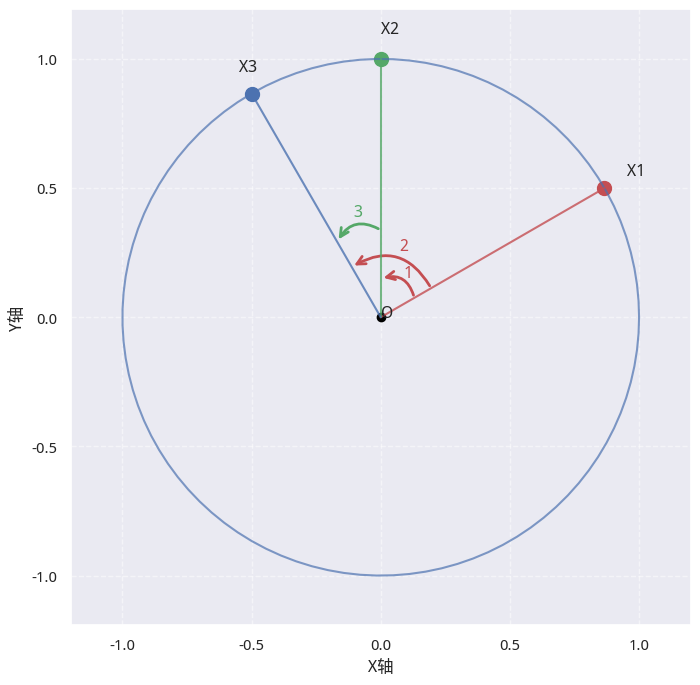
在图中,每个点(比如 A,B,C),都与水平蓝实线 OE 构成一个夹角,计为\(\theta_A\), \(\theta_B\), \(\theta_C\)等,即:
依次类推。从每个点起,都存在一个顺时针的圆弧\([\theta_x, \theta_{max}]\),当该圆弧长度小于等于半圆时,就满足题目要求。在图示中,我们可以用\(\angle AOC\)来表示这个圆弧--它也是\(n\)个点所能张出的最大角度(特指小于 180 度的角度)。
根据题意,\(\angle AOC\)与\(\angle COA\)本质上是同一个圆弧。这一点在后面要用到。
现在,我们就正式开始讨论。
第一步,假设我们从 n 个点中,随机抽取一个点进行固定(记该点为 A),以此为基础,计算后面发生符合题目要求情况的概率,记为\(P_A\)。
第二步,我们再从余下的\(n-1\)个点中,随机抽取一个点 B。此时 B 可能落在 A 的两边(注意两事件互斥,概率之和为 1),但都满足题目要求。因此,当\(n=2\)时,\(P_A\)的概率为 \(\frac{1}{2}+ \frac{1}{2} == 1\)。
这里要注意,总概率\(P\)是\(P_A\)与\(P_B\)之和,于是,此时会有:
概率居然会大于1!这是怎么回事呢?在列举事件发生的各种情况时,我们一定要注意事件要满足互斥条件(也就是不能重复统计)。在我们上述推导过程中,其实是存在一个重复统计情况的。因为此时\(\angle AOB\)与弧\(\angle BOA\)实际上是同一个圆弧,只能算一个事件,但我们却统计了两次(分别固定 A 和固定 B),这样就产生了重复统计。
所以,此时的概率应该是:
第三步,我们再从余下的\(n-2\)个点中,随机抽取一个点 C。此时 C 可能落在\(\overrightarrow{AB}\)方向上,也可能落在\(\overrightarrow{BA}\)方向上。由于 B 和 C 落在何处,是独立同分布(都是均匀分布)事件,所以,此时\(P_A\)的概率是
我们还要继续讨论重复统计的情况。假设点 A、B、C 满足题目条件,且\(\theta_C\)最大,则三点属于同一个最大张角\(\angle AOC = \angle COA\) 。
从图中可以看出,在讨论\(P_A\)时,ABC 同在张角\(\angle AOC < \theta_A + \pi\)上,满足题目要求,被统计一次。在讨论\(P_C\)时,ABC 同在张角\(\angle COA < \theta_C - \pi\)上,仍然满足条件,此时又被统计一次。但本质上,张角\(\angle AOC\)与\(\angle COA\)是同一个角,同一个事件,但被统计了两次。
Tip
在讨论\(P_B\)时,在由点 B 出发,能张出的任意一个角都不会是\(\angle AOC\)或者\(\angle COA\)中的一个,因此它们不会被统计。
从以上讨论,我们可以得出以下规律,如果由n个点能张出的最大角\(\alpha\)满足小于\(\pi\)的要求,则该最事件会分别在计算\(\theta_{min}\)和\(\theta_{max}\)对应的点的概率时,被重复统计一次。
因此,对于任意 \(n\) 个点\(X_1, X_2, ..., X_n\),我们得到该\(n\)点可以落入同一个半圆的概率应该由以下公式计算:
而在有\(n\)个点时, \(P_{X_i}\)的取值由上述讨论可知,为\(\frac{1}{2^{n-2}}\)。故,\(n\)能落在同一个半圆的概率为
在初等概率的范畴内,我们需要理解一些初级分布(比如均匀分布、伯努利分布)、独立事件等等原理,并巧用几何概率的思想来进行解题。
在下一篇,我们将全面还原概率、概率密度函数、分布函数、期望等关键概念,以及数学概念是如何由具体到抽象的。