投资组合理论与实战(2) - 蒙特卡洛方法

---

Table of Content

所谓蒙特卡洛模拟，就是随机产生大量的资产分配方案，然后再计算各种分配方案下，所得到的波动率、夏普率，再根据最优的夏普率，反查资产分配方案。

主要操作我们在上一节已经介绍过，这一步主要做的事情是不断地重复。我们先把代码给出来，再进行解释：

num_ports = 5000

w = np.zeros((num_ports, len(stocks)))
vol_arr = np.zeros(num_ports)
sharpe_arr = np.zeros(num_ports)
port_return_arr = np.zeros((num_ports, len(returns)))
cov_arr = np.zeros(num_ports)

for i in range(num_ports):
    weights = np.array(np.random.random(len(stocks)))
    weights = weights/np.sum(weights)  

    w[i,:] = weights

    weighted_returns = weights * returns
    port_return_i = weighted_returns.sum(axis=1)
    port_return_arr[i,:] = port_return_i

    cov = np.cov(port_return_i)
    cov_arr[i] = cov
    vol_arr[i] = np.sqrt(np.dot(weights.T, np.dot(cov, weights)))
    sharpe_arr[i] = sharpe_ratio(port_return_i)

我们主要定义了这样四个数组：

1. 权重矩阵 all_weights。我们打算重复 5000 次采样，由于资产组合共有 4 个标的，所以，它是一个 5000 * 4 的矩阵。每一行对应一次资产组合分配。
2. 夏普率数组。它是一个 size 为 5000 的数组，记录了每一次计算出来的 sharepe 率。
3. 波动率数组。它也是一个 size 为 5000 的数组，记录了每一次计算邮来的波动率。
4. port_return_arr，在示例中，它是一个 5000 * 241 大小的矩阵，每一行记录了组合在过去一年中每一天的收益。

当上述代码运行完成之后，我们就得到了 5000 组夏普值。根据夏普值的定义，我们直接找到夏普值最大的那一组，就是风险最小、收益最高的资产组合。

确定最佳投资组合

我们使用 np.argmax 来寻找夏普最大时的位置，此点即为最佳投资组合：

# 检查最高的 SHARPE
pos = np.argmax(sharpe_arr)
print(pos, sharpe_arr[pos])
print("stocks", stocks)
print("Portfolio Allocation:", w[pos])

这样我们得到资产分配方案类似如下：

	标的 1	标的 2	标的 3	标的 4
比例	35.3%	0.3%	0.8%	64%

我们将上述试验结果绘制成图形，来看看是否符合有效前沿理论：

import matplotlib.pyplot as plt

annual_return = np.prod((1 + port_return_arr), axis=1) - 1
plt.scatter(vol_arr, annual_return, c=sharpe_arr, cmap='RdYlBu')
plt.colorbar(label='Sharpe Ratio')

plt.scatter(vol_arr[pos], annual_return[pos], c='red',s=80)

我们以波动率为 x 轴，年化回报为 y 轴。在每一个 x 上，都存在若干组年化回报数据，有正有负。显然，对于同一个 x，正好是那些处在有效前沿上的组合，正好是收益最大或者亏损最大的组合。

按照 MPT 理论，只有那些在 y 轴上方，且处于有效前沿上的才是值得关注的组合，然后根据我们的风险承受能力，来选择这条线上对应的组合。

我们把夏普率最高的那组方案，用红色的点标注出来。

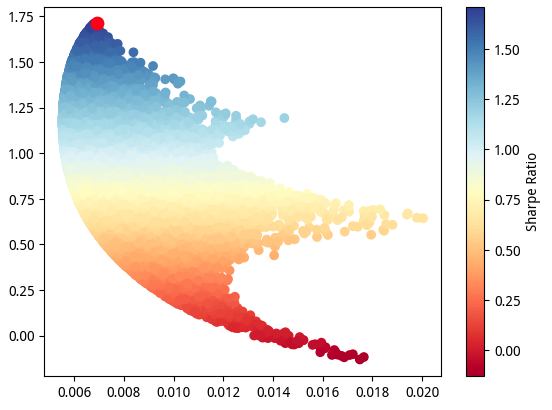
从走势图来看，我们这样求出来的资产组合确实是最优的。但是，如果我们将它与文章开头的那个图相比，我们会得出什么结论？

1. 这把牌不行。如果你愿意承担较大风险，这把牌也不能给你想要的收益。浪得不够狠。

2. 资产组合并没有形成直观的有效前沿，原因主要是投资组合整体的收益率受组合内资产的收益率限制，即min(组合内资产收益率)≤资产组合收益率≤max(组合内资产收益率)，因此并不是能实现所有收益率。

因此我们得到结论：你得重新选标的。

另外，如果你现在就急于用MPT来进行投资。。。你还得再学点啥。

历史当然总是在重复自己，一切历史都是当代史。但是仍然有很多东西要讨论。

首先，我们应该放多少支标的到这个组合里来？我们的示例中只使用了4支，如果我们对沪深300或者中证1000来做指增，会不会更好一点？

其次，上述两幅图是针对同一资产组合，不同时间段情况所形成，很明显收益及风险都有较大差异。如果我们在不同的时间点来优化投资组合，我们得到的仓位显然会有所不同。因此我们提出问题：我们应该多久计算一次并执行调仓？会不会有这样一种情况，每次调仓是在用过去的最优解，而它很快就变成了次优或者最劣解？也就是，这个组合它的动量周期是多久？

显然，任何一个有价值的方案，往往都不是一篇短文能cover的，我们会在后续的文章中不断深入探讨这个问题。

好，我们先放下这些问题，先来看一个技术问题：

执行上述循环5000次，我们花了大约 5.2 秒。

这是只有4支标的的情况。很显然，随着标的数的增加，我们需要暴力搜索的空间也随之变大。这种方法，在标的数增加到50支、100支时，是否还可行呢？

在讨论可行性问题前，我们可以尝试进行一些速度优化。

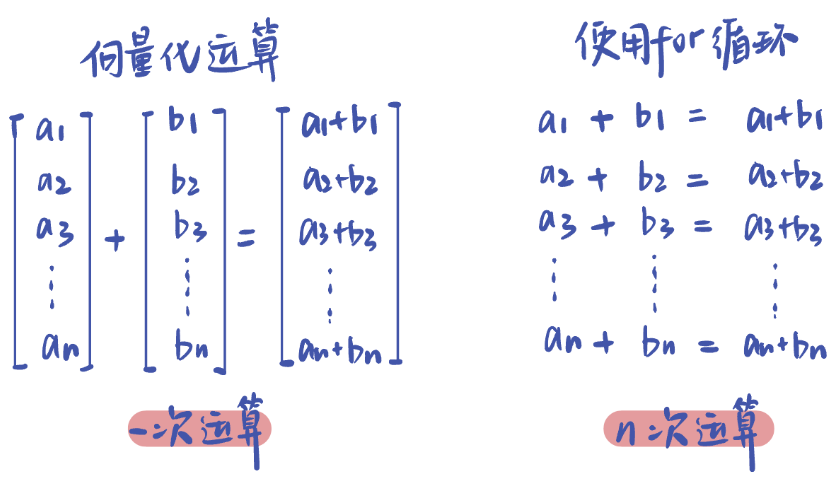
我们可以使用下面的算法，把部分计算移出了循环：

from empyrical import sharpe_ratio
import time
start = time.time()
num_ports = 5000
all_weights = np.random.rand(num_ports, len(stocks))

shape = (len(all_weights), -1)
all_weights = all_weights/all_weights.sum(axis=1).reshape(shape)

# got 241 daily summed returns over 5000 iters
all_port_returns = np.dot(all_weights,returns.T)

all_cov = np.cov(all_port_returns).diagonal()

# 计算波动率
all_vol = []
all_sharpe = []

annual_return = np.prod((1 + all_port_returns), axis=1) - 1

for i in range(num_ports):
    all_vol.append(np.sqrt(np.dot(all_weights[i].T, np.dot(all_cov[i], all_weights[i]))))
    all_sharpe.append(sharpe_ratio(all_port_returns[i]))

end = time.time()
print("计算用时", end-start)

# 绘图
all_vol = np.array(all_vol)
pos = np.argsort(all_vol)

plt.scatter(all_vol, annual_return, c=all_sharpe, cmap='RdYlBu')
plt.colorbar(label='Sharpe Ratio')

max_sharpe_pos = np.argmax(all_sharpe)
plt.scatter(all_vol[max_sharpe_pos], annual_return[max_sharpe_pos], c='red',s=80)

不过，在按行计算波动率和夏普率的时候，我不得不做出妥协，改用循环。在这种情况下（投资组合中只有4只标的），我们现在的执行时间需要0.65秒。提升了大概8倍的速度（初始为5.2s左右）。

PyPortfolioOpt的作者曾在一个示例中用到了这样的方法：

n_samples = 10000
w = np.random.dirichlet(np.ones(ef.n_assets), n_samples)
rets = w.dot(ef.expected_returns)
stds = np.sqrt(np.diag(w @ ef.cov_matrix @ w.T))
sharpes = rets / stds

计算速度非常之快（小于0.1秒），但需要对其中的ef.cov_matrix进行替换，感兴趣的同学可以研究下它的源码。

对于一个仅有4支标的的组合来说，这个速度（不到1秒）显然可以令人满意了。但我们也在上一篇文章中，提出一个问题，随着标的数的增加，使用蒙特卡洛模拟方法，我们需要暴力搜索的空间也随之变大。那么，究竟会增大多少呢，此时还可不可行？

我们先来看只有两支标的情况。假设资产权重的间隔是1%，即某个资产要么分配1%，要么分配2%，而不会分配1.05%这样的非整数权重。这样我们就可以算得，如果要把这些权重分布全部模拟到，搜索空间将是：

A: 1-100 ~ 101个选择项 B: 1个选择项

当A的权重选定以后，在权重和为1的约束下，B就只有一个选择。因此，总共是101次搜索。

当如果标的数量上升，我们为了模拟尽可能多的情况，一定会扩大模拟次数，因此总的运行时长迅速上涨。同时随着标的数的增加，我们要搜索的次数需要呈指数级增加，而不是按标的数线性增加。

因此，搜索次数是一个组合问题。假设存在四个标的，并不是简单的4×100就可以模拟出所有组合，而是存在： \(C_{99}^3\)种分配方案。

对任意n个标的，每个标的的权重间隔按1%计算的话，这个搜索空间将是：

\(C_{101-(n-1)}^{n-1}\)次。如果我们有50支标的，则需要搜索最少1.998e+21亿次！

Tip

可以使用 math.comb来计算组合数。

所以，使用蒙特卡洛方法，会存在无法穷尽所有样本空间的可能性。我们必须采用数学的方法，来优化这个求解过程。