资本资产定价模型

Table of Content

资本资产定价模型（CAPM）描述了资产的预期回报与市场系统风险之间的关系。它由威廉. 夏普等人在 1960 年代提出。威廉. 夏普获得了 1990 年的诺贝尔经济学奖。CAPM 被认为是经济学的七个基本理论之一。

CAPM 表示资产的预期收益等于无风险收益加上风险溢价。 CAPM 的假设是投资者是理性的，希望获得最大化回报并尽可能降低风险。因此，CAPM 的目标是计算相对于无风险利率的给定风险溢价，投资者可以预期获得的回报。

基本概念¶

Risk-Free Rate（无风险利率）¶

当投资者决定买入股票等高风险资产时，他的目的是为了获得高于无风险资产的收益。一般认为，银行存款利率和国债收益率都是无风险的。不过，一般同期的国债收益率会高于同期银行存款，所以我们常把国债收益率当成无风险利率。不同期限的国债利率收益不同，一般对标时，使用与风险资产预期投资时间相同就好。比如，如果是流动性好的股票，也不打算长期持有，则我们可以使用一年期国债利率作为无风险利率。如果是不动产，则可以使用 5 年期国债利率作为对标的无风险利率。

如何获取国债利率呢，我们可以通过 akshare:

import akshare as ak
import arrow
import numpy as np
import random
import pandas as pd

random.seed(78)

now = arrow.now()
start = now.shift(years=-1)
end = f"{now.year}{now.month:02d}{now.day:02d}"
start = f"{start.year}{start.month:02d}{start.day:02d}"

bond = ak.bond_china_yield(start_date=start, end_date=end)
bond.set_index(keys='曲线名称', inplace=True)
bond

这样我们就得到了近一年的各种债券收益率。我们可以把“中债国债收益率曲线”一年期的平均值当作一年期国债收益：

rf = bond[bond.index=='中债国债收益率曲线']['1年'].mean()
print(rf)

rf = rf / 100

输出是 2.06。这个值应该解读为 2.06%。

市场回报 \(r_m\)¶

市场回报率表示为\(r_m\) ，包括市场上的所有证券。但一般我们只使用某些指数，比如上证 50，沪深 300。如果投资偏好成长股，则可以使用中证 1000。

𝛽 贝塔¶

𝛽 是衡量股票相对于整体市场（例如沪深 300 指数）波动性的指标。换句话说，𝛽 代表回归线的斜率，即市场回报与个股回报的关系。

CAPM 中使用 𝛽 来描述系统风险或市场风险与资产预期回报之间的关系。根据定义，我们说整个市场的贝塔值为 1.0，个股根据其相对于市场的波动程度进行排名。

如果个股的 Beta = 1.0，这意味着其价格与市场完全相关
如果 Beta < 1.0（称为“防御性”），这表明该证券理论上的波动性低于市场
如果 Beta > 1.0 或“激进”，则表明资产价格比市场波动更大

CAPM 公式¶

该公式定义如下：

\[ r_i = r_f + \beta(r_m - r_f) \]

这里： * \(r_i\)是证券（个股）的预期回报 * \(r_f\)是无风险利率 * \(\beta_i\)是证券相对于市场的𝛽值 * \(r_m - r_f\)被称为风险溢价

我们通过一个例子来解读这个公式。如果标普 500 的整体回报率是 12.4%，无风险率利率为 0%，而 APPL 的𝛽为 1.1 的话，则投资者买入 APPL，他期望获得 13.7%的回报，以补偿承担的额外风险。

要使用 CAPM 模型，核心是计算个股相对于市场组合（指数）的𝛽。下面我们就通过 Python 来进行实现。

基于 Python 的 CAPM 实现¶

我们使用的市场组合是沪深 300，因此，我们也要从中抽取个股。我们将随机抽取 10 支个股来进行计算。

获取数据¶

为了确保所有人都能拿到数据，我们仍然使用 akshare。

首先，我们通过 akshare 获取过去一年的沪深 300 的行情数据：

import akshare as ak

hs300 = ak.stock_zh_index_daily(symbol="sz399300")
hs300.index = pd.to_datetime(hs300["date"])
print(hs300)

我们对过去一年的沪深 300 的收益情况进行速览：

now = arrow.now()
year_ago = now.shift(years = -1)

year_ago = hs300[hs300.index >= np.datetime64(year_ago)].index[0]
# PRINT(YEAR_AGO)

# 计算买入并持有的收益（最近一年）
buy_price = hs300[hs300.index == year_ago].iloc[0]["close"]
buy_and_hold = hs300["close"][-1]/buy_price - 1
print(f"买入并持收益：{buy_and_hold:.2%}")

# 通过均值推算年化收益
market_returns = hs300["close"].pct_change().dropna()
market_annual = (1 + market_returns[market_returns.index >= year_ago].mean()) ** 242 - 1
print(f"年化收益：{market_annual:.2%}")

可以看出，过去一年里，以买入并持有法计，沪深300的收益是-4.22%；如果按每日收益取均值，再年化，则得到收益是-3.31%，两者相差不大。

接下来，我们获取沪深 300 成份股，以便从中抽取个股进行检验：

import akshare as ak
index_stock_cons_df = ak.index_stock_cons(symbol="399300")
print(index_stock_cons_df)

接下来，我们随机取 10 支股票，获取行情，并计算每日收益率：

np.random.seed(78)

stocks = random.sample(index_stock_cons_df['品种代码'].to_list(), 10)

frames = {}

now = arrow.now()
start = now.shift(years = -1)
end = now.format("YYYYMMDD")
start = start.format("YYYYMMDD")

# 获取 10 支股票的行情数据
for code in stocks:
    bars = ak.stock_zh_a_hist(symbol=code, period="daily", start_date=start, end_date=end, adjust="qfq")
    bars.index = pd.to_datetime(bars["日期"])
    frames[code] = bars["收盘"]

# 与指数行情数据合并
start = np.datetime64(now.shift(years = -1))
frames["399300"] = hs300[hs300.index >= start]["close"]

df = pd.DataFrame(frames)

# 计算每日收益
returns = df.pct_change()

# 如果存在 NAN，则后面的回归法将无法聚合
returns.dropna(how='any', inplace=True)
returns.style.format('{:,.2%}')

计算𝛽¶

我们将通过两种方式来计算𝛽。一种是回归法，一种是协方差法。

回归法¶

在 numpy 中有一个 polyfit 函数，可以用来进行多项式拟合。当我们使用一次项拟合，那么得到的系数就是要求的𝛽。

cols = df.columns
betas = {}
for name in cols:
    beta, alpha = np.polyfit(returns[name], returns["399300"], deg=1)
    print(name, f"{beta:.2%} {alpha:.2%}")
    betas[name] = beta

从结果可以看出，有一支股票存在正的 alpha，同时还存在 10%以上的 beta 收益。

现在，我们就来看看，如果买入这支股票，它们的预期收益应该是多少：

这里要注意，我们使用的 risk_free 是年化收益，因此我们最终计算出来的预期收益，也应该是年化（或者都统一到日化）：

code = "002756"
beta = betas[code]

# 回归法得到的预期收益
expected_return = rf + beta * (market_annual - rf)
print(f"code beta: {beta:.2f}, Er: {expected_return:.2%}")

最终我们得到 002756 的 beta 是 0.11，一年期的预期收益是 1.51%左右。

协方差法¶

params = {}

for name in cols:
    cov = np.cov(returns["399300"], returns[name])
    beta = cov[0,1]/cov[1,1]

    expected_return = rf + beta * (market_annual - rf)
    print(f"{name} beta: {beta:.2%}, Er: {expected_return:.2%}")
    params[name] = beta

beta = params[code]

# 回归法得到的预期收益
expected_return = rf + beta * (market_annual - rf)
print(f"code beta: {beta:.2f}, Er: {expected_return:.2%}")

这样得到 002756 的 beta 是0.11，年化预期收益是1.51%。

可视化¶

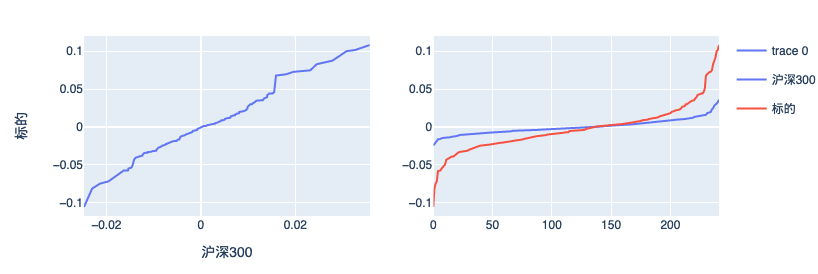
我们可以用下面的方式，将个股与沪深300的涨跌相关性进行可视化，从而得到更直观的印象。

import plotly.graph_objects as go
from plotly.subplots import make_subplots


ci = sorted(set(returns[code].index).intersection(set(returns["399300"].index)))

y = returns[code][ci]
x = returns["399300"][ci]

df = pd.DataFrame({
    "沪深300": sorted(returns["399300"][ci]),
    "标的": sorted(returns[code][ci])
})

fig = make_subplots(
    rows=1,
    cols=2
)

fig.add_trace(go.Scatter(x=df["沪深300"], y=df["标的"]))
fig2 = px.line(df)
fig.add_trace(fig2["data"][0], row=1, col=2)
fig.add_trace(fig2["data"][1], row=1, col=2)

fig['layout']['xaxis']['title']='沪深300'
fig['layout']['yaxis']['title']='标的'

fig.show()

最终我们得到下图：