tools »

原作者失联8个月，我们接手维护后他突然回来了

#python   #quantstats  

---

Table of Content

Quantstats是非常著名的量化策略评估与可视化库。从2024年底起约8个月里，它没有得到积极的维护，出现了在Python 3.12以上，完全无法运行等严重bug。

好消息是，最近一周，原作者 Ran Aroussi 已经恢复了对这个库的维护，并且连发了5个版本（从0.0.64到0.0.68）。

---

我们在课程中一直推荐大家使用这个库来进行策略的评估与可视化，以避免重复造轮子。这种推荐，也使得我们有义务去维护它。于是，我们在7月初发布了quantstats-reloaded。

为避免再次失联，我们仍将继续维护quantstats-reloaded一段时间，以便我们的学员始终能有可用的quantstats。另外，我们也将对这个库进行一些重要的改进，首先是进行单元测试增强。

原库缺乏系统的单元测试和CI，这可能是导致原作者无法及时修复bug的主要原因。

这也让我们作为使用者，不免有些担心。所以，在重启维护之后，我们先借由AI，加上了完整的单元测试与CI流程。然后，我们刚刚手工补齐了最重要的stats模块的全部单元测试，测试结果与原库完全一致（但不一定正确！），并达到了91%的单元测试覆盖率。

以下是我们的对照测试方法。

{code-block} python
df = df.copy()
df['slope'] = (df[factor_col].rolling(slope_window)
                .apply(lambda x: np.polyfit(np.arange(slope_window), x, 1)[0]))

df['signal'] = 0
df.loc[df['slope'] > 0, 'signal'] = 1
df.loc[df['slope'] < 0, 'signal'] = -1

# 计算每日收益率
df['benchmark'] = df['close'].pct_change()

# 计算多空组合收益
df['long_return'] = np.where(df['signal'] == 1, df['benchmark'], 0)
df['short_return'] = np.where(df['signal'] == -1, -df['benchmark'], 0)

# 组合收益 = 多头收益 * 多头权重 + 空头收益 * 空头权重
df['strategy'] = df['long_return'] * long_weight + df['short_return'] * short_weight

return df

如果把signal看成因子，那么这段代码里，因子与远期回报是按时间对齐的，而不是错位对齐的。即，代码把\(T_0\)日的收益归因为\(T_0\)日的因子。而\(T_0\)日收益的确切含义是，你要在\(T_{-1}\)日买入，在\(T_0\)日卖出，才能计算出来。这当然是错误的。

如果今天股价上涨，那么均线的切线就可能方向向上，从而 signal = 1；如果今天股价下跌，均线切线就有可能方向向下，从而 signal = -1。这两种情况都被不合理的计入了组合收益。

Tip

按照研报，它是这样建仓的：

这句话虽然没有包含实现细节，但本质上也是包含了未来数据的，不过它的副作用会小一点：它只是要求在收盘后，根据收盘价计算出来趋势线切线斜率和信号后，再以收盘价买入。

尽管这也有一点点未来数据的含义，但在实践中是允许的，因为理论上你可以赶在尾盘集合竞价时计算信号并买入：这样你计算信号时使用的价格，与最终的收盘价相差并不大，很可能就是一个滑点的价格。在一些回测工具中，也是允许这样做的。比如，backtrader 就允许以当天收盘价买入，只要你声明允许 COC(Cheat on Close)。

修正算法

现在，我们来修正上述代码的错误，我们先考虑能否连带研报中的Cheat on Close这个小小的瑕疵也规避了？

def backtest(df, calc_signal, args, 
             price: str = "open", 
             long_weight: float = 0.5, 
             short_weight: float = 0.5):
    df = df.copy()
    df["signal"] = calc_signal(df, *args)
    df["signal"] = df["signal"].fillna(0)
    df["signal_shifted"] = df["signal"].shift(1)
    df["benchmark"] = df[price].pct_change()

    df['long_return'] = np.where(df['signal_shifted'] == 1, df['benchmark'], 0)
    df['short_return'] = np.where(df['signal_shifted'] == -1, -df['benchmark'], 0)
    df["long_short_return"] = df['long_return'] * long_weight + df['short_return'] * short_weight

    return df

与上一版相比，重要的区别有两点：

1. 我们将信号后移了一行（而不是向前！）。这样在计算仓位时，如果前一天信号为 1，我们就用这个 1 来乘以当天的涨跌幅。
2. 我们允许指定计算收益的价格数据列，默认为 open

如果你熟悉 Alphalens 的话，就会知道它在计算收益时，是以信号发出之后，第二天的开盘价买入，第三天的开盘价卖出来计算 period = 1D 时的收益的。现在，看起来我们正是这样做的！

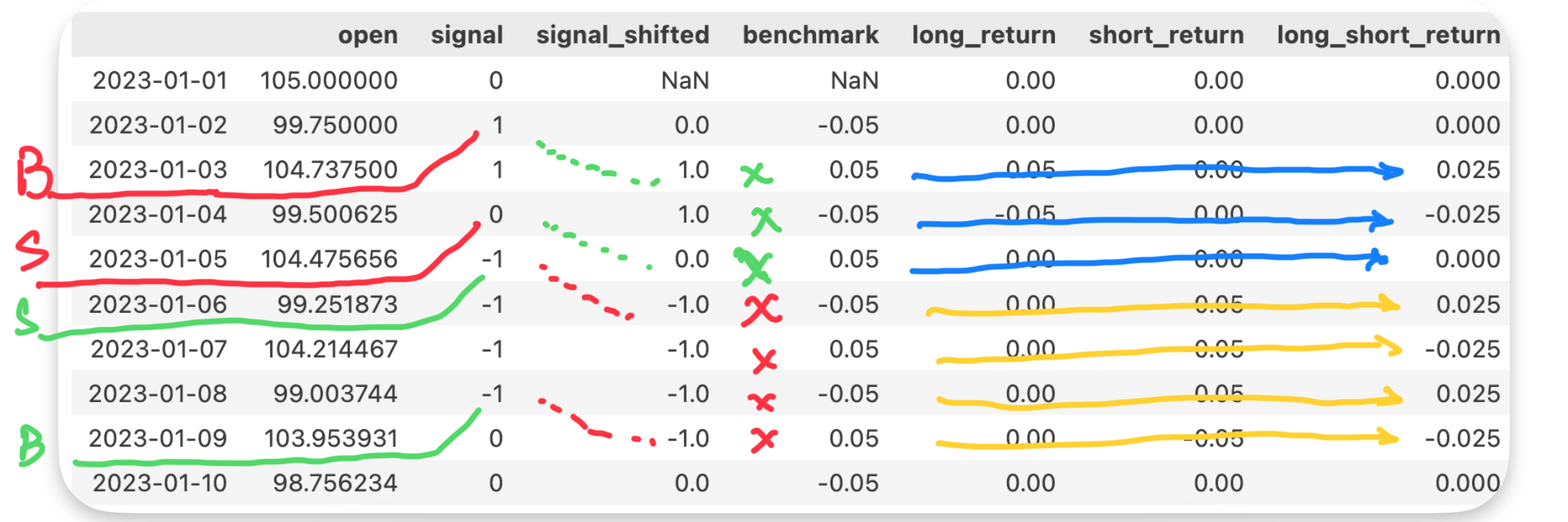
下图显示了最初几次交易的完整过程（使用合成数据，涨跌固定为 5%，-5%交替）：

在 1 月 2 日，策略发出做多信号，于是，我们在 1 月 3 日开盘时多方买入，价格是 104.73，当日涨幅 5%，把 shift 之后的信号 1 作为仓位，最终多空组合收益计为 2.5%（按多、空各可用 50%仓位）。1 月 3 日的信号也为 1，所以持仓中；但当天跌 5%，所以组合收益为-2.5%；4 号的信号为 0，策略需要在 5 日开盘卖出；5 号当天由于不持仓，所以组合的收益为 0。

当使用 open 作为计算收益的价格列之后，我们仍然会得到与之前几乎一样的累积收益图。这次结果可信吗？

看上去都是对的，很完美。除了这一点：在基于 dataframe 的向量化回测框架中，我们不能使用按次日开盘价买入的策略。以1月2日的买入信号为例，由于1月2日的买入信号（1）被移位到了1月3日，算成了多方仓位，所以这会导致把1月3日开盘价对1月2日开盘价的涨幅算成多方收益。而1月2日开盘时，我们还没有实现多方买入呢。

考虑到如果\(T_0\)日以上涨收盘，就更容易发出做多信号，并且次日开盘价也很有可能高于前一日开盘价，所以，这样计算出来的策略收益，会在第一天有较大的作弊成份，这是导致在使用开盘价计算收益时，回测结果很好看的主要原因。

但我们又不能在信号发出后的第三天以开盘价买入（信号不等人！），所以，我们必须使用 Cheat on Close 的策略，也就是价格列必须指定为"close"。

在指定价格列为 close 时，如果记信号发生日为\(T_0\)，信号为 1，由于移位的原因，我们在计算\(T_1\)日的组合收益将是 1 * \(T_1\)日收益，\(T_1\)日的收益是 \(T_1\)日的收盘价与\(T_0\)日的收盘价计算得来的。尽管这是一种 Cheat on Close，但并不会引起太大的误差。

我们使用 DataFrame来进行回测的主要原因是简单快捷。从一个想法到最终实盘，需要经过无数道工序，几个月的时间（以日频计，算上仿真），所以，没有必要一开始就使用更重的框架。如果一个想法在简单测试中就不工作，我们大概率应该放弃它 -- 因为从统计上讲，多数想法本身就是无效的。

backtrader: 慢一点，但是更可靠

对事件型策略的回测，backtrader尽管会慢一点，但是在结果上会更可靠一些，表现在：

1. backtrader默认会在信号发出之后的下一个bar以开盘价买入。
2. backtrader会计算手续费、仓位限制和成交量限制。
3. 基于DataFrame的向量式回测因为很简单，所以没有一个标准的库来实现。我们自己的手工实现比较容易引入错误。

我们就用backtrader来验证一下之前的回测结果。

计算LLT和切线斜率的代码在前一期提供了，这里不再重复。

这是计算llt与切线斜率，生成信号的代码。与前一篇相比，我们增加了thresh参数，将会在调优中使用。

def calculate_llt(prices, alpha=0.05):
    # 转换为numpy数组以避免pandas索引问题
    if hasattr(prices, 'values'):
        prices = prices.values

    n = len(prices)
    llt = np.zeros(n)
    if n >= 1:
        llt[0] = prices[0]
    if n >= 2:
        llt[1] = prices[1]

    a1 = alpha - (alpha**2) / 4
    a2 = (alpha**2) / 2
    a3 = alpha - 3 * (alpha**2) / 4
    a4 = 2 * (1 - alpha)
    a5 = - (1 - alpha)**2

    for t in range(2, n):
        llt[t] = a1 * prices[t] + a2 * prices[t-1] - a3 * prices[t-2] + a4 * llt[t-1] + a5 * llt[t-2]

    return llt

# 信号计算函数
def llt_slope_signal(df, d: int=39, slope_window=5, thresh=(0, 0)):
    df = df.copy()
    alpha = 2 / (d + 1)
    df["llt"] = calculate_llt(df["close"], alpha)
    df['slope'] = (df["llt"].rolling(slope_window)
                    .apply(lambda x: np.polyfit(np.arange(slope_window), x, 1)[0]))

    signals = pd.Series(0, index=df.index)
    signals[df['slope'] > thresh[1]] = 1
    signals[df['slope'] < thresh[0]] = -1
    signals.ffill(inplace = True)

    return signals

Tip

这里对 llt_slope_signal 的参数 d 进行一点说明。它来自于EMA指标公式。当 d 取 9， 19， 39等数值时，对应的 alpha 分别为 0.2, 0.1, 0.05等。

这是回测策略类：

import backtrader as bt
class LLTStrategy(bt.Strategy):
    params = (
        ('d', 39),
        ('slope_window', 5), 
        ('position_ratio', 1),
        ('thresh', (0, 0))
    )

    def __init__(self):
        self.order_dict = {}
        self.signals = llt_slope_signal(
            self.data._dataname,
            d=self.p.d,
            slope_window=self.p.slope_window,
            thresh=self.p.thresh
        )

        self._last_direction = 0

        print(f"策略初始化完成，信号数量: {len(self.signals)}")
        print(f"信号前20个值: {self.signals.head(20)}")

    def next(self):
        current_date = pd.Timestamp(self.data.datetime.date())

        current_signal = self.signals.loc[current_date]
        position = self.getposition(self.data).size

        if current_signal != 0:
            print(f"日期: {current_date}, 信号: {current_signal}, 当前持仓: {position}")

        if current_signal == 1 and self._last_direction <= 0:
            order = self.order_target_percent(target=0.95)
            if order:
                print(f"做多信号: {current_date.date()}")
        elif current_signal == -1 and self._last_direction >= 0:
            order = self.order_target_percent(target=-0.95)
            if order:
                print(f"做空信号: {current_date.date()}")
        elif current_signal == 0 and position != 0:
            order = self.order_target_percent(target=0.0)
            if order:
                print(f"平仓信号: {current_date.date()}")
        else:
            pass

我们省略回测调用代码，以节省篇幅。如果你需要这些代码，可以购买匡醍会员。如果你不太理解我们在讨论些啥，你应该报名匡醍的《量化24课》和《因子挖掘与机器学习策略》。

def run_backtest(data, d=39, 
                 slope_window=5, 
                 thresh=(0,0),
                 initial_cash=1_000_0000, 
                 commission=1e-4):
    cerebro = bt.Cerebro()

    cerebro.broker.setcash(initial_cash)
    cerebro.broker.setcommission(commission=commission)

    cerebro.addstrategy(LLTStrategy, d=d, slope_window=slope_window, thresh=thresh)

    bt_data = bt.feeds.PandasData(dataname=data)
    cerebro.adddata(bt_data)

    # 添加绩效分析器
    cerebro.addanalyzer(bt.analyzers.SharpeRatio, _name='sharpe')
    cerebro.addanalyzer(bt.analyzers.DrawDown, _name='drawdown')
    cerebro.addanalyzer(bt.analyzers.Returns, _name='returns')

    # 运行回测
    print(f"初始资金: {cerebro.broker.getvalue():.2f}")
    results = cerebro.run()
    final_value = cerebro.broker.getvalue()
    print(f"最终资金: {final_value:.2f}")

    # 输出绩效指标
    strat = results[0]
    returns = strat.analyzers.returns.get_analysis()
    sharpe = strat.analyzers.sharpe.get_analysis()
    drawdown = strat.analyzers.drawdown.get_analysis()

    print(f"夏普比率: {sharpe.get('sharperatio', 0):.2f}")
    print(f"最大回撤: {drawdown.get('max', {}).get('drawdown', 0):.2f}%")
    print(f"年化收益率: {returns.get('rnorm', 0):.2%}")

    return returns.get('rnorm', 0), sharpe.get('sharperatio', 0), drawdown.get('max',{}).get('drawdown',0)


def get_price(symbol, start_date, end_date):
    pro = pro_api()

    price_df = pro.index_daily(
        ts_code=symbol,
        start_date=start_date.strftime("%Y%m%d"),
        end_date=end_date.strftime("%Y%m%d"),
    )

    price_df = (
        price_df.rename({"trade_date": "date", "ts_code": "asset"}, axis=1)
        .sort_values("date", ascending=True)
        .set_index("date")
    )

    price_df.index = pd.to_datetime(price_df.index)
    return price_df

start = datetime.date(2005, 9, 6)
end = datetime.date(2013, 6, 28)
prices= get_price("000001.SH", start, end)

run_backtest(prices, commission = 1e-3)

我们得到的结果是，年化收益11.8%，夏普0.4。会比基准略好一点。但是，如果我们对2013年之后的区间进行回测，会发现我们其实只是捡回来一条咬人的毒蛇：

start = datetime.date(2013, 1, 1)
end = datetime.date(2024, 12, 31)
prices= get_price("000001.SH", start, end)

run_backtest(prices, commission=1e-3)

这次的年化是-6.4%，最大回撤79%。

backtrader参数优化

我们应该对此失望吗？

不！我们从来就不应该指望一个简单的策略，甚至只有不到 100 行代码，就能成为一台印钞机。繁复深奥并不必然成功，但在资本市场上，简单甚至简陋肯定是不行的。任何赚钱的生意，都必须有壁垒。

所以，我们的优化之路刚刚开始。远远不到应该失望的时候！

首先，千分之一的手续费太高了。当我们在指数上回测时，一定要记住指数本身就没有太大的盈利空间，任何跑冒滴漏都不能允许！

现在，多数券商的交易手续费，特别是量化交易的，已经低到万分之 0.854 了。所以，我们完全没必要设置千分之一这么高的手续费。

Info

当我们把佣金调到万分之一时（仍高于市场），年化收益率就提升到了-3.7%。已经好多了。我们会在后面的测试中，使用这个设置。不过，这并不是策略优化。真正的优化，马上开始！

在仔细分析之后，我们发现信号翻转过于频繁。当切线斜率从-0.01 变化为 0.005 时，我们就要从空单马上变为多单？这显然不合理，我们应该过滤掉这种虚假的信号。切线斜率的计算本身，也受到 alpha 的影响。我们之前的回测中，使用的是 0.05,它会是最优的吗？

我们决定使用 backtrader 自带的参数优化方案来帮我们调优。但是，调优可能出现过拟合，所以，我们最后还要分享如何判断调优的结果没有过拟合。

我们先来定义优化函数。

from IPython.display import clear_output
def optimize(data, d, thresh):
    cerebro = bt.Cerebro()

    cerebro.broker.setcash(1_000_0000)
    # 万分之一的佣金。现在多数券商给到了万分之 0.854
    cerebro.broker.setcommission(commission=0.0001)

    bt_data = bt.feeds.PandasData(dataname=data)
    cerebro.adddata(bt_data)

    # 添加绩效分析
    cerebro.addanalyzer(bt.analyzers.Returns, _name='returns')

    cerebro.optstrategy(LLTStrategy, d = d, thresh = thresh)
    strats = cerebro.run(maxcpus = 1, optreturn = True)

    clear_output()

    params_and_returns = []
    for s in strats:
        returns = s[0].analyzers.returns.get_analysis()
        d, thresh = s[0].params.d, s[0].params.thresh[0]

        rnorm, pnl = f"{returns['rnorm']:.2%}", f"{returns['rtot']:.2%}"
        params_and_returns.append((d, thresh, rnorm, pnl))

    return pd.DataFrame(params_and_returns, columns=["d", "thresh", "rnorm", "pnl"])

start = datetime.date(2008, 1, 1)
end = datetime.date(2012, 12, 31)
prices= get_price("000001.SH", start, end)

result = optimize(prices, 
                  (9, 19, 39, 49, 59), 
                  (
                    (-0.01, 0.01), 
                    (-0.02, 0.02), 
                    (-0.04, 0.04), 
                    (-0.08, 0.08), 
                    (-0.12, 0.12)
                  ))
result

通过backtrader来进行参数优化，关键是这样两行代码：

{code-block} python
    cerebro.optstrategy(LLTStrategy, d = d, thresh = thresh)
    strats = cerebro.run(maxcpus = 1, optreturn = True)

在 notebook 中运行时，我们必须设置maxcpus = 1。如果maccpus > 1，将会启动多进程优化。此时涉及到notebook中代码的持久化（因为要把代码传送到新的进程中），就会出错。

我们在《量化24课》中，详细介绍了如何使用backtrader，也包括了策略优化。

我们让参数 d 在 (9, 19, 39, 49, 59, 69),之间取值，这样对应的alpha会是(0.2， 0.1， 0.05， 0.03)，而thresh则在(-0.01, 0.01)到(-0.12, 0.12)之间，以倍增的方式来取值。

参数优化

为了视觉上美观，这里只筛选了部分结果。

从参数优化结果来看，d = 59, thresh = -0.01 是最好的一组，达到了年化26.6%的超高收益率。总体来看，随着 d 值增加，收益变好；thresh的影响并不大。另外，还有一个对性能有影响的参数，即计算切线斜率时，使用多少个 bar? 这里只使用了固定的 5。

刚刚的参数优化是基于2008年到2012年的数据得到的。它在2005年到2013年间的情况怎么样？结论是：年化收益率达到了25.6%。

如果我们把这个参数用于2013年到2014年的投资，那么，将会得到13.9%的年化和0.97的夏普率。这个成绩应该说相当不错。

正确看待过拟合

当我们使用backtrader来进行参数优化时，一定要注意会比较容易出现过拟合。

在上一节，我们已经把基于[2008,2012]得到的最优参数，运用于过去[2005, 2012]和未来[2013,2014]，来对比观察结果。这是检验过拟合是否存在的一种方法。如果参数没有过拟合，那么它就应该在它没有见过的数据上，也能讲出好的故事出来。

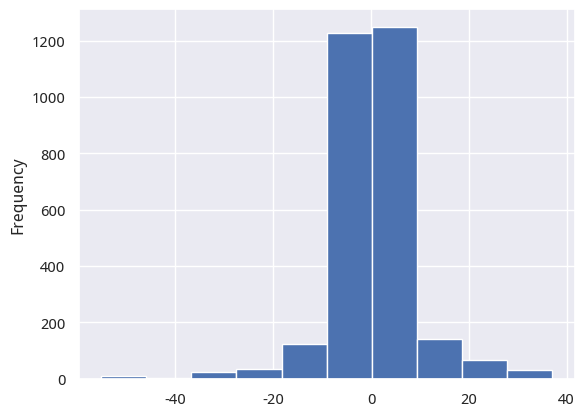
这里还介绍另外一个思路。关于thresh参数的。基于 thresh 来决定 signal，显然要比简单地基于 0 来判断 signal 合理，这一点无庸置疑。但优化的thresh参数会不会导致过拟合？这时候我们可以观察下切线斜率的分布：

def llt_slope(df, d: int=59, slope_window=5):
    df = df.copy()
    alpha = 2 / (d + 1)
    df["llt"] = calculate_llt(df["close"], alpha)
    df['slope'] = (df["llt"].rolling(slope_window)
                    .apply(lambda x: np.polyfit(np.arange(slope_window), x, 1)[0]))

    return df['slope']

start = datetime.date(2005, 1, 1)
end = datetime.date(2013, 12, 31)
prices= get_price("000001.SH", start, end)

slopes = llt_slope(prices, d = 39)
slopes.plot(kind='hist')
s1 = (slopes < -0.02).sum()/len(slopes)
s2 = (slopes < 0.02).sum()/len(slopes)

s2 - s1

切线斜率分布

可以看出，通过设置 thresh 为 [-0.02, 0.02]，我们只排除了 0.3%左右的数据。这说明：我们并没有通过 hacking 的手段，排除大多数情形，只留下让最终收益好看的少量数据。因此，至少在thresh参数上，很有可能这里并没有发生过拟合。

如果我们通过[2008, 2012]年的数据优化出来的参数 d = 59, thresh = [-0.01, 0.01] 用在2013年到2024年不变的话，那么年化收益率会衰减到2.79%。这说明，市场风格其实是一直在变化的。这个策略也只是一个\(\beta\)因子。

不过，我们可以每隔几年就更新一次参数，再在接下来的一小段时间内，使用这个策略。

下面的代码演示了如何基于过去5年的数据搜索出优化参数，然后用在随后两年的投资中：

```python