papers »
『匡醍译研报 02』 驯龙高手,从股谚到量化因子的工程化落地
上一期文章中,我们复现了研报的因子构建部分,分别是影线因子、威廉影线因子以及由此组合而来的 UBL 因子。这一期我们将对这些因子进行检验。
因子检验固然是因子挖掘中必不可少的一环,但它应该是一个 routine 的工作 -- 我们不应该每次都重新发明轮子。然而,当我们使用Alphalens 来进行因子检验时,令人尴尬的事情发生了。
Alphalens 请就位
Alphalens 是一个基于 pandas 的开源库,它提供了一系列的函数,用于对因子进行分析和评估。一直以来是因子检验的不二之选。
所以,我们先拿上影线标准差因子来试试。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 def calculate_shadow_ratio ( bars ):
"""计算上下影线因子(归一化)
按研报要求,标准化蜡烛上影线为当日上影线/过去 5 日上影线均值。标准化蜡烛下影线同。
"""
high = bars [ 'high' ]
low = bars [ 'low' ]
open_price = bars [ 'open' ]
close = bars [ 'close' ]
# 为避免除零错误,这里我们使用了一个技巧,即通过 mask 来排除可能除零的计算
# 无法计算时,设置为 0,表明无信号
up_shadow_ratio = pd . Series ( 0 , index = bars . index )
down_shadow_ratio = pd . Series ( 0 , index = bars . index )
up_shadow = high - np . maximum ( open_price , close )
rolling_up_shadow = up_shadow . rolling ( 5 ) . mean ()
mask = rolling_up_shadow > 1e-8
up_shadow_ratio [ mask ] = up_shadow [ mask ] / rolling_up_shadow [ mask ]
down_shadow = np . minimum ( open_price , close ) - low
rolling_down_shadow = down_shadow . rolling ( 5 ) . mean ()
mask = rolling_down_shadow > 1e-8
down_shadow_ratio [ mask ] = down_shadow [ mask ] / rolling_down_shadow [ mask ]
return up_shadow_ratio , down_shadow_ratio
def calc_monthly ( daily_factor , aggfunc , win = 20 ):
dates = daily_factor . index . get_level_values ( 'date' ) . unique () . sort_values ()
month_ends = dates . to_frame ( name = "date" ) . resample ( 'BME' ) . last () . values
dfs = []
for date in month_ends :
date_ts = pd . Timestamp ( date . item ())
iend = dates . get_loc ( date_ts )
istart = max ( 0 , iend - win + 1 )
start_ = pd . Timestamp ( dates [ istart ])
end_ = date_ts
window_data = daily_factor . loc [ start_ : end_ ]
df = ( window_data . groupby ( level = "asset" )
. agg ( aggfunc )
. to_frame ( "factor" )
)
df [ "date" ] = date_ts
dfs . append ( df )
df = pd . concat ( dfs )
return df . set_index ([ "date" , df . index ]) . sort_index ()
def calc_candle_up_std_factor ( barss , win = 20 ):
up_shadow = barss . groupby ( "asset" , group_keys = False ) . apply ( lambda x : calculate_shadow_ratio ( x )[ 0 ]) . sort_index ()
return calc_monthly ( up_shadow , "std" , win )
这些都是上一期介绍过的代码。下面,我们就来调用 Alphalens 进行测试:
Attention
from alphalens.performance import factor_alpha_beta
start = datetime . date ( 2009 , 1 , 1 )
end = datetime . date ( 2020 , 4 , 30 )
barss = load_bars ( start , end , 50 )
up_std_factor = calc_candle_up_std_factor ( barss , 20 )
prices = barss [ "price" ] . unstack ( level = 1 )
merged = get_clean_factor_and_forward_returns ( up_std_factor , prices , quantiles = 5 )
alpha = factor_alpha_beta ( merged )
alpha
from alphalens.performance import factor_alpha_beta
start = datetime . date ( 2009 , 1 , 1 )
end = datetime . date ( 2020 , 4 , 30 )
barss = load_bars ( start , end , 50 )
up_std_factor = calc_candle_up_std_factor ( barss , 20 )
prices = barss [ "price" ] . unstack ( level = 1 )
merged = get_clean_factor_and_forward_returns ( up_std_factor , prices , quantiles = 5 )
alpha = factor_alpha_beta ( merged )
alpha
不出意外的话,意外就会发生了。Alphalens 会抛出一个异常:
Warning
不要慌! 这段代码注定应该报错。
File ~/ miniforge3 / envs / zillionare / lib / python3 .12 / site - packages / pandas / core / arrays / datetimelike . py : 2162 , in TimelikeOps . _validate_frequency ( cls , index , freq , ** kwargs )
2156 raise err
-> 2162 raise ValueError (
2163 f "Inferred frequency { inferred } from passed values "
2164 f "does not conform to passed frequency { freq . freqstr } "
2165 ) from err
ValueError : Inferred frequency None from passed values does not conform to passed frequency C
calc_candle_up_std_factor 函数返回的数据,只包含每个月末的日期,Alphalens 无法从中推断出交易日历,因此抛出了异常。
Tip
Alphalens 在进行因子收益分析时,需要先计算远期收益。远期收益由用户通过参数periods指定,默认为 [1, 5, 10]。periods 的单位默认是「Day」,因此它期待一个在日期上连续的索引。由于我们传入的数据只包含每个月末的日期,所以就得到了这样一个异常。
从根本上说,Alphalens 无法处理按月调仓的策略。Alphalens 推荐的一个变通方案是,你可以按日计算因子,再指定periods参数为 [21, 105, 210],这样来模拟按 1 个月、5 个月和 10 个月来计算远期收益。但是,它推荐的变通方案也不见得可行,因为不是每个月都刚好 21 个交易日。
介绍一位新人
考虑到月度因子检验在研报中非常常见,我们决定自己开发一个简单的回测库,专门处理月度因子,它将实现这样的功能:对每一个在月末有数据的资产,我们将在次日初以开盘价买入,在月末以收盘价卖出,并计算其收益。
Tip
另一个常用的快速检验框架是vectorbt,理论上它可以实现月初买入、月末卖出的逻辑,不过都依赖于个人实现。
代码有点长,核心逻辑都在下面这两个函数里面:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122 def _monthly_factor_backtest (
factor_data : "pd.Series[float]" ,
bars : pd . DataFrame ,
quantiles : Optional [ int ] = 5 ,
bins : Optional [ Union [ int , List [ float ]]] = None ,
factor_lag : int = 1 ,
weighting_method : str = "equal_weight" ,
) -> Tuple [
pd . DataFrame , "pd.Series[float]" , "pd.Series[float]" , "pd.Series[float]"
]:
"""
Monthly Factor Backtesting Framework
策略逻辑:
1. 基于上月末因子值对股票分组
2. 在下月初买入,下月末卖出
3. 计算各组合的月度收益率
如果因子值或者价格数据在交易日期(月初或者月末)缺少数据,该资产将被从组合中排除。这有可能导致回测数据不足。因此,推荐做法是您确保传入的因子数据和价格数据,都包含所有交易日期的数据。
Returns:
tuple: (策略分组月度收益 DataFrame, 基准月度收益 Series, long-only 收益 Series, 多空组合收益 Series, IC 序列 Series)
策略收益以月份为索引,分组为列
基准收益为所有股票等权重收益
纯多和多空组合收益根据 weighting_method 计算
IC 序列为每月因子值与收益率的相关系数
"""
# 重置索引便于操作
factor_df = factor_data . to_frame ( name = "factor" ) . reset_index ()
factor_col = "factor"
bars_df = bars . reset_index ()
# 转换日期列为 datetime 类型
factor_df [ "date" ] = pd . to_datetime ( factor_df [ "date" ])
bars_df [ "date" ] = pd . to_datetime ( bars_df [ "date" ])
# 构建交易日历
trading_calendar = _build_trading_calendar ( bars_df )
# 为因子数据添加年月信息
factor_df [ "year_month" ] = factor_df [ "date" ] . dt . to_period ( "M" )
# 存储月度收益
monthly_returns = []
benchmark_returns = []
long_only_returns = []
long_short_returns = []
ic_values = []
# 遍历交易日历,执行回测
for i in range ( factor_lag , len ( trading_calendar )):
current_trading_month = trading_calendar . iloc [ i ]
factor_month = trading_calendar . iloc [ i - factor_lag ]
# 处理单个月的回测逻辑
result = _process_single_month (
current_trading_month = current_trading_month ,
factor_month = factor_month ,
factor_df = factor_df ,
bars_df = bars_df ,
factor_col = factor_col ,
quantiles = quantiles ,
bins = bins ,
weighting_method = weighting_method ,
)
if result is not None :
(
group_returns ,
benchmark_return ,
long_only_return ,
long_short_return ,
ic_value ,
) = result
monthly_returns . append ( group_returns )
benchmark_returns . append ( benchmark_return )
long_only_returns . append ( long_only_return )
long_short_returns . append ( long_short_return )
ic_values . append ( ic_value )
# 合并所有月份的收益
if not monthly_returns :
return pd . DataFrame (), pd . Series (), pd . Series (), pd . Series (), pd . Series ()
# 策略收益
quantile_returns = pd . concat ( monthly_returns , axis = 1 ) . T
quantile_returns . index = cast (
pd . PeriodIndex , quantile_returns . index
) . to_timestamp ( how = "end" , freq = "D" )
# 重命名列
if quantiles is not None :
quantile_returns . columns = [ f "Q { i } " for i in quantile_returns . columns ]
else :
quantile_returns . columns = [ f "Bin { i } " for i in quantile_returns . columns ]
# 基准收益
benchmark_series = pd . Series (
benchmark_returns , index = quantile_returns . index , name = "Benchmark"
)
# long-only 收益
long_only_series = pd . Series (
long_only_returns , index = quantile_returns . index , name = "Long_Only"
)
# 多空组合收益
long_short_series = pd . Series (
long_short_returns , index = quantile_returns . index , name = "Long_Short"
)
# IC 序列
ic_series = pd . Series ( ic_values , index = quantile_returns . index , name = "IC" )
return (
quantile_returns ,
benchmark_series ,
long_only_series ,
long_short_series ,
ic_series ,
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100 def _process_single_month (
self ,
current_trading_month : "pd.Series[Any]" ,
factor_month : "pd.Series[Any]" ,
factor_df : pd . DataFrame ,
bars_df : pd . DataFrame ,
factor_col : str ,
quantiles : Optional [ int ] = None ,
bins : Optional [ Union [ int , List [ float ]]] = None ,
weighting_method : str = "equal_weight" ,
) -> Optional [ Tuple [ "pd.Series[float]" , float , float , float , float ]]:
"""
处理单个月的回测逻辑
"""
# 获取因子计算时点的数据(通常是月末)
factor_date = factor_month [ "month_end" ]
factor_month_data = factor_df [( factor_df [ "date" ] == factor_date )] . copy ()
if len ( factor_month_data ) == 0 :
return None
# 买入价格(当月月初开盘价)
buy_date = current_trading_month [ "month_start" ]
buy_prices = bars_df [ bars_df [ "date" ] == buy_date ][[ "asset" , "open" ]] . copy ()
buy_prices . columns = [ "asset" , "price_buy" ]
# 卖出价格(当月月末收盘价)
sell_date = current_trading_month [ "month_end" ]
sell_prices = bars_df [ bars_df [ "date" ] == sell_date ][[ "asset" , "close" ]] . copy ()
sell_prices . columns = [ "asset" , "price_sell" ]
if len ( buy_prices ) == 0 or len ( sell_prices ) == 0 :
return None
# 合并数据
month_data = factor_month_data . merge ( buy_prices , on = "asset" , how = "inner" )
month_data = month_data . merge ( sell_prices , on = "asset" , how = "inner" )
# 移除缺失数据的股票
month_data = month_data . dropna ( subset = [ factor_col , "price_buy" , "price_sell" ])
if len ( month_data ) == 0 :
return None
# 因子分组
try :
if quantiles is not None :
month_data [ "group" ] = (
pd . qcut (
month_data [ factor_col ],
q = quantiles ,
labels = False ,
duplicates = "drop" ,
)
+ 1
)
else :
assert bins is not None , "bins 不能为 None"
month_data [ "group" ] = (
pd . cut (
month_data [ factor_col ],
bins = bins ,
labels = False ,
include_lowest = True ,
)
+ 1
)
except ValueError :
# 如果因子值相同导致无法分组,跳过该月
return None
# 计算个股收益率
month_data [ "return" ] = month_data [ "price_sell" ] / month_data [ "price_buy" ] - 1
# 计算各组等权重收益率(保持原有逻辑)
group_returns = month_data . groupby ( "group" )[ "return" ] . mean ()
# 计算基准收益率(所有股票等权重)
benchmark_return = month_data [ "return" ] . mean ()
# 计算 long-only 和多空组合收益率
long_only_return , long_short_return = self . _calculate_portfolio_returns (
month_data , group_returns , factor_col , weighting_method
)
# 计算 IC 值(因子值与收益率的相关系数)
ic_value = month_data [ factor_col ] . corr ( month_data [ "return" ])
if pd . isna ( ic_value ):
ic_value = 0.0
# 添加月份信息
group_returns . name = current_trading_month [ "year_month" ]
return (
group_returns ,
benchmark_return ,
long_only_return ,
long_short_return ,
ic_value ,
)
最核心的部分,是通过价格数据,重采样出月度日历(有月头和月尾日期),然后就可以遍历因子,对每一个 T0 月末因子,找到对应的下一个月月头,以开盘价买入,以下一个月月尾的收盘价卖出,这样得到的收益,就是 T0 期因子的月度收益。
最后,我们返回分组月收益,基准月收益、多空对冲收益,单多月收益和 IC。
在使用上,moonshot非常简单。
我们先造一点数据,再来演示。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 def key_frames ( bars , dates ):
df = dates . to_frame ( name = "date" )
month_starts = df . resample ( 'MS' )[ 'date' ] . first ()
month_ends = df . resample ( 'BME' )[ 'date' ] . last ()
key_frames = bars [
( bars . index . get_level_values ( 0 ) . isin ( month_ends ) |
bars . index . get_level_values ( 0 ) . isin ( month_starts ))
]
return key_frames
factor_data = [
( pd . Timestamp ( '2023-01-31' ), "A" , 1.0 ),
( pd . Timestamp ( '2023-01-31' ), "B" , 2.0 )
]
factor_df = pd . DataFrame ( factor_data ,
columns = [ "date" , "asset" , "factor" ]) . set_index ([ "date" , "asset" ])
dates = pd . date_range ( '2023-01-01' , '2023-02-28' , freq = 'D' )
prices = [( "A" , 100 , 110 ), ( "B" , 100 , 105 )] * len ( dates )
bars = pd . DataFrame ( prices , columns = [ "asset" , "open" , "close" ],
index = np . repeat ( dates , 2 ))
bars = bars . set_index ([ bars . index , 'asset' ])
bars . index . names = [ "date" , "asset" ]
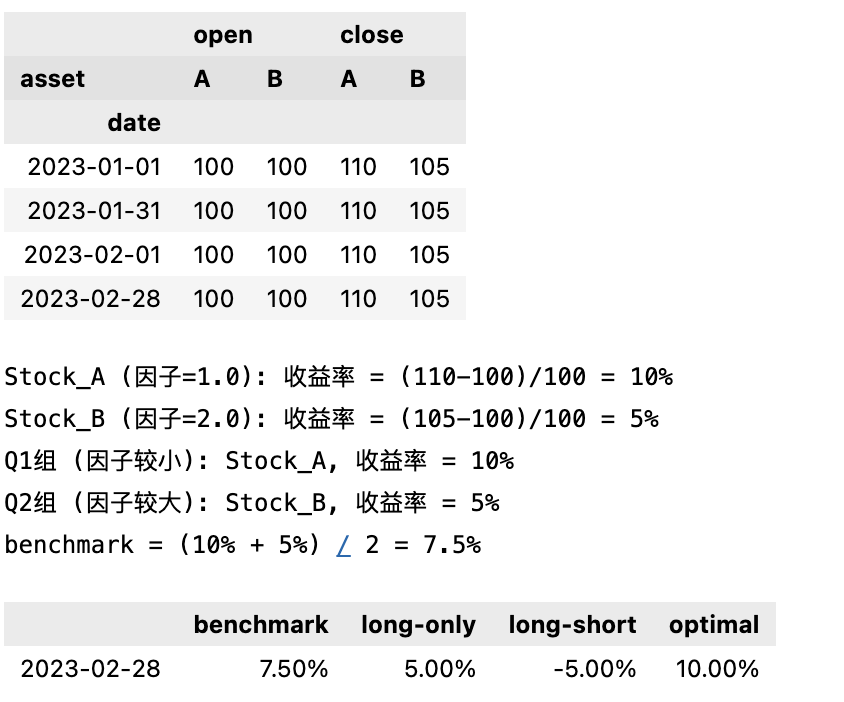
display ( key_frames ( bars , dates ) . unstack ())
print ( "Stock_A (因子=1.0): 收益率 = (110-100)/100 = 10%" )
print ( "Stock_B (因子=2.0): 收益率 = (105-100)/100 = 5%" )
print ( "Q1组 (因子较小): Stock_A, 收益率 = 10%" )
print ( "Q2组 (因子较大): Stock_B, 收益率 = 5%" )
print ( "benchmark = (10 % + 5% ) / 2 = 7.5%" )
expected = pd . DataFrame ([[ 0.075 , 0.05 , - 0.05 , 0.1 ]],
columns = [ "benchmark" , "long-only" , "long-short" , "optimal" ], index = [ "2023-02-28" ])
expected . style . background_gradient ( cmap = 'RdYlGn' )
expected . style . format ( " {:.2%} " )
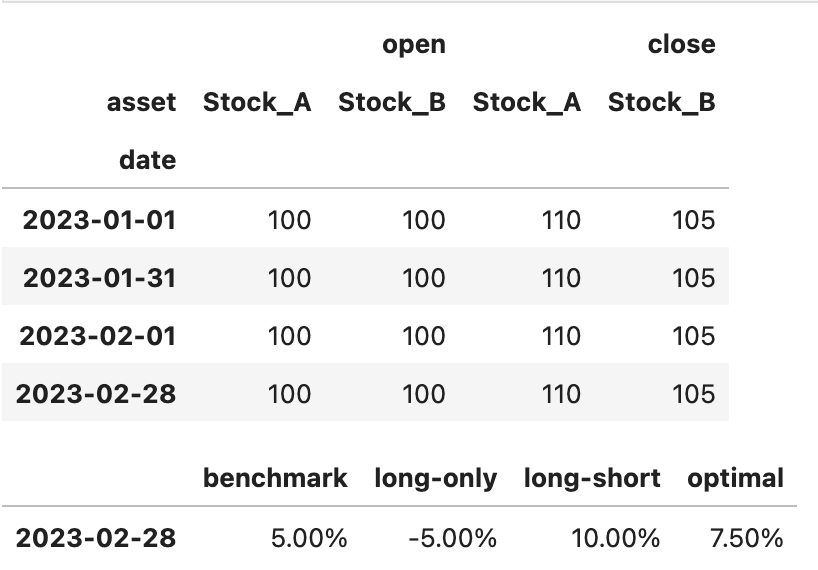
下面是数据及期望值:
回测和结果可视化只要三行代码:
1
2
3
4
5
6
7
8
9
10
11
12
13 from moonshot import Moonshot
moonshot = Moonshot ()
# 执行回测(使用2个分位数)
moonshot . backtest ( factor_df , bars , quantiles = 2 )
actual = pd . DataFrame ([ moonshot . benchmark_returns ,
moonshot . long_only_returns ,
moonshot . long_short_returns ,
moonshot . optimal_returns ]) . T
actual . columns = [ "benchmark" , "long-only" , "long-short" , "optimal" ]
actual . style . format ( " {:.2%} " )
研报结论能否复现?
掌握了回测工具的用法之后,现在,我们就来回答最关键的问题:研报提出的因子,能否复现?我们将使用 moonshot 来进行因子检验。
蜡烛上影线标准差因子
我们先看看蜡烛上影线标准差因子:
start = datetime . date ( 2009 , 1 , 1 )
end = datetime . date ( 2020 , 4 , 30 )
barss = load_bars ( start , end , 50 )
factor = calc_candle_up_std_factor ( barss , 20 )
ms = Moonshot ()
ms . backtest ( factor , barss )
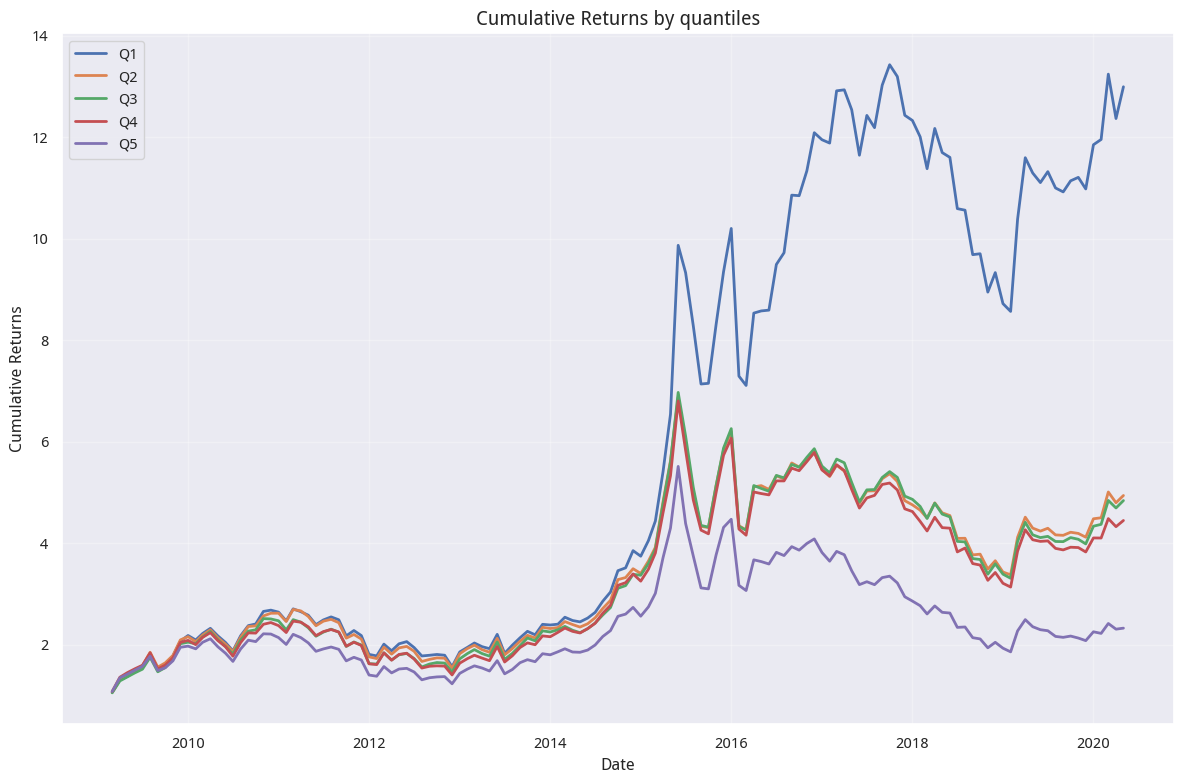
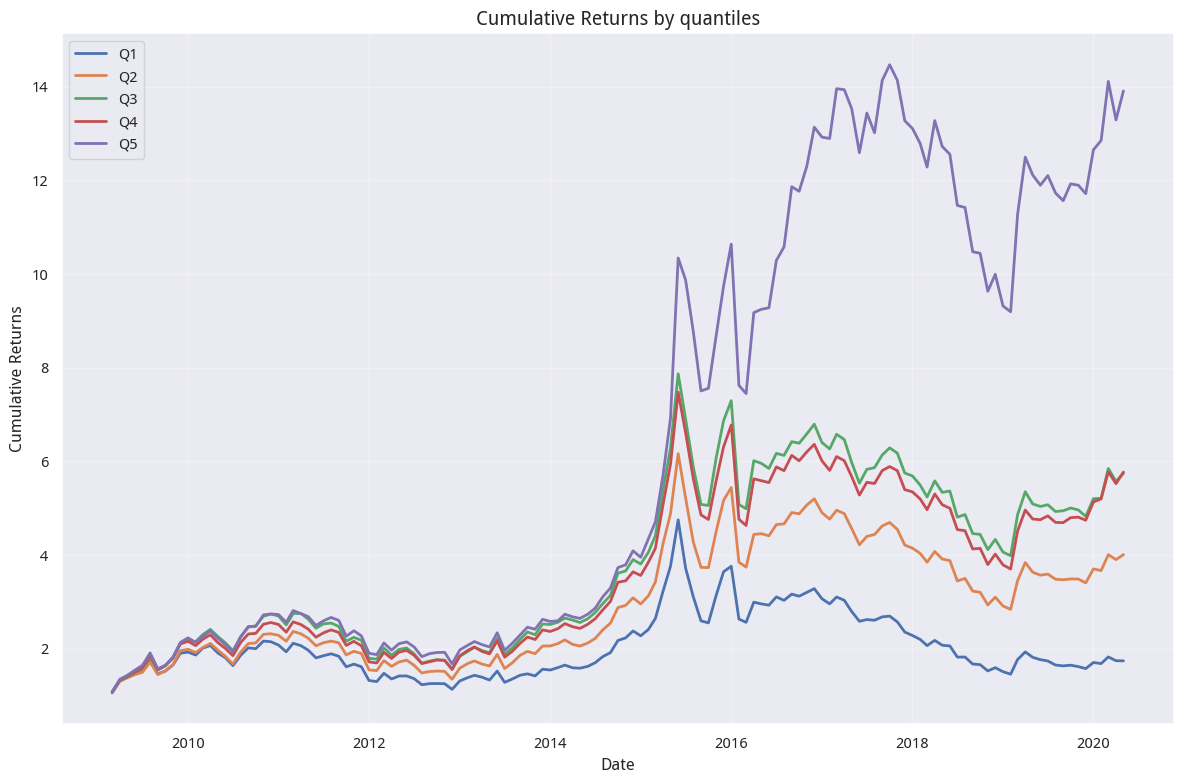
ms . plot_cumulative_returns_by_quantiles ()
尽管我们只用了 50 支个股来进行回测,如果将 universe 参数改为 3000,效果也仍然会很好。
从结果上来看相当不错!几乎与研报报告的一致。当然,如果你熟悉因子检验的基础理论,你就会知道,这个因子实际上是一个反向因子 -- 也就是它是很好的『见顶指标』。
为何我们的结果更好
从收益图看,这里的结果会比研报更好一些。有三个原因,第一是moonshot没有计算手续费;其次,我们无法精准地复现研报回测时使用的 universe。第三点,完全复现研报很困难,因为有很多技术细节会在写研报时被省略。
威廉下影线均线因子
我们再看看威廉下均线因子的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 from moonshot import Moonshot
def calculate_williams_r_ratio ( bars ):
"""
计算变种威廉指标
"""
high = bars [ 'high' ]
low = bars [ 'low' ]
close = bars [ 'close' ]
wr_up = high - close
wr_down = close - low
rolling_wr_up = wr_up . rolling ( 5 ) . mean ()
rolling_wr_down = wr_down . rolling ( 5 ) . mean ()
# 与蜡烛上下影线的默认值不同,0.5 更能表明无信号的含义
wr_up_ratio = pd . Series ( 0.5 , index = bars . index )
wr_down_ratio = pd . Series ( 0.5 , index = bars . index )
mask = rolling_wr_up > 1e-8
wr_up_ratio [ mask ] = wr_up [ mask ] / rolling_wr_up [ mask ]
mask = rolling_wr_down > 1e-8
wr_down_ratio [ mask ] = wr_down [ mask ] / rolling_wr_down [ mask ]
return wr_up_ratio , wr_down_ratio
def calc_wr_down_factor ( barss , win = 20 ):
wr_down = ( barss . groupby ( "asset" , group_keys = False )
. apply ( lambda x : calculate_williams_r_ratio ( x )[ 1 ])
. sort_index ())
return calc_monthly ( wr_down , "mean" , win )
start = datetime . date ( 2009 , 1 , 1 )
end = datetime . date ( 2020 , 4 , 30 )
barss = load_bars ( start , end , 50 )
factor = calc_wr_down_factor ( barss , 20 )
ms = Moonshot ()
ms . backtest ( factor , barss )
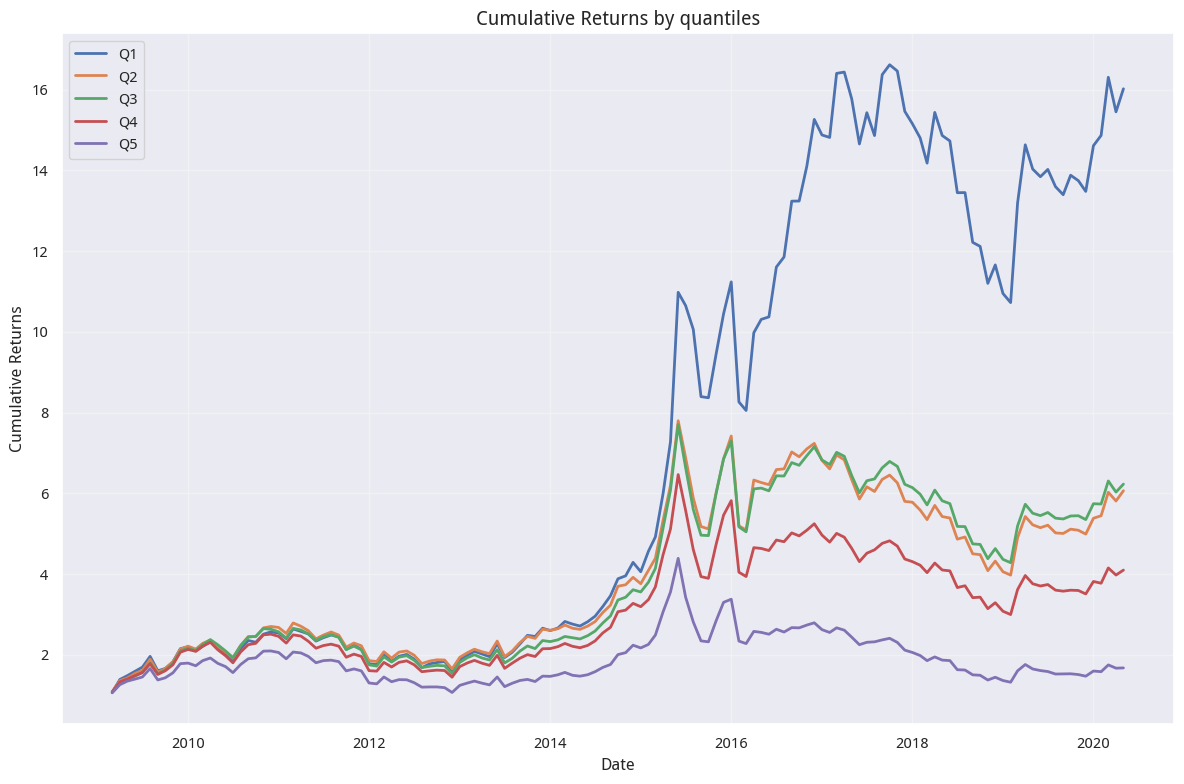
ms . plot_cumulative_returns_by_quantiles ()
这张图证实了研报所说,威廉下均线因子也是个很好的选股因子。不过,你们看出来了吗?下影线均值越小,后市上涨概率越高。这个结果会不会有点反直觉?并且,这与研报开题时的陈述也似乎不太一致。
在研报开头,作者提到,威廉下影线越长,买气越足,后期看涨;反之,后期看跌,并且举了上证指数在2020年2月3日和2020年2月4日的例子。这是怎么一回事呢?
Tip
在读到这期研报之前,我的直觉经验告诉我,下影线越长,往往意味着买方力道大于卖方力道,越有可能反转。但看到这个结果之后,我重新思考了我的经验。我的经验部分是对的;但这也是主观与量化之间最明确的分野:我们的主观记忆只会留下少数幸福或者痛苦的时刻,却主动『遗忘』大量平凡的日子。但可能从统计上看,那些平凡的日子,在复利的作用下,才是引导我们走上人生顶峰的路标。
从量化人的角度来看,威廉下影线_mean 因子值低,表明过去一段时间内,股票经常以接近最低价收盘。这种情况往往出现在 超跌反弹 的前夜。当股票持续承压,多次以低位收盘后,往往蕴含着 均值回归 的机会。市场情绪过度悲观时,正是价值投资者入场的时机。这可能是对这种反常现象一种解读吧。
相反,第五组因子值最高,意味着股票经常以接近最高价收盘,这可能暗示 追高风险 较大,后续上涨空间有限。
UBL因子
那么研报将这两种因子进行组合的一,得到的因子,效果又将如何?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 def calc_ubl_factor ( barss , win = 20 ):
from scipy.stats import zscore
up_std = calc_candle_up_std_factor ( barss , win )
wr_down = calc_wr_down_factor ( barss , win )
# 截面 zscore
z_scored_up_std_factor = up_std . groupby ( "date" ) . transform (
lambda x : zscore ( x , nan_policy = "omit" )
)
z_scored_wr_down = wr_down . groupby ( "date" ) . transform (
lambda x : zscore ( x , nan_policy = "omit" )
)
return z_scored_up_std_factor + z_scored_wr_down
start = datetime . date ( 2009 , 1 , 1 )
end = datetime . date ( 2020 , 4 , 30 )
barss = load_bars ( start , end , universe = 50 )
factor = calc_ubl_factor ( barss , 20 )
ms = Moonshot ()
ms . backtest ( factor , barss )
ms . plot_cumulative_returns_by_quantiles ()
将代码中的universe = 50改为 3000,我们得到的分组结果也差不多。
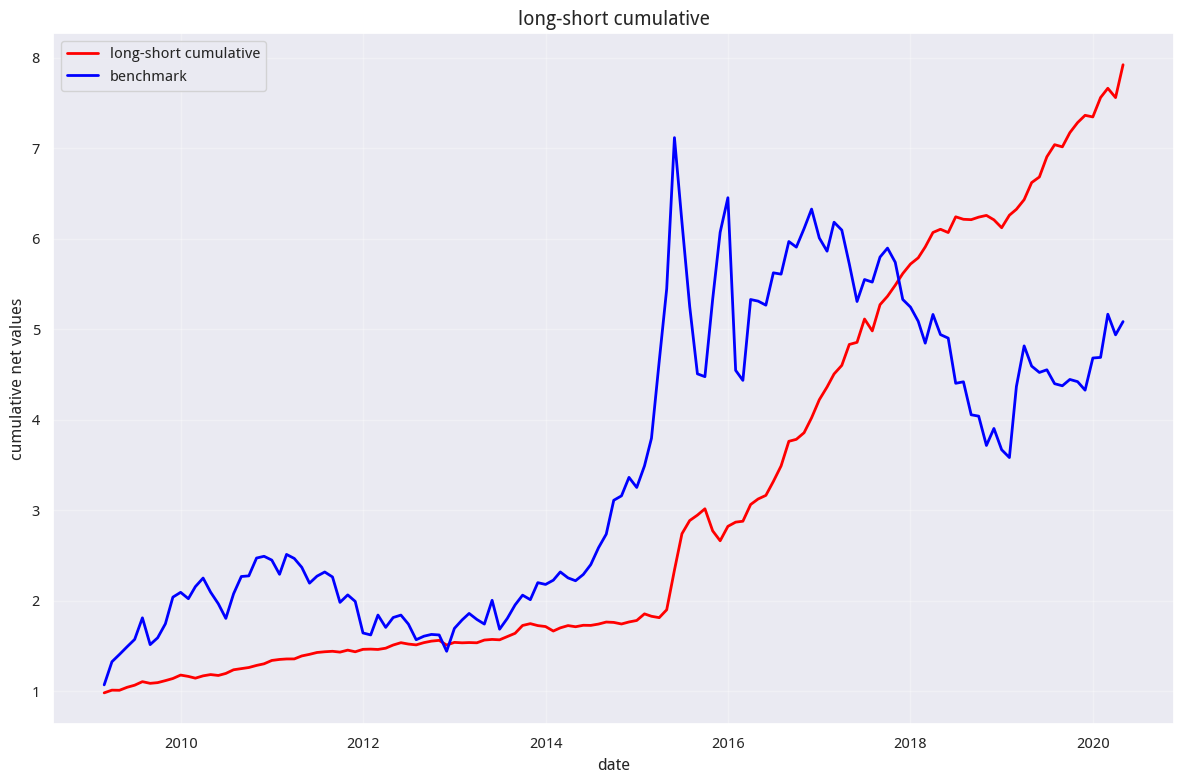
从分层累计收益上看,似乎跟单个因子(即单独的蜡烛上影线标准差或者单的威廉下影线均值)差不多。不过关键在于,此时的多空组合表现出非常稳健的特性:
在投资中,比起鳞鳞远峰见 ,我们更喜欢淡淡平湖春 。我们热爱这些 45 度仰望星空的净值曲线。
研报只回测到 2020 年 4 月。后来的情况怎么样? 你可以在 Quantide Research Platform 上阅读此文的 notebook 版本,改一下参数,自己跑跑看,应该有惊喜。
最后一段:关于截面 zscore 的思考
按照研报,在计算 ubl 因子时,应该在求得 up_shadow_std 因子和 wr_down_mean 因子之后,按日对它们进行截面 zscore 处理。我们在例子中,实现了这个要求。
但是,这真是必要的吗?
首先我们要注意,zscore 的默认值,具有 nan 传染性。也就是说,如果在某天的输入因子中,只要有一支资产的因子值是 nan,就会导致该日所有资产 zscore 化的计算值都是 nan,这样会导致此后的计算全无意义。
因此,如果必须要使用zscore,我们也一定要处理好这种情况。这是为什么在上面的例子中,我们在 transform 中,要传入lambda x: zscore(x, nan_policy='omit')的原因。
第二,我们对因子 zscore 化,并不会改变同一日因子之间的排序。而在此后进行因子分组收益计算时,正是按排序进行的分组。所以,这里进行截面 zscore 化,可能只是一种习惯,至少对分组累计收益的计算是没有影响的。