papers »
『匡醍译研报 01』 驯龙高手,从股谚到量化因子的工程化落地
头上三柱香,不死也赔光。这是一句股谚,说得是如果在高位出现三根长上影线,那么股价短期内很可能会下跌。因为上影线代表了上面的抛压特别大。这种说法能得到统计数据上的验证吗?来自东吴证券的一份研报,就讨论了这个问题。
这份研报给出一个很价值的结论,那就是,影线好不好用,关键点不在影线本身,而在于你如何使用它。这份研报从常见的 K 线形态出发,联系到 Williams R 指标,并运用基础统计理论进行建模和拓展,无论是其结论,还是研究方法,对我们量化人来说都有很好的借鉴意义。
因子原理
影线本质上是当日股价在冲击最高价(或者最低价)失败的痕迹。最高价与最低价是当日资金多空博弈的结果,代表了市场认可的真实压力与支撑。这个观点在光大证券的研报(RSRS 因子那篇)中也有提到,是坊间普遍认可的一种观点。大家从不同的角度出发,使用不同的建模方法,就得到了精彩各异的因子。
这篇研报从传统上下影线的定义出发,在比较了威廉指标之后,创造性地把威廉指标也看作一种『影线』,然后分别使用均值归一化手法来处理原始影线(包括传统影线与威廉影线),再通过滑动平均与滑动标准差构造出 4 个因子,分别进行了因子测试。
在因子测试之后,他们发现标准化蜡烛上影线与均值化威廉下影线的选股能力较强,于是又将这两个因子组合成一个新的因子,即 UBL。
最终,他们得到的回测结果(2009 年到 2020 年 4 月 30 日)如下:
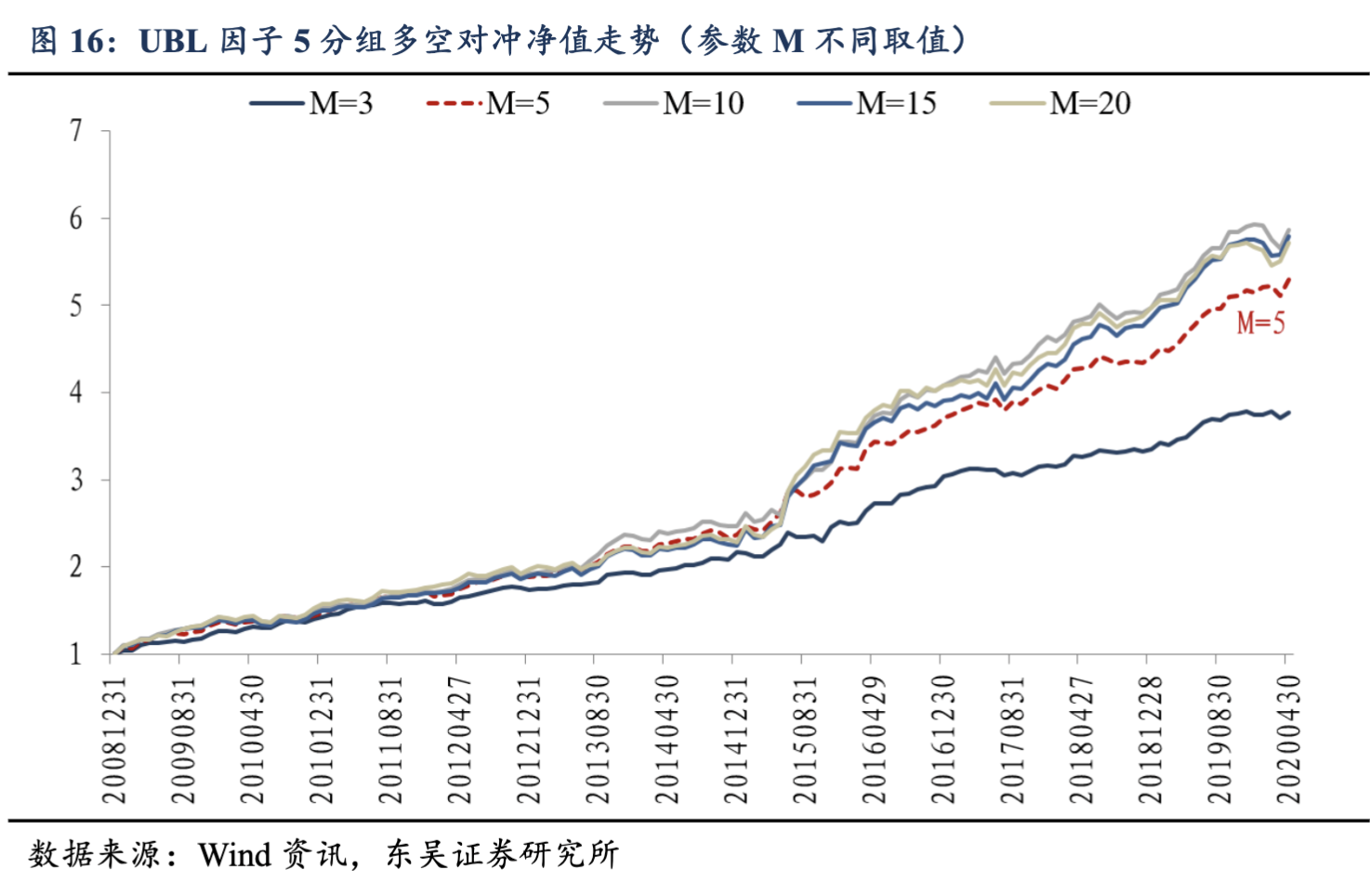
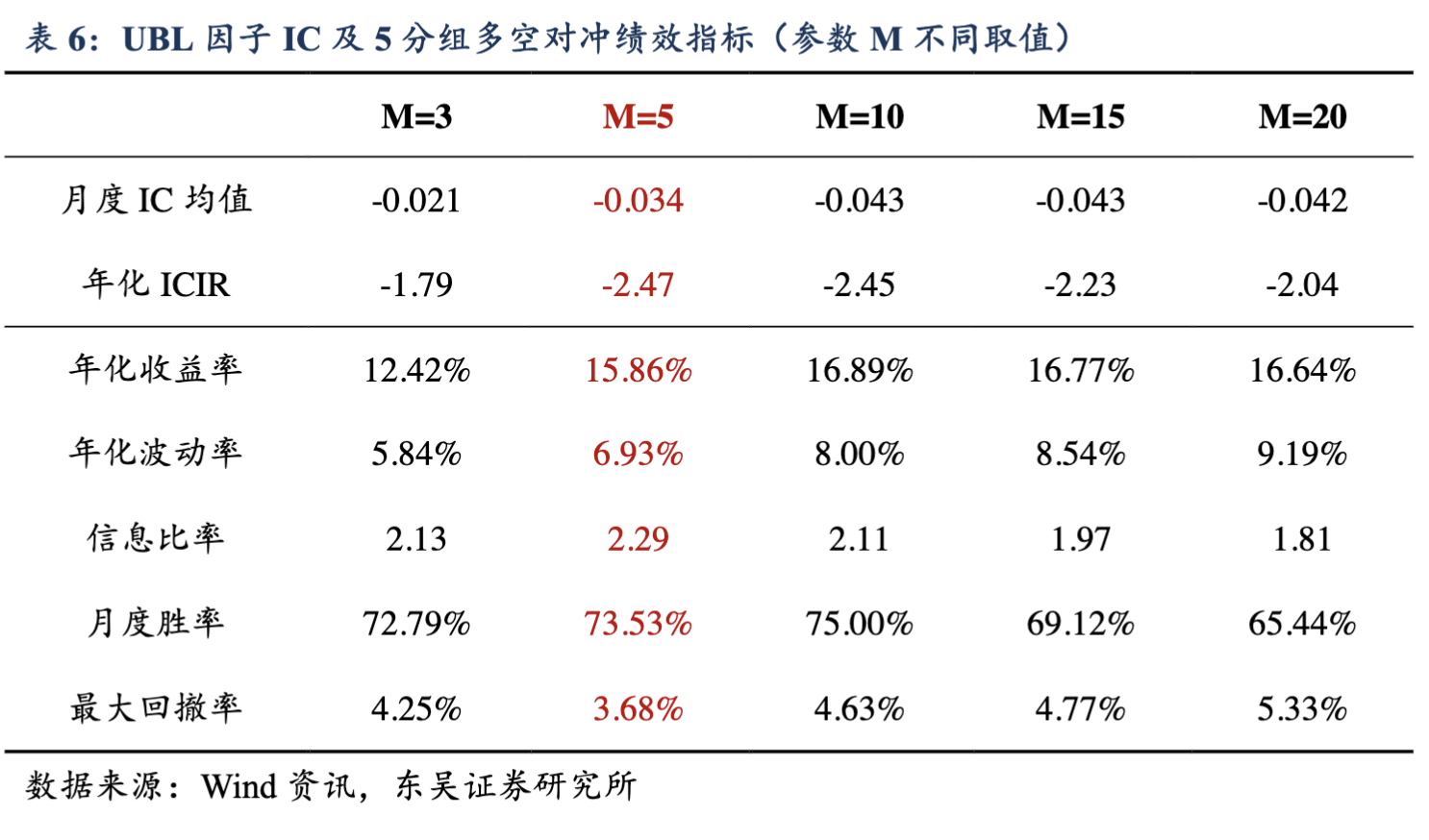
下面,我们就来实现这个因子。
因子构建
根据研报,因子的构建流程如下:

我们按图索骥,先来实现上下影线。
Tip
UBL 因子实现过程比较简单,非常适合初学者用来熟悉将研报『翻译』成为代码的过程。
上下影线
以下是计算上下影线的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | def calculate_shadow_ratio(bars):
"""计算上下影线因子(归一化)
按研报要求,标准化蜡烛上影线为当日上影线/过去 5 日上影线均值。标准化蜡烛下影线同。
"""
high = bars['high']
low = bars['low']
open_price = bars['open']
close = bars['close']
# 为避免除零错误,这里我们使用了一个技巧,即通过 mask 来排除可能除零的计算
# 无法计算时,设置为 0,表明无信号
up_shadow_ratio = pd.Series(0, index=bars.index)
down_shadow_ratio = pd.Series(0, index=bars.index)
up_shadow = high - np.maximum(open_price, close)
rolling_up_shadow = up_shadow.rolling(5).mean()
mask = rolling_up_shadow > 1e-8
up_shadow_ratio[mask] = up_shadow[mask] / rolling_up_shadow[mask]
down_shadow = np.minimum(open_price, close) - low
rolling_down_shadow = down_shadow.rolling(5).mean()
mask = rolling_down_shadow > 1e-8
down_shadow_ratio[mask] = down_shadow[mask] / rolling_down_shadow[mask]
return up_shadow_ratio, down_shadow_ratio
|
计算上下影线就是一句话的事儿。不过,按照研报要求,重要的是对它进行『标准化』:通过除以 5 日内影线的均值,以去掉不同资产之间的量纲差异。
从计算公式来看,我们必然面临一个除零的问题 -- 如果过去 5 天,该个股一直没有任何影线,那么,影线的 5 日均值就会是零。此时我们要如何避免除零的问题呢?
除零问题在量化建模时经常遇到,不同的场景下,解决方案都不一样。这里我们用了一点小技巧,值得一提。
Tip
代码中使用 rolling(5) 会导致前几期数据为 nan。此外,在收一字的情况下,上下影线不存在,还会产生除零的情况。我们必须通过 mask 把它们从计算中排除掉。
关键是如何将它们找补回来?对上下影线,这里我们设置的是零,表明无信号:既然没有影线存在,当然也就不存在影线的信号,因此这是合适的。
戏法人人会变,各有巧妙不同。在这些地方,每个人工程化的考量可能会有不同,也导致最终结果的差异。
威廉指标变种
研报作者认为,威廉指标的变种,即当日收盘价与最高价、最低价的差值(标准化后),也反映了卖压和买气,因此具有信号意义。
它的计算方法是:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | def calculate_williams_r_ratio(bars):
"""
计算变种威廉指标
"""
high = bars['high']
low = bars['low']
close = bars['close']
wr_up = high - close
wr_down = close - low
rolling_wr_up = wr_up.rolling(5).mean()
rolling_wr_down = wr_down.rolling(5).mean()
# 与蜡烛上下影线的默认值不同,0.5 更能表明无信号的含义
wr_up_ratio = pd.Series(0.5, index=bars.index)
wr_down_ratio = pd.Series(0.5, index=bars.index)
mask = rolling_wr_up > 1e-8
wr_up_ratio[mask] = wr_up[mask] / rolling_wr_up[mask]
mask = rolling_wr_down > 1e-8
wr_down_ratio[mask] = wr_down[mask] / rolling_wr_down[mask]
return wr_up_ratio, wr_down_ratio
|
月度因子计算
研报在因子上做了多重变换。到目前为止,我们还仅仅是进行了第一重变换:『标准化』。但真正的因子是在每个月末时计算出的均值或者标准差。
这部分操作有通用性,我们将它提取为一个函数。这当中运用了不少 pandas 的操作技巧。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | def calc_monthly(daily_factor, aggfunc, win=20):
dates = daily_factor.index.get_level_values('date').unique().sort_values()
month_ends = dates.to_frame(name = "date").resample('BME').last().values
dfs = []
for date in month_ends:
date_ts = pd.Timestamp(date.item())
iend = dates.get_loc(date_ts)
istart = max(0, iend - win + 1)
start_ = pd.Timestamp(dates[istart])
end_ = date_ts
window_data = daily_factor.loc[start_: end_]
df = (window_data.groupby(level="asset")
.agg(aggfunc)
.to_frame("factor")
)
df["date"] = date_ts
dfs.append(df)
df = pd.concat(dfs)
return df.set_index(["date", df.index]).sort_index()
|
在这一步中,我们实现了在每个月末,以 win 为数据窗口,计算一次月度因子。研报中,使用的均值和标准差都是一种聚合函数,为了允许探索更多的因子,我们在这里允许把聚合函数作为参数传入。
有了这个函数,我们就可以立即计算出研报开头提出来的蜡烛上_mean, 蜡烛上_std 等因子:
| def calc_candle_up_std_factor(barss, win = 20):
up_shadow = (barss.groupby("asset", group_keys=False)
.apply(lambda x: calculate_shadow_ratio(x)[0])
.sort_index())
return calc_monthly(up_shadow, "std", win)
|
现在我们得到的因子数据大致是:
同样,我们可以计算出威廉下_mean 因子:
| def calc_wr_down_factor(barss, win = 20):
wr_down = (barss.groupby("asset", group_keys=False)
.apply(lambda x: calculate_williams_r_ratio(x)[1])
.sort_index())
return calc_monthly(wr_down, "mean", win)
|
UBL 因子
根据研报,计算 UBL 因子需要在上述月度因子的基础上,进行市值中性化,再将两个因子,分别按横截面进行标准化,再求和。
这里我们省略掉市值中性化的步骤,直接进行截面 zscore 化。
Tip
『翻译』这篇研报的关键是,掌握滑动窗口下的均值、标准差、中性化和截面 zscore 等常用因子构造方法的程序化。从编程技巧上看,要重点掌握 rolling, groupby, transform, apply, lambda 以及多重索引操作等。
| def calc_ubl_factor(barss, win = 20):
from scipy.stats import zscore
up_std = calc_candle_up_std_factor(barss, win)
wr_down = calc_wr_down_factor(barss, win)
# 截面 zscore
z_scored_up_std_factor = up_std.groupby("date").transform(zscore)
z_scored_wr_down = wr_down.groupby("date").transform(zscore)
return z_scored_up_std_factor + z_scored_wr_down
|
我们可以通过以下数据来检验因子计算过程的正确性。
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | dates = pd.bdate_range('2019-01-01', '2019-01-31')
cols = ["open", "high", "low", "close"]
df1 = pd.DataFrame([(2, 3, 1, 2)] * len(dates), index=dates, columns=cols)
df1["asset"] = "A"
df2 = pd.DataFrame([(2, 3, 0, 0)] * len(dates), index=dates, columns=cols)
df2["asset"] = "B"
barss = pd.concat([df1, df2]).set_index("asset", append=True)
barss.index.set_names(["date", "asset"], inplace=True)
barss.sort_index(inplace=True)
display(calc_candle_up_std_factor(barss, 20))
display(calc_wr_down_factor(barss, 20))
|
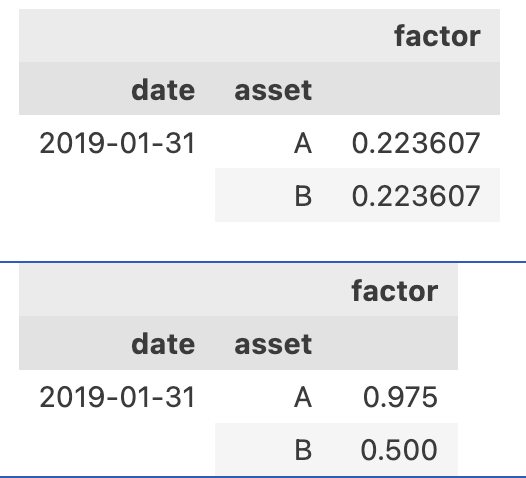
我们得到的上影线标准差因子,资产 A 与 B 都是 0.22367。
为简单起见,我们的测试数据中资产的上影线都设置成了相同的值。为何标准差并不为零呢?这是因为在计算过程中,前几个交易日由于滑动窗口 (win=5) 不足,产生了缺失值,这些缺失值被我们填充为零。这些零值与后续的非零值一起计算,导致了标准差为 0.22367。
Tip
如果你通过np.std来计算[0, 1, ..., 1] (共19个1),你会得到0.2179,而不是我们这里给出的0.2237。这是由于numpy与pandas在计算标准差时,默认的自由度不同导致的。具体来说,pandas.Series.std()默认使用ddof=1(样本标准差),而numpy.std()默认使用ddof=0(总体标准差)。在量化因子构建中,这种细微差异可能会影响因子的表现。
对威廉下影线_mean 因子,结果更容易理解一些。在 20 个交易日里,第一个标准威廉下影线是缺失值,被我们替换成了 0.5,因此,结果中的 0.975 就是数组 0.5, 1, ..., 1的均值;对资产 B,由于它的下影线一直是 0,所以,全部被换成了 0.5,因此均值也就是 0.5。
结论
这篇文章我们拿了一个非常简单的例子,来讲解如何读研报、将研报翻译成代码。在了解基本的术语(比如均值、标准差、截面标准差、zscore)之后,剩下的就是要注意一些工程实践中的细节,比如如何处理缺失值,给它们赋予恰当的默认值。这部分往往在研报中讲的比较少,它常常来自于你的交易经验、来自于你对因子的理解。
此外,本文也提到了不同的 Python 库在一些基本概念实现上的不同,比如大家耳熟能详的标准差计算,Pandas 与 Numpy 就有不同。通常情况下(只把标准差当成衡量误差的尺度时),这种差异可以忽略,但一旦我们将它用作因子,你可能注要注意这种差异了。
量化不只是有一个 idea,就能自动付诸实施。量化交易策略的成功,既需要我们『天才』般的创意与创新,也需要我们能够深入每一个细节,正确实现它。这往往需要经过系统的训练。匡醍的量化课程以其严谨、体系化的课程内容著称,如果你正在寻找这样一门课程,强烈推荐你学习匡醍的『量化二十四课』和『因子挖掘与机器学习策略』课程。
本文为系列文章,下一篇我们将进行因子回测,来验证研报的结论。欢迎关注订阅,及时得到更新。本文(及后续文章)附有源代码,可在 Quantide Research 平台阅读和运行。