papers »
RSRS 择时指标
Table of Content
RSRS 因子在 2005 年 3 月到 2017 年 3 月的上证 50 指数上,12 年总收益 1432.36% ,年化 24.84% ,夏普 1.42。同期指数收益仅为 290.13%。
该指标的大致思想是,将每日最高价与最低价分别视为阻力位与支撑位,把给定周期下线性回归拟合得到的斜率作为因子。斜率越陡,表示市场强度越强。
本文复现了 RSRS 因子,可运行的完整代码和数据在我们的研究平台中提供。如果你关心它的最新表现,或者任何一段时间的表现,只需要自己修改时间参数运行即可得到答案。
RSRS(Resistance Support Relative Strength) 因子是光大证券于 2017 年起的系列中,提出的一种择时因子。该系列最初发表于 2017 年,后来又在 2019 年和 2021 年对之前的因子构造进行了回顾和优化。这篇 notebook 将复现这一因子,并对其构造思想进行解读。
这是我们系列研报解读中的一篇。持续跟踪本系列文章,你将掌握复现研报所需要的理论知识、编程技巧、数据获取方案和交易策略经验,换言之,成为一名熟练的策略研究员。
在解读每一篇研报时,我们都会选附上研报原文:
然后才是我们对研报的解读和复现:
通过对比,你可以发现我们对研报进行了提炼和挖掘,主题思想更明确,也更容易读懂。
该策略的主要思想是:
Tip
最高价与最低价当日市场全体参与者博弈出来的真实阻力与支撑。
在相邻的两个时间点 [T0, T1] 之间,最高价 High 的变化值 \(\Delta_H = High(T1) - High(T0)\) 和最低价 Low 的变化值 \(\Delta_L = Low(T1) - Low(T0)\) ,两者的比值反应了阻力位与支撑位的相对强度,即 RSRS 指标。
为了过滤噪声,一般取\(T_1, T_2, ...T_n\) 间的最高价和最低价进行线性回归,此时得到的斜率\(\beta\) 即为 RSRS 指标,在本质上与定义 2 相同,即有以下公式:
\[
high = alpha + beta * low + epsilon, epsilon ~ N(0, sigma)
\]
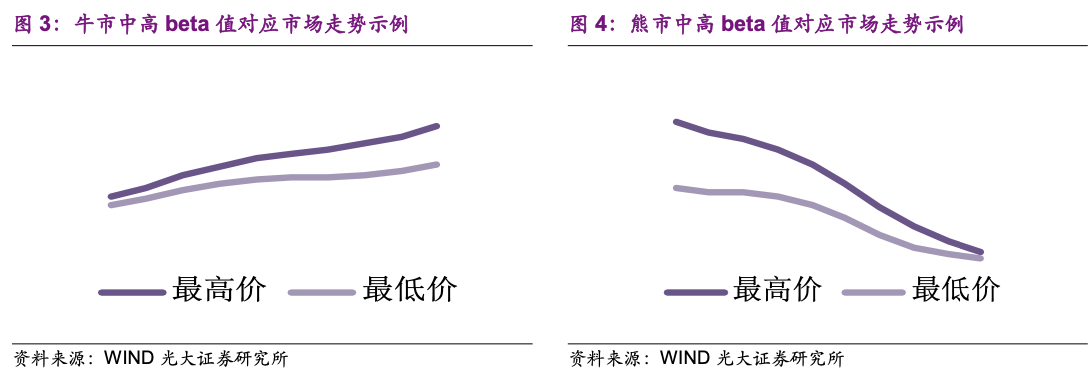
应该说策略的思想非常巧妙,也很符合我们的交易认知:如果市场投资者认为下面的支撑很强,就敢于向上试探更大的空间,因此最高价的涨幅就变大;如果市场投资者认为上方的压力很大,则更期望尽快脱手,从而导致最低价格的跌幅变大 。
研报作者还手绘了两幅图来说明这一思想:
研报还展示了如何为交易思想建模的一个简单但常用的技巧,即线性回归。线性回归是从简。丁伯格等人开创计量经济学以来,在经济和金融领域广泛使用的一种技巧。在这里,线性回归的引入,让交易思想得到合理的抽象,成为有统计实证支持的一个模型。
这个因子的计算方法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14 import pandas as pd
def calc_rsrs_factor ( df : pd . DataFrame , win : int = 18 ):
df = df . copy ()
# 计算滑动窗口的协方差 Cov(low, high)
rolling_cov = df [ "low" ] . rolling ( window = win ) . cov ( df [ "high" ])
# 计算滑动窗口的方差 Var(low)
rolling_var = df [ "low" ] . rolling ( window = win ) . var ()
df [ "RSRS" ] = rolling_cov / rolling_var
return df [ "RSRS" ]
Tip
在这里我们使用了一个快速的向量化算法。如果你感到难以理解这个算法,那么,它对应的 vanilla 版本是这样:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 def calc_rsrs_vanilla ( df , N ):
df = df . copy ()
temp = [ np . nan ] * N
for row in range ( len ( df ) - N ):
y = df [ 'high' ][ row : row + N ]
x = df [ 'low' ][ row : row + N ]
# 确保 x 和 y 的长度都为 N,并且没有 NaN 值
if len ( x ) == N and len ( y ) == N and not x . isnull () . any () and not y . isnull () . any ():
beta = np . polyfit ( x , y , 1 )[ 0 ]
temp . append ( beta )
else :
temp . append ( np . nan )
df [ 'rsrs' ] = temp
return df
在对比测试中,vanilla 版本的运行时间如果是 4.3ms 的话,那么向量化版本的运行时间则仅为 317us,快了 10 倍多。
现在,我们通过 tushare 的数据,来看一下因子计算的结果。下面的代码展示了如何获取 hs300 指数数据:
hs300 = pro . index_daily ( ts_code = "000300.SH" , start_date = "20250101" , end_date = "20250601" )
hs300 . index = pd . to_datetime ( hs300 [ "trade_date" ])
hs300 = hs300 . sort_index ( ascending = True )
Tip
在使用 tushare 的行情数据时,请务必按照这里的代码片段,先将 trade_date 设置为索引,然后进行排序,这样得到的数据的顺序,才会与大多数软件系统中的顺序一致。
现在,我们就可以计算出 RSRS 因子了:
hs300_factor = calc_rsrs_factor ( hs300 , 18 )
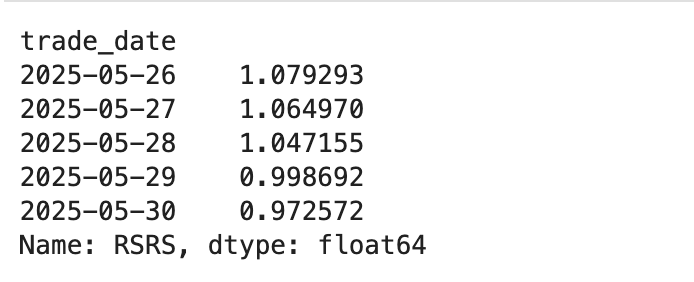
hs300_factor
我们看到,hs300_factor 是一个 pd.Series,它的索引是日期,其值是因子值。这样的格式有利于后面合并横截面数据。
因子的质量如何?我们可以使用 Alphalens 来进行检验。Alphalens 是一个用于评估因子的库,简单易用,非常适合对因子进行快速评估。不过,它主要采用的是横截面评估法,因此,我们需要先获取沪深 300 指数中,所有成份股的历史数据,再计算出它们的因子值。
Tip
看了很多研报,但却不知道如何复现?2025 年,你应该加入匡醍研究平台,手把手带你复现研报。全年仅 360 元,即可享有超 100 份研报、复现代码及运行环境!在该运行环境中,提供了 Tushare 高级账户使用权(官方价格 500 元),仅此一项,就值回票价!
在我们的研究环境中,有从 2005 年到 2023 年所有个股的日线历史数据,可以允许我们进行较长周期的因子测试,并且已经有封装好的 alpha_test 方法可以调用。不过,我们还需要先获取沪深 300 成分股列表。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 df = pro . index_weight (
index_code = '000300.SH' ,
start_date = '20231201' ,
end_date = '20231231'
)
# 在研究环境中,我们使用的股票代码是以。XSHG 或者。XSHE 结尾的,所以,我们需要将股票代码转换一下。
def convert_symbol ( x : str ):
if x . endswith ( ".SH" ):
return x . replace ( ".SH" , ".XSHG" )
elif x . endswith ( ".SZ" ):
return x . replace ( ".SZ" , ".XSHE" )
else :
raise ValueError ( f " { x } : not supported format" )
universe = tuple ( map ( convert_symbol , df [ "con_code" ] . unique ()))
universe [: 5 ]
现在,我们就调用 alphatest 来进行因子测试:
start = datetime . date ( 2018 , 1 , 1 )
end = datetime . date ( 2021 , 12 , 31 )
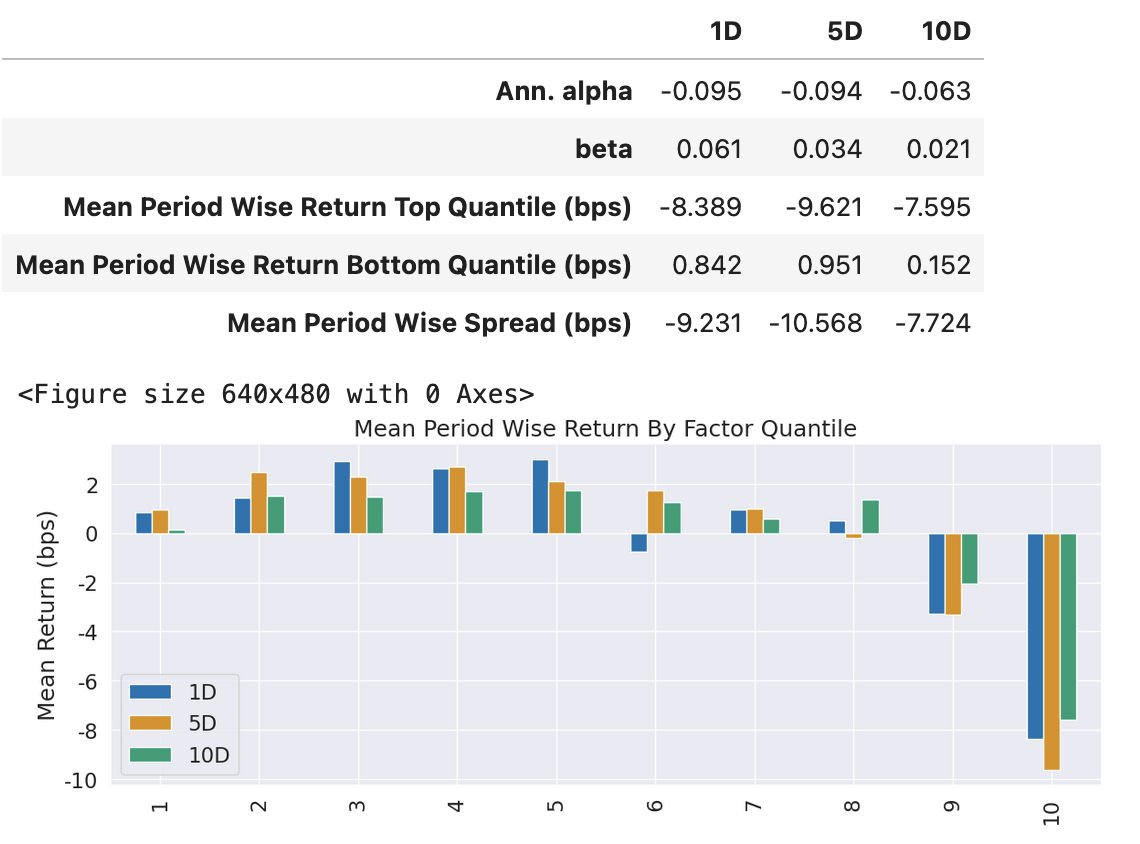
_ = alphatest ( universe , start , end , calc_rsrs_factor )
输出结果有点小意外,没有出现你期待的高收益,基至年化 Alpha 还是负的。不过,对 Alphalens 的输出我们需要辩证来看,这个简单的测试,已经说明了这个因子很可能是有 Alpha 存在的(它的 beta 接近于零),只是年化为负,这种情况下,我们只要修改因子的方向,即可得到正的年化收益。
不过,Alphatest 的结果与研报相去甚远,这应该作何解释呢?
原来,研报中 RSRS 指标的交易方式阈值买入卖出式。它要求先对过去 M 个交易日的斜率因子进行分层统计,取均值±一个标准差的值作为买入和卖出的阈值,所以,这是一种事件型交易方式,使用 Alphalens 就无法准确地回测出它的收益率。
Tip
Alphalens 默认的回测方式是横截面式的。尽管后期也加入了事件型回测,但支持的并不完善。也可能是考虑回测框架已经有了完善的事件回测机制,所以就没在这方面多下功夫?随着 Quantopian 的解散,今天我们已无从得知其中的缘由。
这里的 alphatest 是我们在《因子分析与机器学习策略》课程中开发的一个辅助函数,它在底层调用了 alphalens 的回测函数,但进行了一些简化,使得我们可以仅仅通过一行代码,就完成因子回测。
另一个区别是,研报使用交易标的是沪深 300 指数,它是由各个标的按一定权重构建出来的价格序列;当我们使用 alphalens 进行回测时,我们相当于构建了一个等权沪深 300 指数。这两个指数之间本来就会有差异。
现在,我们就回到研报的实现,对沪深 300 指数本身进行交易回测。
事件型交易策略必须要能给出交易信号。根据前面的叙述,这个交易信号是均值的一个标准差。为此,我们需要先对过去 M 天的 RSRS 进行统计,并计算出均值和标准差,然后进行 zscore 化。
不过,在开始之前,我们先对因子进行可视化,找一点点感觉。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as st
def describe ( df , col , title ):
data = df [ ~ df [ col ] . isna ()][ col ]
# 创建图形
fig , axes = plt . subplots ( 1 , 2 , figsize = ( 18 , 9 ))
plt . suptitle ( title )
# 基本统计量
avg = data . mean ()
std = data . std ()
# 左侧:直方图
sns . histplot ( data , kde = False , stat = 'density' , alpha = 0.4 , ax = axes [ 0 ])
for line , color , label in zip (
[ avg , avg - std , avg + std ],
[ 'red' , 'blue' , 'blue' ],
[ 'Mean' , '-1 Standard Deviation' , '1 Standard Deviation' ]
):
axes [ 0 ] . axvline ( x = line , color = color , linestyle = '--' , linewidth = 0.8 , label = label )
axes [ 0 ] . set_ylabel ( 'Percentage' , fontsize = 10 )
axes [ 0 ] . legend ( fontsize = 12 )
# 右侧:KDE 和正态分布拟合
x = np . linspace ( avg - 3 * std , avg + 3 * std , 100 )
kde = st . gaussian_kde ( data )
y_norm = st . norm . pdf ( x , avg , std )
axes [ 1 ] . plot ( x , kde ( x ), label = 'Kernel Density Estimation' )
axes [ 1 ] . plot ( x , y_norm , color = 'black' , linewidth = 1 , label = 'Normal Fit' )
axes [ 1 ] . axvline ( x = avg , color = 'red' , linestyle = '--' , linewidth = 0.8 , label = 'Mean' )
axes [ 1 ] . set_ylabel ( 'Probability' , fontsize = 10 )
axes [ 1 ] . legend ( fontsize = 12 )
return plt . show ()
# 调用函数
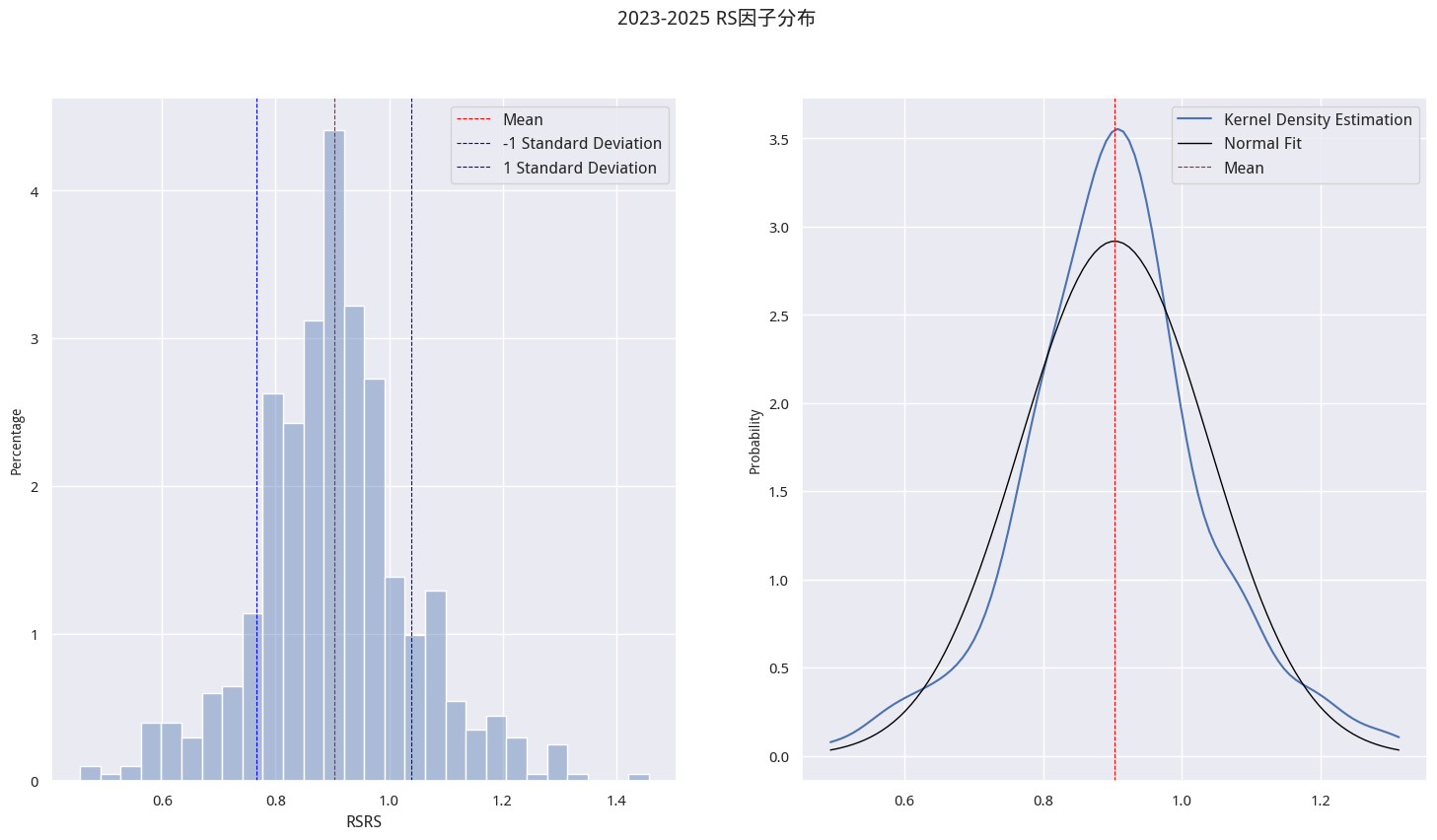
describe ( hs300_factor . to_frame (), 'RSRS' , '2018-2025 斜率数据分布' )
斜率数据分布
根据研报和运行结果,卖出阈值在 0.8 附近,买入阈值在 1.0 附近。即如果 RSRS 指标大于 1.0,买入并持有;当 RSRS 回落到小于 0.8 时,就卖出。
如果我们以此确定阈值,就会犯了前视偏差的错误:我们把 2023 到 2025 的全部数据纳入了统计,但如果交易发生在 2023 年底呢?除非这些年来,RSRS 的分布一直保持不变,否则,我们就一定是参考了错误的阈值。
因此,我们需要以滑动窗口来确定交易阈值,即在\(T_0 ~ T_m\) 个交易日中,找到 25%和 75%分位值,分别作为第 m 日买入或者卖出的阈值。在研报中,它换了另一种方式:将 high 对 low 的 N 日回归斜率,按 win 个窗口进行 z-score 化。在 z-score 化之后,如果当日因子值大于 0.7,则认为此处为买入信号;如果当日因子值小于-0.7,则认为此处为卖出信号。
Info
在标准正态分布中,数值 0.7 对应的分位数是 75.8%,负 0.7 对应的分位数是 24.9%。研报在这里没有严格遵循之前讲的±1 个标准差,可能是为了与 25%,75%这样的常用分位数对齐。
现在,我们按研报思想,对原始的 RSRS 因子进行滑动窗口处理。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 start = "20180101"
end = "20250601"
hs300 = pro . index_daily ( ts_code = "000300.SH" , start_date = start , end_date = end )
hs300 . index = pd . to_datetime ( hs300 [ "trade_date" ])
hs300 = hs300 . sort_index ( ascending = True )
def calc_rsrs ( df : pd . DataFrame , win : int = 18 ):
df = df . copy ()
# 计算滑动窗口的协方差 Cov(low, high)
rolling_cov = df [ "low" ] . rolling ( window = win ) . cov ( df [ "high" ])
# 计算滑动窗口的方差 Var(low)
rolling_var = df [ "low" ] . rolling ( window = win ) . var ()
df [ "rsrs" ] = rolling_cov / rolling_var
return df
def calc_rsrs_zscored ( df : pd . DataFrame , n : int = 18 , m : int = 600 ):
df = calc_rsrs ( df , n )
df [ "rsrs_" ] = df [ "rsrs" ] . fillna ( 0 )
ZSCORE = ( df [ 'rsrs_' ] - df [ 'rsrs_' ] . rolling ( m ) . mean ()) / df [ 'rsrs_' ] . rolling ( m ) . std ()
df [ 'rsrs_z' ] = ZSCORE
return df . drop ( columns = 'rsrs_' )
rsrs_z = calc_rsrs_zscored ( hs300 , 18 , 600 )
我们可以观察下 z-score 化后的因子:
describe ( rsrs_z , 'rsrs_z' , '2018-2025 Z-Score 化后的 RSRS 分布' )
结果与前图(斜率数据分布)差别不大,此处从略。
现在我们来构建一个简单的交易策略:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63 import matplotlib.dates as mdate
def RSRS_Strategy ( start : datetime . date , end : datetime . date , n : int = 18 , m : int = 600 ):
start_ = start . strftime ( "%Y%m %d " )
end_ = end . strftime ( "%Y%m %d " )
data = pro . index_daily ( ts_code = "000300.SH" , start_date = start_ , end_date = end_ )
data . index = pd . to_datetime ( data [ "trade_date" ])
df = data . sort_index ( ascending = True )
rsrs_z = calc_rsrs_zscored ( df , n , m ) # 计算标准分指标
# 需要扣除前期计算的 600 日
rsrs_z = rsrs_z [ max ( n , m ):]
print ( '回测起始日:' , min ( rsrs_z . index ))
z_singal = []
threshold = 0.7
for row in range ( len ( rsrs_z )):
if rsrs_z [ 'rsrs_z' ][ row ] > threshold :
z_singal . append ( 1 )
else :
if row != 0 :
if z_singal [ - 1 ] and rsrs_z [ 'rsrs_z' ][ row ] > - threshold :
z_singal . append ( 1 )
else :
z_singal . append ( 0 )
else :
z_singal . append ( 0 )
# 交易信号
rsrs_z [ 'z_singal' ] = z_singal
# 每日收益
rsrs_z [ 'ret' ] = rsrs_z [ 'close' ] . pct_change ()
# 累积净值
z_cum = ( 1 + rsrs_z [ 'z_singal' ] * rsrs_z [ 'ret' ]) . cumprod ()
# 基准净值
benchmark = ( 1 + rsrs_z [ 'ret' ]) . cumprod ()
# 画图
plt . figure ()
fig = plt . figure ( figsize = ( 20 , 10 ))
ax1 = fig . add_subplot ( 1 , 1 , 1 )
ax1 . plot ( z_cum , label = 'RSRS 策略' )
ax1 . plot ( benchmark , label = '沪深 300' )
ax1 . xaxis . set_major_formatter ( mdate . DateFormatter ( '%Y-%m' ))
plt . legend ( loc = 'best' )
plt . xlabel ( '时间' )
plt . ylabel ( '净值' )
plt . title ( 'RSRS 指标策略净值曲线' )
plt . show ()
return z_cum , benchmark
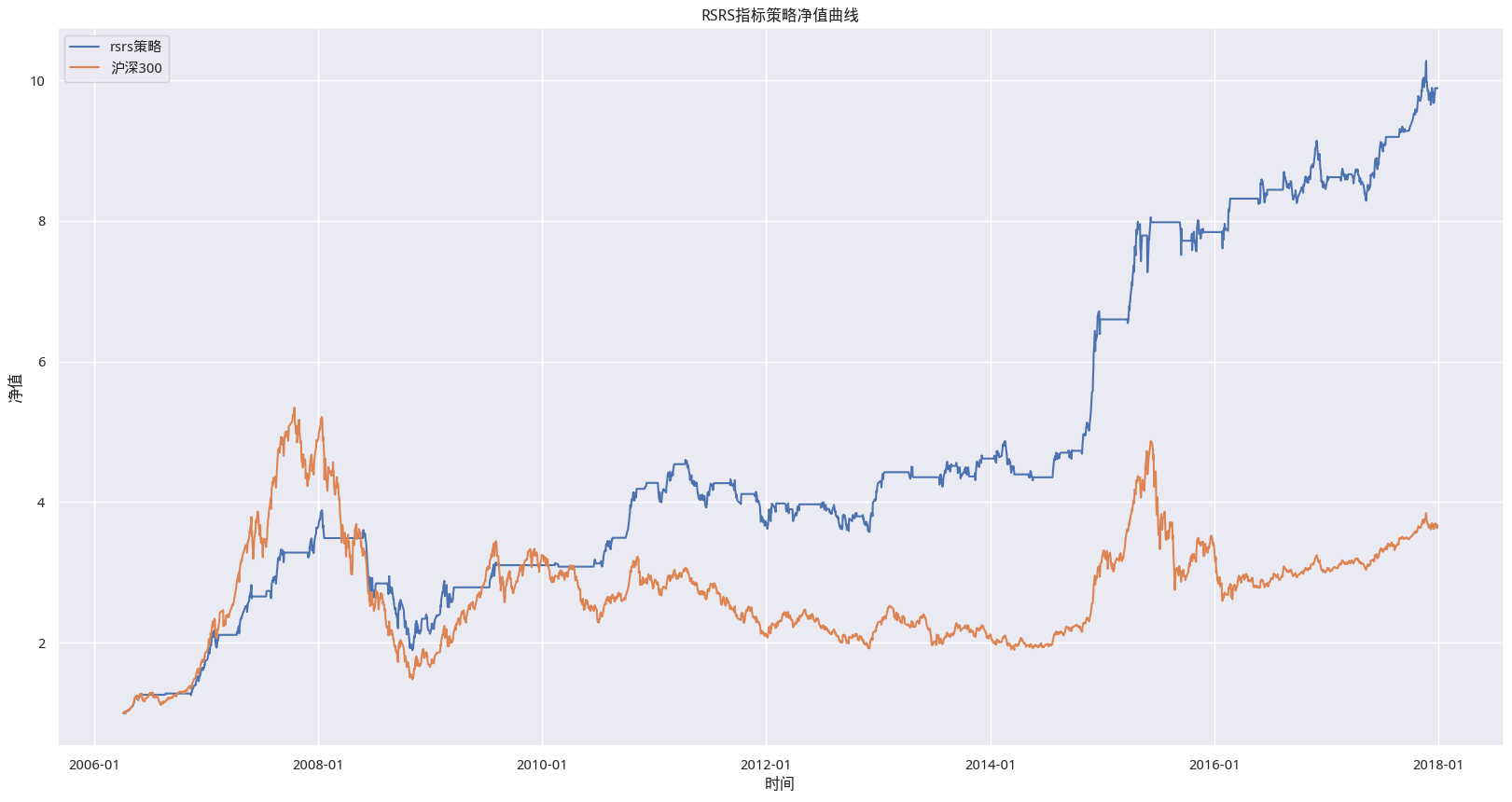
strategy , benchmark = RSRS_Strategy (
datetime . date ( 2005 , 1 , 1 ), datetime . date ( 2018 , 1 , 1 ), m = 300
)
研报发表于 2017 年,我们使用了 2005 年到 2018 年间共 11 年的数据进行了回测,从简单的净值曲线来看,策略以 10 倍的涨幅,远远超过了基准模型,与研报结果相接近。
本文部分代码参考了 Hugo2046 的 github 项目 ,特此鸣谢。
 斜率数据分布
斜率数据分布