others »

[1027] QuanTide Weekly

#others #weekly #factor

Table of Content

本周要闻¶

财政部：中国还将加大财政政策逆周期调节力度
统计局：1-9月全国规上工业利润下降3.5%
纽交所计划延长美股交易时间。

下周看点¶

周一：医保目录现场谈判开始
周四：统计局发布10月PMI
美股Q3财报季下周将迎来最繁忙的一周

本周精选¶

连载！量化人必会的 Numpy 编程(8) - 暴力美学，无洗盘，不拉升。洗盘模式如何检测？(应用案例5)

10月25日，世行举行发展委员会第110次会议。财政部副部长廖岷表示，中国还将加大财政政策逆周期调节力度，在化解地方政府债务、稳定房地产市场、提高重点群体收入、保障民生、推动设备更新和消费品以旧换新等方面实施一系列强有力措施。中国有信心实现5%增长目录（财政部网站）
1—9月份，全国规模以上工业企业实现利润总额52281.6亿元同比下降3.5%。
今日2024年医保目录现场谈判/竞价正式拉开帷幕，医保局工作人员现场点名华润医药、百特药业、康缘药业、康哲药业、宜昌人福、正大天晴等在内十余家多家企业先后进场，节奏明显快于去年。
北交所分别举办券商、上市公司两场专项座谈会，会议提出，北交所将推动提高企业运用并购重组工具的能力，促进提高北交所上市公司质量和投资价值
三季度中央汇金大举增持多只宽基ETF 仅4只沪深300ETF和华夏上证50ETF就耗资3000亿元
纽交所计划延长美股交易时间至每个工作日22小时。

来源：财联社网站

暴力美学!无洗盘，不拉升。洗盘模式如何检测？¶

无洗盘，不拉升。 筹码收集阶段，股价呈现出上涨形态，也吸引到许多不坚定的跟风盘，它们将成为主升过程中的不利因素。

因此，在拉升之前，主力会采用洗盘的方式，将这些不坚定的低价筹码洗下车。这个过程中往往暴涨暴跌，犹如一匹烈马，要摆脱它身上的骑手一样。

暴力洗盘，某种程度上就成为了行情快速上涨之前的信号之一。

这篇文章，我们量化实现的技术问题：如何快速检测出洗盘模式？

L50

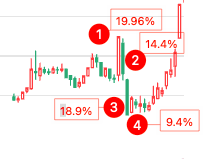
暴力洗盘是在证券市场上观察到的一种经验模式，因此没有严格的定义。一般把两阳夹一阴、且涨跌幅都巨大的情况认为是暴力洗盘。

在本文中我们把两阳夹两阴、且涨跌幅都较大的情况定义为暴力洗盘。

但我们介绍的方法，也完全适用于其它模式，只需要微调参数即可。

如左图所示，标的在1号位置之前，经过一段时间的吸筹，由于期间股价上涨，已经吸引了一些跟风盘。主力在1号位置拉出20cm，在这一过程中，较多跟风筹码被锁定在涨停位置。

第2天起主力开始洗盘，连续两天，分别下跌14.4%和18.9%。此时在1号位置买入的筹码因为忍受不住巨大的跌幅，忍痛交出筹码。主力筹码增加，成本降低，为后面的拉升留出了空间。

第4天主力将个股拉涨9.4%，表明洗盘结束。

随后几天的整理，主要是留出时间，让下一波的跟风盘有时间发现这支标的，并且有信心跟随买入。紧接着使用一系列小阳线做出上升趋势，最终再拉出一个20cm，从第4天起，短期涨幅高达87%。

我们为什么要使用两阳夹两阴的4天模式来定义洗盘？

因为经过两天的洗盘，从时间和空间上看，洗盘效果会更好（考虑到交易者心理因素，一些人第一天亏损后，往往还不会绝望，第二天继续下跌，更容易崩溃卖出）。另外，从一些技术指标上来看，经过连续两天大幅下跌，技术指标修复比较到位，也更能为后面的拉升腾出上涨空间。

我们为涨跌幅设置一个阈值，如果期间的每个bar的涨跌幅超过这个阈值，我们就认为发生了洗盘。在我们的示例中，使用的阈值是0.05，即涨跌5%。

下面我们来看代码实现：

# 示例1
def feature_washout(bars, threshold=0.05):
    """返回在bars中最后一次洗盘结束的位置，-1表示最后一个bar,
        0表示不存在洗盘模式
    """
    close = bars["close"]
    opn = bars["open"]
    truerange = np.maximum(np.abs(close[1:] - close[:-1]), 
                           np.abs(opn-close)[1:]) 
    # 百分比化
    tr = truerange / close[:-1]
    sign = (opn < close)[1:] * 2 - 1
    signed_tr = tr * sign

这里我们使用了truerange这个变量名,是因为这段代码脱胎于技术指标TR。

这段代码解决如何将涨跌幅转换为由1,-1和0表示的模式，以便我们后面进行模式检索。

如果当天涨跌超过5%，或者实体的振幅超过5%，我们就将其标记为1或者-1，否则标记为0。标记的符号由它的形态是阴线还是阳线决定。阴线为-1，阳线为1.

我们通过这样一段简单的代码就实现了求阴阳线的功能：

(opn < close) * 2 -1

¶

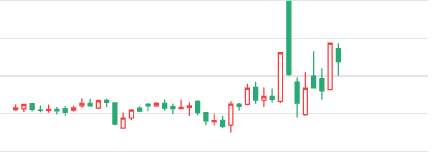
其结果将生成由1和-1组成的数组。无论是涨还是跌，我们总是认为，阴线是洗盘。所以，高开大阴线，即使收盘是上涨的，我们也当成洗盘来处理。

下图就是高开大阴线洗盘一例：

75%

在判断每个bar的涨跌幅、或者实体的振幅是否超过阈值时，我们使用了一个简单的技巧，即通过np.maximimum来从多个数组中，以 element-wise 的形式选取最大值。即，如果有数组\(A\)和\(B\)，那么\(np.maximum(A, B)\)将返回一个数组，其元素为\(A\)和\(B\)对应位置的元素中的较大值。

也就是，如果结果是\(C\)，那么\(C_0\)将是\(A_0\)和\(B_0\)中的较大值，\(C_1\)将是\(A_1\)和\(B_1\)中的较大值，以此类推。

除了使用\(np.maximimum\)这种 ufunc 之外，实际上\(np.max\)也可以用来完成这项任务，只是我们需要先将数组\(A\)和\(B\)堆叠成一个矩阵：

# 示例2
A = np.arange(4)
B = np.arange(3, 7)
C = np.arange(8, 4, -1)

Z = np.vstack((A,B,C))

# 通过np.max求每列最大值
r1 = np.max(Z, axis=0)

# 通过np.maximum求最大值
r2 = np.maximum.reduce([A, B, C])

# 比较两种方法的结果是否相同
np.array_equal(r1, r2)

为了提供更多信息，示例中我们演示了三个数组按元素求最大值的情况。答案是要使用reduce方法。如果只在两个数组间进行比较，则可以只使用np.maximum。

经过示例1处理后，我们可能得到如下所示的数组：

[ ... 0.04 -0.02 -0.06 0.04 -0.04 -0. 0.2 -0.14 -0.19 0.09 -0.03 ...]

显然，我们还应该把它二值化，转换成为[大阳,大阴,大阴,大阳]（即[1, -1, -1, 1]）这样的模式：

# 示例3
encoded = np.select([signed_tr > threshold, 
                    signed_tr < -threshold], 
                    [1, -1], 0)

for i in range(len(encoded) - 3, 0, -1):
    if np.array_equal([-1, -1, 1], encoded[i:i+3]):
        return i - len(encoded) + 2
return 0

我们通过select方法完成了二值化转换。接下来我们通过一个逆序的循环，通过array_equal完成了模式匹配。

在回测中，我们可能需要一次性地提取出很长一段行情中所有的洗盘模式，并对其效果进行检验。上面的代码还可以通过numpy.lib.stride_tricks.sliding_window_view进行优化：

def feature_washout(bars):
    ...
    washouts = []
    for i, patten in enumerate(sliding_window_view(encoded, window_shape = 4)):
        if np.array_equal(patten, [1, -1, -1, 1]):
            washouts.append(i)

    return washouts

通过将涨跌幅二值化，我们就可以在随后方便地通过array_equal来匹配模式。我们这样做，是因为在这里定性分析基本就够了，只要涨跌幅超过5%，那么无论是跌了5.1%还是7.2%，我们都认为是洗盘。

但是，如果你觉得定量分析仍然有意义，也可以通过求皮尔逊相关系数的方法来进行模式匹配。