others »

[0908] QuanTide Weekly

#others   #weekly   #numpy   #pandas  

---

Table of Content

本周要闻

• 央行：降准有空间 利率进一步下行面临一定约束
• 巴菲特再次减持美国银行，这次要做空自己的祖国？
• 存量房贷下调预期落空，沪指连续三日跌破2800点

下周看点

• 周一，8月CPI/PPI 数据发布
• 周一，茅台业绩说明会，对白酒行业的未来发展预判是重要信号

本周精选

• 那些必读的量化论文
• 连载！量化人必会的 Numpy 编程 (2)

---

本周要闻

• 央行货币政策司邹澜9月5日表示，是否降准降息还需观察经济走势。年初降准的政策效果还在持续显现，目前金融机构的平均法定存款准备金率大约为7%，还有一定的空间。同时，受银行存款向资管产品分流的速度、银行净息差收窄的幅度等因素影响，存贷款利率进一步下行面临一定的约束。
• 当地时间9月5日，美国证券交易委员会披露，巴菲特于9月4日前后连续三日减持美国银行套现约7.6亿美元。今年7月，他曾连续9天减持美国银行，在减持前，美国银行为其第二大重仓股，也是伯克希尔最赚钱的公司之一。
• 沪指本周下跌2.69%，连续三日跌破2800点。目前沪指PE值处在12%分位左右，属较低位置。消息面上，上周盛传的存量房贷降息预期落空。
• 证监会离职人员入股拟上市企业新规落地，要求更严、核查范围更广

消息来源：东方财富、财联社

---

那些必读的量化论文

1. Portfolio Selection, Markovitz, 1952。在这篇文章里，马科维茨提出了现代资产组合理论(MPT),使他获得了 1990 年诺贝尔经济学奖。该论文通过将风险与回报之间的相关性纳入计算中来扩展了常见的风险回报权衡。
2. A New Interpretation of Information Rate，Kelly, 1956。本文是当今著名的凯利准则的正式表述。该模型广泛应用于赌场游戏，特别是风险管理。作者推导出了一个公式，该公式确定了最佳分配规模，以便随着时间的推移最大化财富增长。
3. Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk (Sharpe, 1964)。基于Markovitz的工作，CAPM证明了只有一种有效的投资组合，即市场投资组合。这篇文章提出了著名的Beta概念。Sharpe和Markovitz是师生关系，同年获得诺贝尔经济学奖。
4. Efficient Capital Markets: a Review of Theory and Empirical Work，Fama, 1970。这篇论文是首次提出非常流行的“有效市场假说”概念的开创性著作，尽管现在这一理论受到很大的质疑，但是它的学术价值仍然很高。
5. The Pricing of Options and Corporate Liabilities, 1973, Black & Scholes。著名的BS公式，利用物理传热方程作为估算期权价格的起点。这也是为什么对冲基金喜欢物理系学生的原因。

---

1. Does the Stock Market Overreact? 1985, Bondt & Thaler。这篇文章质疑了有效市场假说，Bondt和Thaler提出，有统计上显着的证据表明相反的情况，投资者往往会对意外的新闻事件反应过度。这也是行为金融学的经典研究之一。行为金融学在近年来是诺奖的大热门。它的底层哲学是主观价值论和与人为本的思想。Thaler也是诺奖获得者，并在电影《大空头》中扮演了自己。
2. A closed-form GARCH option valuation model，1997， Heston & Nandi。本文提出了一种封闭式公式，用于评估现货资产，并使用广义自回归条件异方差(GARCH) 模型对其方差进行建模。由于其复杂性和实用性， GARCH 模型在 20 世纪 90 年代估计波动率方面广受欢迎，金融业也积极采用它们。
3. Optimal Execution of Portfolio Transactions，2000，Almgren & Chriss。对于每个负责完善交易执行算法的量化开发人员来说，这篇论文绝对是必读的学术文献。文章指出，价格波动来自外生性（市场本身的波动）和内生性（自己的订单对市场造成的影响）。这是一种量子效应！作者通过最小化交易成本和波动风险的组合，形式化了一种执行和衡量交易执行绩效的方法。
4. Incorporating Signals into Optimal Trading，2017，Lehalle。与 Almgren 和 Chris (2000) 的工作非常相似，本文讨论的是最佳交易执行。作者通过将马尔可夫信号纳入最优交易框架，进一步完善了该领域所做的工作，并针对带有漂移的随机过程（Ornstein-Uhlenbeck 过程）的资产特殊情况得出了最优交易策略。
5. The Performance of Mutual Funds in the Period 1945-1964, Michael Jessen。Sharpe在他的文章里提出了Beta这个概念，而Alpha这个概念，就是由Jessen在这篇论文中提出的。

---

1. Common risk factors in the returns on stocks and bonds, 1993, Eugene F. Fama。在这篇文章里，Famma提出了三因子。
2. Review of Financial Studies，2017， Stambaugh, Yuan。这篇论文出现的比较晚，因此可以把之前出现的、与因子投资相关的重要论文都评述一篇，因而就成为了我们快速了解行业的一篇重要论文。这篇文章发表比较晚，但也有了952次引用。
3. 151 Trading Strategies, 2018, Zura Kakushadze。作者来自world quant，是Alpha101的作者之一。这篇论文引用了大量的论文（2000+），也是我们进行泛读的好材料。

---

量化人必会的 NUMPY 编程 (2) - 核心语法

1. Structured Array

一开始，Numpy的数组只能存放同质的元素，即这些元素都必须有同样的数据类型。但对很多表格类数据，它们往往是由一条条记录组成的，而这些记录，又是由不同数据类型的数据组成的。比如，以最常见的行情数据来讲，它就必须至少包含时间、证券代码和OHLC等数据。

为了满足这种需求，Numpy扩展出一种名为Structured Array的数据格式。它是一种一维数组，每一个元素都是一个命名元组。

我们可以这样声明一个Structured Array:

import numpy as np
import datetime
dtypes = [
        ("frame", "O"),
        ("code", "O"),
        ("open", "f4"),
        ("high", "f4"),
        ("low", "f4"),
        ("close", "f4")
    ]
secs = np.array(
    [
        (datetime.date(2024, 3, 18), "600000", 8.9, 9.1, 8.8, 9),
        (datetime.date(2024, 3, 19), "600000", 8.9, 9.1, 8.8, 9),
    ], dtype = dtypes
)

---

在这个数据结构中，共有6个字段，它们的名字和类型通过dtype来定义。这是一个List[Tuple]类型。在初始化数据部分，它也是一个List[Tuple]。

Warning

初学者很容易犯的一个错误，就是使用List[List]来初始化Numpy Structured Array，而不是List[Tuple]类型。这会导致Numpy在构造数组时，对应不到正确的数据类型，报出一些很奇怪的错误。
比如，下面的初始化是错误的：

secs = np.array([
    [datetime.date(2024, 3, 18), "600000", 8.9, 9.1, 8.8, 9],
    [datetime.date(2024, 3, 19), "600000", 8.9, 9.1, 8.8, 9]
], dtype=dtypes)

这段代码会报告一个难懂的"Type Error: float() argument must be a string or ..."

我们使用上一节学过的inspecting方法来查看secs数组的一些特性:

print(f"secs的维度是{secs.ndim}")
print(f"secs的shape是{secs.shape}")
print(f"secs的size是{secs.size}")
print(f"secs的length是{len(secs)}")

print(f"secs[0]的类型是{type(secs[0])}")
print(f"secs[0]的维度是{secs[0].ndim}")
print(f"secs[0]的shape是{secs[0].shape}")
print(f"secs[0]的size是{secs[0].size}")
print(f"secs[0]的length是{len(secs[0])}")

可以看出，secs数组是一维数组，它的shape (2,)也正是一维数组的shape的表示法。前一节还介绍过这几个属性的关系，大家可以自行验证下是否仍然得到满足。

---

但secs的元素类型则是numpy.void，它在本质上是一个named tuple，所以，我们可以这样访问其中的任一字段：

print(secs[0]["frame"])

# 不使用列名（字段名），使用其序号也是可以的
print(secs[0][0])

我们还可以以列优先的顺序来访问其中的一个“单元格”：

print(secs["frame"][0])

对表格数据，遍历是很常见的操作，我们可以这样遍历：

for (frame, code, opn, high, low, close) in secs:
    print(frame, code, opn, high, low, close)

Numpy structured array在这部分的语法要比Pandas的DataFrame易用许多。我们在后面介绍Pandas时，还会提及这一点。

2. 运算类

2.1. 比较和逻辑运算

我们在上一节介绍定位、查找时，已经接触到了比较，比如:arr > 1。它的结果将数组中的每一个元素都与1进行比较，并且返回一个布尔型的数组。

现在，我们要扩充比较的指令：

---

函数	描述
all	如果数组中的元素全为真，返回True。可用以判断一组条件是否同时成立。
any	如果数组中至少有一个元素为真，则返回True。用以判断一组条件是否至少有一个成立
isclose	判断两个数组中的元素是否一一近似相等，返回所有的比较结果
allclose	判断两个数组中的元素是否全部近似相等
equal	判断两个数组中的元素是否一一相等，返回所有的比较结果。
not_equal	一一判断两个数组中的元素是否不相等，返回所有的比较结果
isfinite	是否为数字且不为无限大
isnan	测试是否为非数字
isnat	测试对象是否不为时间类型
isneginf	测试对象是否为负无限大
isposinf	测试对象是否为正无限大

# 开启多行输出模式
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

np.random.seed(78)
returns = np.random.normal(0, 0.03, size=4)
returns
# 判断是否全下跌
np.all(returns <= 0)
np.any(returns <= 0)

# 模拟一个起始价格为8元的价格序列
prices = np.cumprod(1+returns) * 8

# 对应的涨停价如下
buy_limit_prices = [8.03, 8.1, 8.1, 8.3]

# 判断是否涨停
np.isclose(prices, buy_limit_prices, atol=1e-2)

除了判断一个数组中的元素要么都为True，要么至少一个为True之外，有时候我们还希望进行模糊一点的判断，比如，如果过去20天中，超过60%的是收阳线，此时我们可以用np.count_nonzero，或者np.sum来统计数组中为真的情况：

---

np.count_nonzero(returns > 0)
np.sum(returns > 0)

在上一节进行比较的示例中，我们都只使用了单个条件。如果我们要按多个条件的组合进行查找，就需要依靠逻辑运算来实现。

在Numpy中，逻辑运算既可以通过函数、也可以通过运算符来完成：

函数	运算符	描述	python等价物
logical_and	&	执行逻辑与操作	and
logical_or	|	执行逻辑或操作	or
logical_not	~	执行逻辑或操作	not
logical_xor	'^'	执行逻辑异或操作	xor

逻辑运算有什么用呢？比如我们在选股时，有以下表格数据：

股票	pe	mom
AAPL	30.5	0.1
GOOG	32.3	0.3
TSLA	900.1	0.5
MSFT	35.6	0.05

上述表格可以用Numpy的Structured Array来表示为：

tickers = np.array([
    ("APPL", 30.5, 0.1),
    ("GOOG", 32.3, 0.3),
    ("TSLA", 900.1, 0.5),
    ("MSFT", 35.6, 0.05)
], dtype=[("ticker", "O"), ("pe", "f4"), ("mom", "f4")])

现在，我们要找出求PE < 35, 动量 (mom) > 0.2的记录，那么我们可以这样构建条件表达式：

---

(tickers["pe"] < 35) & (tickers["mom"] > 0.2)

Numpy会把pe这一列的所有值跟35进行比较，然后再与mom与0.2比较的结果进行逻辑与运算，这相当于：

np.array((1,1,0,0)) & np.array((0, 1, 1, 0))

在Numpy中，True与1的值在做逻辑运算时是相等的；0与False也是。

如果不借助于Numpy的逻辑操作，我们就要用Python的逻辑操作。很不幸，这必须使用循环。如果计算量大，这将会比较耗时间。

在量化中使用异或操作的例子仍然最可能来自于选股。比如，如果我们要求两个选股条件，只能有一个成立时，才买入；否则不买入，就可以使用异或运算。

2.2. 集合运算

在交易中，我们常常要执行调仓操作。做法一般是，选确定新的投资组合，然后与当前的投资组合进行比较，找出需要卖出的股票，以及需要买入的股票。这个操作，就是集合运算。在Python中，我们一般是通过set语法来实现。

在Numpy中，我们可以使用通过以下方法来实现集合运算：

import numpy as np

# 创建两个一维数组
x = np.array([1, 2, 3, 4, 5])
y = np.array([4, 5, 6, 7, 8])

# 计算交集
intersection = np.intersect1d(x, y)
print("Intersection (交集):", intersection)

# 计算并集
union = np.union1d(x, y)
print("Union (并集):", union)

---

diff = np.setdiff1d(x, y)
print("x - y:", diff)

此外，我们还可能使用in1d(a1, a2)方法来判断a1 中的元素是否都在 a2 中存在。比如，在调仓换股中，如果当前持仓都在买入计划中，则不需要执行调仓。

2.3. 数学运算和统计

Numpy中数学相关的运算有线性代数运算（当然还有基本代数运算）、统计运算、金融指标运算等等。

2.3.1. 线性代数

线性代数在量化中有重要用途。比如，在现代资产组合理论（MPT）中，我们要计算资产组合收益率及协方差，都要使用矩阵乘法。大家可以参考投资组合理论与实战系列文章，下面是其中的一段代码：

...
cov = np.cov(port_returns.T)
port_vol = np.sqrt(np.dot(np.dot(weights, cov), weights.T))

矩阵乘法是线性代数中的一个核心概念，它涉及到两个矩阵的特定元素按照规则相乘并求和，以生成一个新的矩阵。具体来说，如果有一个矩阵A 为 \(m \times n\) 维，另一个矩阵B 为 \(n \times p\) 维，那么它们的乘积 \(C = AB\)将会是一个\(m \times p\)维的矩阵。乘法的规则是A的每一行与B的每一列对应元素相乘后求和。

下面通过一个具体的例子来说明矩阵乘法的过程：

假设我们有两个矩阵A和B：

---

$$ A = \begin{bmatrix} 2 & 3 \ 1 & 4 \end{bmatrix} $$ 和 $$ B = \begin{bmatrix} 1 & 2 \ 3 & 1 \end{bmatrix} $$ 要计算AB，我们遵循以下步骤：

取A的第一行 \((2, 3)\) 与的第一列\((1,3)\) 相乘并求和得到\(C_{11} = [2\times1 + 3\times3 = 11]\)

同理，取A的第一行与B的第二列\((2, 1)\)相乘并求和得到\(C_{12} = [2\times2 + 3\times1 = 7]\)

取A的第二行\((1, 4)\)与B的第一列相乘并求和得到\(C_{21} = [1\times1 + 4\times3 = 13]\)

取A的第二行与B的第二列相乘并求和得到\(C_{22} = [1\times2 + 4\times1 = 5]\)

因此，矩阵C = AB为：

\[ C = \begin{bmatrix} 11 & 7 \\ 13 & 6 \ \end{bmatrix} \]

与代数运算不同，矩阵乘法不满足交换律，即一般情况下\(AB \neq BA\)。

在Numpy中，我们可以使用np.dot()函数来计算矩阵乘法。

---

上述示例使用numpy来表示，即为：

A = np.array([[2,3],[1,4]])
B = np.array([[1,2],[3,1]])

np.dot(A, B)

最终我们将得到与矩阵C相同的结果。

除此之外，矩阵逆运算(np.linalg.inv)在计算最优投资组合权重时，用于求解方程组，特征值和特征向量(np.linalg.eig, np.linalg.svd)在分析资产回报率的主成分，进行风险分解时使用。

2.3.2. 统计运算

常用的统计运算包括：

函数	描述
np.mean	计算平均值
np.median	计算中位数
np.std	计算标准差
np.var	计算方差
np.min	计算最小值
np.max	计算最大值
np.percentile	用于计算历史数据的分位点
np.quantile	用于计算历史数据的分位数，此函数与percentile功能相同
np.corr	用于计算两个变量之间的相关性

np.percentile与np.quantile功能相同，都是用于计算分位数。两者在参数上略有区别。

---

当我们对同一数组，给quantile传入分位点0.25时，如果给percentile传入分位点25时，两者的结果将完全一样。也就是后者要乘以100。在量化交易中，quantile用得可能会多一些。

np.percentile（或者np.quantile）的常见应用是计算25%, 50%和75%的分位数。用来绘制箱线图（Boxplot）。

此外，我们也常用它来选择自适应参数。比如，在RSI的应用中，一般推荐是低于20（或者30）作为超卖，此时建议买入；推荐是高于80（或者70）作为超买，此时建议卖出。但稍微进行一些统计分析，你就会发现这些阈值并不是固定的。如果我们以过去一段时间的RSI作为统计，找出它的95%分位作为卖点，15%作为买点，往往能得到更好的结果。

2.3.3. 量化指标的计算

有一些常用的量化指标的计算，也可以使用Numpy来完成，比如，计算移动平均线，就可以使用Numpy提供的convolve函数。

import numpy as np
def moving_average(data, window_size):
    return np.convolve(data, np.ones(window_size)/window_size, 'valid')

当然，很多人习惯使用talib，或者pandas的rolling函数来进行计算。convolve（卷积）是神经网络CNN的核心，正是这个原因，我们这里提一下。

np.convolve的第二个参数，就是卷积核。这里我们是实现的是简单移动平均，所以，卷积核就是一个由相同的数值组成的数组，它们的长度就是窗口大小，它们的和为1。

---

如果我们把卷积核替换成其它值，还可以实现WMA等指标。从信号处理的角度看，移动平均是信号平滑的一种，使用不同的卷积核，就可以实现不同的平滑效果。

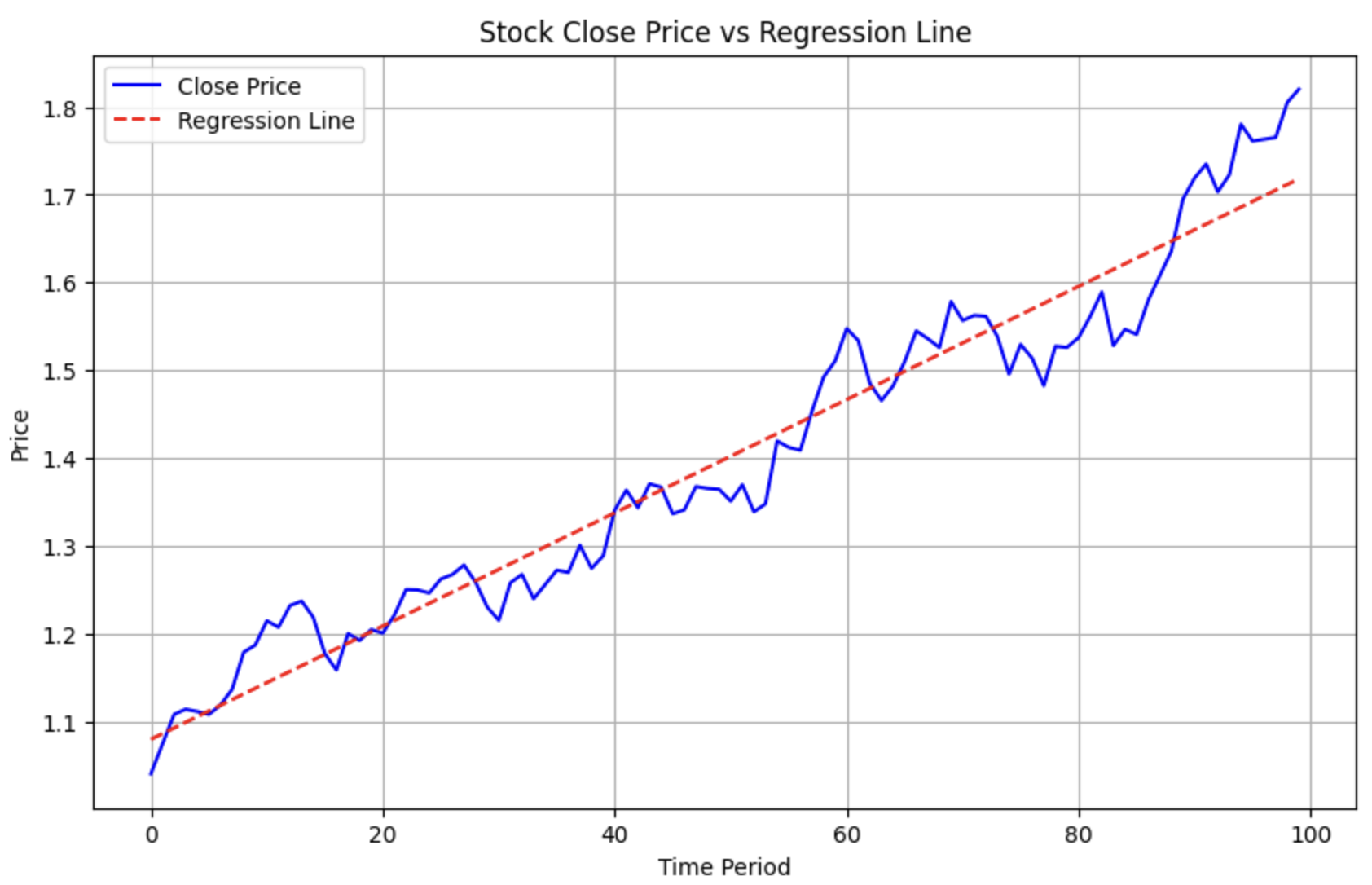
在量化中，还有一类计算，这里也提一下，就是多项式回归。比如，某两支股票近期都呈上升趋势，我们想知道哪一支涨得更好？这时候我们就可以进行多项式回归，将其拟合成一条直线，再比较它们的斜率。

下面的代码演示了如何使用Numpy进行多项式回归。

import numpy as np
import matplotlib.pyplot as plt

returns = np.random.normal(0, 0.02, size=100)
alpha = 0.01
close = np.cumprod(1 + returns + alpha)

a, b = np.polyfit(np.arange(100), close, deg=1)

# 继续之前的代码

# 使用a, b构建回归线的y值
regression_line = a * np.arange(100) + b

# 绘制原始的close曲线
plt.figure(figsize=(10, 6))
plt.plot(close, label='Close Price', color='blue')

# 绘制回归线
plt.plot(regression_line, label='Regression Line', color='red', linestyle='--')

# 添加图例、标题和坐标轴标签
plt.title('Stock Close Price vs Regression Line')
plt.xlabel('Time Period')
plt.ylabel('Price')
plt.legend()

# 显示图表
plt.grid(True)
plt.show()

---

这将生成下图：

3. 类型转换和Typing

在不同的库之间交换数据，常常会遇到格式问题。比如，我们从第三方数据源拿到的行情数据，它们用的时间字段常常会是字符串（这是代码少写了几行吗？！）。有一些库在存储行情时，对OHLC这些字段进行了优化，使用了4个字节的浮点数，但如果要传给talib进行指标计算，就必须先转换成8个字节的浮点数，等等，这就有了类型转换的需求。

此外，我们还会遇到需要将numpy数据类型转换为python内置类型，比如，将numpy.float64转换为float的情况。

---

3.1. Numpy内部类型转换

Numpy内部类型转换，我们只需要使用astype函数即可。

x = np.array(['2023-04-01', '2023-04-02', '2023-04-03'])
print(x.astype(dtype='datetime64[D]'))

x = np.array(['2014', '2015'])
print(x.astype(np.int32))

x = np.array([2014, 2015])
print(x.astype(np.str_))

Tips

如何将boolean array转换成整数类型，特别是，将True转为1，False转为-1？ 在涉及到阴阳线的相关计算中，我们常常需要将 open > close这样的条件转换为符号1和-1，以方便后续计算。这个转换可以用：

>>> x = np.array([True, False])
>>> x * 2 - 1
... array([ 1, -1])

3.2. Numpy类型与Python内置类型转换

如果我们要将Numpy数组转换成Python数组，可以使用tolist函数。

x = np.array([1, 2, 3])
print(x.tolist())

我们通过item()函数，将Numpy数组中的元素转换成Python内置类型。

x = np.array(['2023-04-01', '2023-04-02'])
y = x.astype('M8[s]')
y[0].item()

---

Warning

一个容易忽略的事实是，当我们从Numpy数组中取出一个标量时，我们都应该把它转换成为Python对象后再使用。否则，会发生一些隐藏的错误，比如下面的例子：

import json
x = np.arange(5)
print(json.dumps([0]))
print(x[0])

json.dumps([x[0]])

这里最后一行会出错。提示type int64 is not JSON serializable。把最后一行换成json.dumps([x[0].item()])则可以正常执行。

3.3. Typing

从Python 3.1起，就开始引入类型注解(type annotation)，到Python 3.8，基本上形成了完整的类型注解体系。我们经常看到函数的参数类型注解，比如，下面的代码:

from typing import List
def add(a: List[int], b: int) -> List[int]:
    return [i + b for i in a]

从此，Python代码也就有了静态类型检查支持。

NumPy的Typing模块提供了一系列类型别名（type aliases）和协议（protocols），使得开发者能够在类型注解中更精确地表达NumPy数组的类型信息。这有助于静态分析工具、IDE以及类型检查器提供更准确的代码补全、类型检查和错误提示。

这个模块提供的主要类型是ArrayLike, NDArray和DType。

---

import numpy
from numpy.typing import ArrayLike, NDArray, DTypeLike
import numpy as np

def calculate_mean(data: ArrayLike) -> float:
    """计算输入数据的平均值，数据可以是任何ArrayLike类型"""
    return np.mean(data)

def add_one_to_array(arr: NDArray[np.float64]) -> NDArray[np.float64]:
    """向一个浮点数数组的每个元素加1，要求输入和输出都是np.float64类型的数组"""
    return arr + 1

def convert_to_int(arr: NDArray, dtype: DTypeLike) -> NDArray:
    """将数组转换为指定的数据类型"""
    return arr.astype(dtype)

如果你是在像vscode这样的IDE中使用上述函数，你就可以看到函数的类型提示。如果传入的参数类型不对，还能在编辑期间，就得到错误提示。

4. 拓展阅读

4.1. Numpy的数据类型

在Numpy中，有以下常见数据类型。每一个数字类型都有一个别名。在需要传入dtype参数的地方，一般两者都可以使用。另外，别名在字符串类型、时间和日期类型上，支持得更好。比如，'S5'是Ascii码字符串别外，它除了指定数据类型之外，还指定了字符串长度。datetime64[S]除了表明数据是时间日期类型之外，还表明它的精度到秒。

---

类型	别名	类别	别名
np.int8	i1	np.float16	f2
np.int16	i2	np.float32	f4，还可指定结尾方式，比如'f4'表示大端字节序。其它float类型同。
np.int32	i4	np.float64	f8
np.int64	i8	np.float128	f16
np.uint8	u1	np.bool_	b1
np.uint16	u2	np.str_	U (后接长度，例如U10)
np.uint32	u4	np.bytes_	S (后接长度，例如S5)
np.uint64	u8		np.datetime64
np.timedelta64	m8和m8[D] m8[h] m8[m] m8[s]等

---

《因子投资与机器学习策略》开课啦！

---

9月8日晚，在线直播，不见不散

---