others »

[0825] QuanTide Weekly

#others #weekly #career

Table of Content

本周要闻¶

美联储主席鲍威尔表示，美联储降息时机已经到来
摩根大通港股仓位近日大量转仓，涉及市值超1.1万亿港元

下周看点¶

广发明星基金经理刘格菘的首只“三年持有基”即将到期，亏损超58%
周四A50指数交割日、周五本月收官日
周六发布8月官方制造PMI

本周精选¶

如何实现Alpha 101？
高效量化编程 - Mask Array and Find Runs
样本测试之外，我们还有哪些过拟合检测方法？

要闻详情¶

美联储主席鲍威尔表示，通货膨胀率仅比美联储2%的目标高出半个百分点，失业率也在上升，“政策调整的时机已经到来”。财联社
摩根大通港股仓位近日大量转仓，涉及市值超1.1万亿港元。转仓后，券端持股市值排名由第4名下跌至14名，持股市值不足2000亿港元。1个月前，摩根大通亦有超6000亿元转仓。金融界
广发基金明星基金经理刘格菘的首只“三年持有基”即将到期，初期募资148.70亿元，截至今年8月22日，该基金（A/C）成立以来亏损超58%。近期，三年持有期基金集中到期。回溯来看，三年持有期主动权益基金在2021年——2022年间，公募基金行业密集推出了至少73只三年持有期主动权益基金。打开封闭之后，基民会不会巨量赎回？这是下周最重要的波动因素之一。相信有关方面已经做好了准备。新浪财经
8月25日，北京商报发表《外资今天对A投爱答不理，明天就让他们高攀不起》一周年。在一年前的这篇评论中，北京商报指出，在目前股票具有极高投资价值的阶段，有一些外资流出A股，可能就是他们所谓的技术派典型代表，对指数患得患失，但他们最终一定会后悔，等想再回来的时候，势必要支付更高的价格，正所谓今天对A股爱答不理，明天就让他们高攀不起。该评论发布次日，沪指开盘于3219点。一年之后，沪指收盘于2854点。

如何实现Alpha 101？¶

2015 年，World Quant 发布了报告《101 Formulaic Alphas》，它包含了 101 种不同的股票选择因子，这些因子中，有 80%是当时正在 World Quant 交易中使用的因子。该报告发表之后，在产业界引起较大反响。

目前，根据 Alpha101 生成的因子库，已几乎成为各量化平台、数据提供商和量化机构的必备。此外，一些机构受此启发，还在此基础上构建了更多因子，比如国泰君安推出的 Alpha 191 等。这两个因子库都有机构进行了实现。比如 DolphinDB 和聚宽都提供了这两个因子库。

这篇文章就来介绍如何读懂《101 Formulaic Alphas》并且实现它。文章内容摘自我们的课程《因子分析与机器学习策略》的第8课，篇幅所限，有删节。

Alpha 101 因子中的数据和算子¶

在实现 Alpha101 因子之前，我们首先要理解其公式中使用的数据和基础算子。

Alpha101 因子主要是基于价格和成交量构建，只有少部分 Alpha 中使用了基本面数据，包括市值数据和行业分类数据 [^fundmental_data]。

Tip

在 A 股市场，由于财报数据的可信度问题 [^fraut]，由于缺乏 T+0 和卖空等交易机制，短期内由交易行为产生的价格失效现象非常常见。因此，短期量价因子在现阶段的有效性高于基本面因子。

在价量数据中，Alpha101 依赖的最原始数据是 OHLC, volume（成交额）, amount（成交量），turnover（换手率），并在此基础上，计算出来 returns（每日涨跌幅）和 vwap（加权平均成交价格）。

returns 和 vwap 的计算方法如下：

# THE NUMPY WAY
vwap = bars["amount"] / bars["volume"] / 100
returns = bars["close"][1:]/bars["close"][:-1] - 1

# THE PANDAS WAY
vwap = df.amount / df.volume / 100
returns = df.close.pct_change()

除此之外，要理解 Alpha101，重要的是理解它的公用算子。在 Alpha101 中，总共有约 30 个左右的算子，其中有一些像 abs, log, sign, min, max 以及数学运算符（+, -, *, /）等都是无须解释的。

下面，我们就先逐一解释需要说明的算子。

三目运算符¶

三目运算符是 Python 中没有，但存在于 C 编程语言的一个算子。这个运算符可以表示为："x ? y : z"，它相当于 Python 中的：

expr_result = None

if x:
    expr_result = y
else:
    expr_result = z

rank¶

在 Alpha101 中，存在两个 rank，一个是横截面上的，即对同一时间点上 universe 中所有的股票进行排序；另一个是时间序列上的，即对同一股票在时间序列上的排序。

在横截面上的 rank 直接调用 DataFrame 的 rank。比如，

import pandas as pd

data = {
    'asset': ["000001", "000002", "000004", "000005", "000006"],
    'factor': [85, 92, 78, 92, 88],
    'date': [0] * 5
}
df = pd.DataFrame(data).set_index('date').pivot(index=None, columns="asset", values="factor")

def rank(df):
    return df.rank(axis=1, pct=True, method='min')

在上面这段代码中，date 为索引，列名字为各 asset，factor 为其值，此时，我们就可以通 rank(axis=1) 的方法，对各 asset 的 factor 值在截面上进行排序。当我们使用 axis=1 参数时，索引是不参与排序。pct 为 True 表示返回的是百分比排名，False 表示返回的是排名。

有时候我们也需要在时间序列上进行排序，在 Alpha101 中，这种排序被定义为 ts_rank，通过前缀 ts_来与截面上的 rank 相区分。此后，当我们看到 ts_前缀时，也应该作同样理解。

from bottleneck import move_rank

def ts_rank(df, window=10, min_count=1):
    return move_rank(df, window, axis=0, min_count=min_count)

在这里我们使用的是 bottleneck 中的 move_rank，它的速度要显著高于 pandas 和 scipy 中的同类实现。如果使用 pandas 来实现，代码如下：

def rolling_rank(na):
    return rankdata(na,method='min')[-1]

def ts_rank(df, window=10):
    return df.rolling(window).apply(rolling_rank)

注意第 3 行中的 [-1] 是必须的。

rank 和 ts_rank 的使用在 alpha004 因子中的应用最为典型。这个因子是：

# ALPHA#4    (-1 * TS_RANK(RANK(LOW), 9))
def alpha004(low):
    return -1 * ts_rank(rank(low), 9)

在这里，参数 low 是一个以 asset 为列、日期为索引，当日最低价为值的 dataframe，是一个宽表。下面，我们看一下对参数 low 依次调用 rank 和 ts_rank 的结果。通过深入几个示例之后，我们就很快能够明白 Alpha101 的因子计算过程。

from bottleneck import move_rank
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

df = pd.DataFrame(
       [[6.18, 19.36, 33.13, 14.23,  6.8 ,  6.34],
       [6.55, 20.36, 32.69, 14.52,  6.4,  6.44 ],
       [7.  , 20.79, 32.51, 14.56,  6.0 ,  6.54],
       [7.06, 21.35, 33.13, 14.47,  6.5,  6.64],
       [7.03, 21.56, 33.6 , 14.6 ,  6.5,  6.44]], 
       columns=['000001', '000002', '000063', '000066', '000069', '000100'], 
       index=['2022-01-04', '2022-01-05', '2022-01-06', '2022-01-07', '2022-01-10'])

def rank(df):
    return df.rank(axis=1, pct=True, method='min')

def ts_rank(df, window=10, min_count=1):
    return move_rank(df, window, axis=0, min_count=min_count)

df
rank(df)

-1 * ts_rank(rank(df), 3)

示例将依次输出三个 DataFrame。我们看到，rank 是执行在行上，它将各股票按最低价进行排序；ts_rank 执行在列上，对各股票在横截面上的排序再进行排序，反应出最低位置的变化。

比如，000100 这支股票，在 2022 年 1 月 4 日，横截面的排位在 33%分位，到了 1 月 10 日，它在横截面上的排位下降到 16.7%。

通过 ts_rank 之后，最终它在 1 月 10 日的因子值为 1，反应了它在横截面上排位下降的事实。同理，000001 这支股票，在 1 月 4 日，它的横截面上的排位是 16.7%（最低），而在 1 月 5 日，它的排序上升到 50%，最终它在当日的因子值为-1，反应了它在横截面排序上升的事实。

Tip

通过 Alpha004 因子，我们不仅了解到 rank 与 ts_rank 的用法，也知道了横截面算子与时序算子的区别。此外，我们也了解到，为了方便计算 alpha101 因子，最佳的数据组织方式可能是将基础数据（比如 OHLC）都组织成一个个以日期为索引、asset 为列的宽表，以方便在两个方向上（横截面和时序）的计算。

ts_*¶

这一组算子中，除了之前已经介绍过的 ts_rank 之外，还有 ts_max, ts_argmax, ts_argmin, ts_min。这一些算子都有两个参数，首先时时间序列，比如 close 或者 open，然后是滑动窗口的长度。

注意这一类算子一定是在滑动窗口上进行的，只有这样，才不会引入未来数据。

除此之外，其它常用统计函数，比如 min, max, sum, product, stddev 等，尽管没有使用 ts_前缀，它们也是时序算子，而不是截面算子。考虑到我们已经通过 ts_rank 详细介绍了时序算子的用法，而这些算子的作用大家也都非常熟悉，这里就从略。

delay¶

在 Alpha101 中，delay 算子用来获取 n 天前的数据。比如，

def delay(df, n):
    return df.shift(n)

data = {
    'date': pd.date_range(start='2023-01-01', periods=10),
    'close': [100, 101, 102, 103, 104, 105, 106, 107, 108, 109]
}
df = pd.DataFrame(data)

delay(df, 5)

如此一来，我们在计算第 5 天的因子时，使用的 close 数据就是 5 天前的，即原来索引为 0 处的 close。

correlation 和 covariance¶

correlation 就是两个时间序列在滑动窗口上的皮尔逊相关系数，这个算子可以实现为：

def correlation(x, y, window=10):
    return x.rolling(window).corr(y).fillna(0).replace([np.inf, -np.inf], 0)

def covariance(x, y, window=10):
    return x.rolling(window).cov(y)

注意在这里，尽管我们只对 x 调用了 rolling，但在计算相关系数时，经验证，y 也是按同样的窗口进行滑动的。

scale¶

按照 Alpha101 的解释，这个算子的作用，是将数组的元素进行缩放，使之满足 sum(abs(x)) = a，缺省情况下 a = 1。它可以实现为：

def scale(df, k=1):
    return df.mul(k).div(np.abs(df).sum())

decay_linear¶

这个算子的作用是将长度为 d 的时间序列中的元素进行线性加权衰减，使之总和为 1，且越往后的元素权重越大。

def decay_linear(df, period=10):
    weights = np.array(range(1, period+1))
    sum_weights = np.sum(weights)
    return df.rolling(period).apply(lambda x: np.sum(weights*x) / sum_weights)

delta¶

相当于 dataframe.diff()。

adv{d}¶

成交量的 d 天简单移动平均。

signedpower¶

signedpower(x, a) 相当于 x^a

Alpha 101 因子解读¶

此部分略

开源的Alpha101因子分析库¶

完整探索Alpha101中的定义的因子的最佳方案是，根据历史数据，计算出所有这些因子，并且通过Alphalens甚至backtrader对它们进行回测。popbo就实现了这样的功能。

运行该程序库需要安装alphalens, akshare，baostock以及jupyternotebook。在进行研究之前，需要先参照其README文件进行数据下载和因子计算。然后就可以打开research.ipynb，对每个因子的历年表现进行分析。

在我们的补充材料中，提供了该项目的全部源码并且可以在我们的课程环境中运行。

高效量化编程 - Mask Array and Find Runs¶

在很多量化场景下，我们都需要统计某个事件连续发生了多少次，比如，连续涨跌停、N连阳、计算Connor's RSI中的streaks等等。

比如，要判断下列收盘价中，最大的连续涨停次数是多少？最长的N连涨数是多少？应该如何计算呢？

a = [15.28, 16.81, 18.49, 20.34, 21.2, 20.5, 22.37, 24.61, 27.07, 29.78, 
     32.76, 36.04]

假设我们以10%的涨幅为限，则可以将上述数组转换为：

pct = np.diff(a) / a[:-1]
pct > 0.1

我们将得到以下数组：

flags = [True, False, True, False, False, False, True, False, True, True, True]

这仍然不能计算出最大连续涨停次数，但它是很多此类问题的一个基本数据结构，我们将原始的数据按条件转换成类似的数组之后，就可以使用下面的神器了：

from numpy.typing import ArrayLike
from typing import Tuple
import numpy as np

def find_runs(x: ArrayLike) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
    """Find runs of consecutive items in an array.
    """

    # ensure array
    x = np.asanyarray(x)
    if x.ndim != 1:
        raise ValueError("only 1D array supported")
    n = x.shape[0]

    # handle empty array
    if n == 0:
        return np.array([]), np.array([]), np.array([])

    else:
        # find run starts
        loc_run_start = np.empty(n, dtype=bool)
        loc_run_start[0] = True
        np.not_equal(x[:-1], x[1:], out=loc_run_start[1:])
        run_starts = np.nonzero(loc_run_start)[0]

        # find run values
        run_values = x[loc_run_start]

        # find run lengths
        run_lengths = np.diff(np.append(run_starts, n))

        return run_values, run_starts, run_lengths


pct = np.diff(a) / a[:-1]
v,s,l = find_runs(pct > 0.099)
(v, s, l)

输出结果为：

(array([ True, False,  True]), array([0, 3, 6]), array([3, 3, 5]))

输出结果是一个由三个数组组成的元组，分别表示：

value: unique values start: start indices length: length of runs 在上面的输出中，v[0]为True，表示这是一系列涨停的开始，s[0]则是对应的起始位置，此时索引为0; l[0]则表示该连续的涨停次数为3次。同样，我们可以知道，原始数组中，最长连续涨停（v[2]）次数为5（l[2]），从索引6（s[2]）开始起。

所以，要找出原始序列中的最大连续涨停次数，只需要找到l中的最大值即可。但要解决这个问题依然有一点技巧，我们需要使用第4章中介绍的 mask array。

v_ma = np.ma.array(v, mask = ~v)
pos = np.argmax(v_ma * l)
print(f"最大连续涨停次数{l[pos]}，从索引{s[pos]}:{a[s[pos]]}开始。")

在这里，mask array的作用是，既不让 v == False 的数据参与计算（后面的 v_ma * l），又保留这些元素的次序（索引）不变，以便后面我们调用 argmax 函数时，找到的索引跟v, s, l中的对应位置是一致的。

我们创建的v_ma是一个mask array，它的值为：

masked_array(data=[True, --, True],
            mask=[False,  True, False],
            fill_value=True)

当它与另一个整数数组相乘时，True就转化为数字1，这样相乘的结果也仍然是一个mask array:

masked_array(data=[3, --, 5],
             mask=[False,  True, False],
            fill_value=True)

当arg_max作用在mask array时，它会忽略掉mask为True的元素，但保留它们的位置，因此，最终pos的结果为2，对应的 v,s,l中的元素值分别为: True, 6, 5。

如果要统计最长N连涨呢？这是一个比寻找涨停更容易的任务。不过，这一次，我们将不使用mask array来实现：

v,s,l = find_runs(np.diff(a) > 0)

pos = np.argmax(v * l)
print(f"最长N连涨次数{l[pos]}，从索引{s[pos]}:{a[s[pos]]}开始。")

输出结果是：最长N连涨次数6，从索引5:20.5开始。

这里的关键是，当Numpy执行乘法时，True会被当成数字1，而False会被当成数字0，于是，乘法结果自然消除了没有连续上涨的部分，从而不干扰argmax的计算。

当然，使用mask array可能在语义上更清楚一些，尽管mask array的速度会慢一点，但正确和易懂常常更重要。

计算 Connor's RSI中的streaks Connor's RSI（Connor's Relative Strength Index）是一种技术分析指标，它是由Nirvana Systems开发的一种改进版的相对强弱指数（RSI）。

Connor's RSI与传统RSI的主要区别在于它考虑了价格连续上涨或下跌的天数，也就是所谓的“连胜”（winning streaks）和“连败”（losing streaks）。这种考虑使得Connor's RSI能够更好地反映市场趋势的强度。

在前面介绍了find_runs函数之后，计算streaks就变得非常简单了。

def streaks(close):
    result = []
    conds = [close[1:]>close[:-1], close[1:]<close[:-1]]

    flags = np.select(conds, [1, -1], 0)
    v, _, l = find_runs(flags)
    for i in range(len(v)):
        if v[i] == 0:
            result.extend([0] * l[i])
        else:
            result.extend([v[i] * x for x in range(1, (l[i] + 1))])

    return np.insert(result, 0, 0)

这段代码首先将股价序列划分为上涨、下跌和平盘三个子系列，然后对每个子系列计算连续上涨或下跌的天数，并将结果合并成一个新的数组。

在streaks中，连续上涨天数要用正数表示，连续下跌天数用负数表示，所以在第5行中，通过np.select将条件数组转换为[1, 0, -1]的序列，后面使用乘法就能得到正确的连续上涨（下跌）天数了。

样本测试之外，我们还有哪些过拟合检测方法？¶

在知乎上看到一个搞笑的贴子，说是有人为了卖策略，让回测结果好看，会在代码中植入大量的if 语句，判断当前时间是特定的日期，就不进行交易。但奥妙全在这些日期里，因为在这些日期时，交易全是亏损的。

内容的真实性值得怀疑。不过，这却是一个典型的过拟合例子。

过拟合和检测方法¶

过拟合是指模型与数据拟合得很好，以至于该模型不可泛化，从而不能在另一个数据集上工作。从交易角度来说，过拟合“设计”了一种策略，可以很好地交易历史数据，但在新数据上肯定会失败。

过拟合是我们在回测中的头号敌人。如何检测过拟合呢？

一个显而易见的检测方法是样本外测试。它是把整个数据集划分为互不重叠的训练集和测试集，在训练集上训练模型，在测试集上进行验证。如果模型在测试集上也表现良好，就认为该模型没有拟合。

在样本本身就不足的情况下，样本外测试就变得困难。于是，人们发明了一些拓展版本。

其中一种拓展版本是 k-fold cross-validation，这是在机器学习中常见的概念。

它是将数据集随机分成 K 个大小大致相等的子集，对于每一轮验证，选择一个子集作为验证集，其余 K-1 个子集作为训练集。模型在训练集上训练，在验证集上进行评估。这个过程重复 K 次，最终评估指标通常为 K 次验证结果的平均值。

这个过程可以简单地用下图表示：

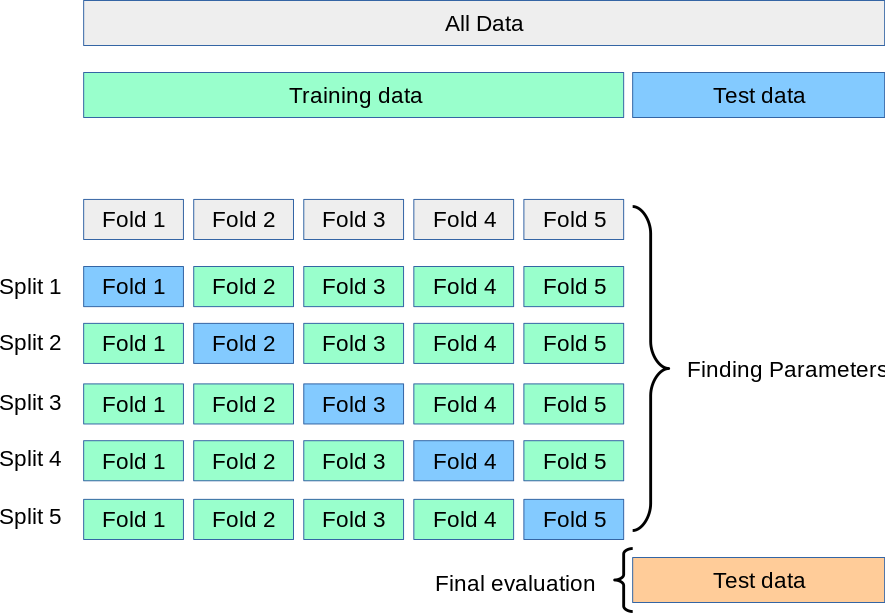
k-fold cross validation，by sklearn

但在时间序列分析（证券分析是其中典型的一种）中，k-fold方法是不适合的，因为时间序列分析有严格的顺序性。因此，从k-fold cross-validation特化出来一个版本，称为 rolling forecasting。你可以把它看成顺序版本的k-fold cross-validation。

它可以简单地用下图表示：

rolling forecasting, by tsfresh

从k-fold cross-validation到rolling forecasting的两张图可以看出，它们的区别在于一个是无序的，另一个则强调时间顺序，训练集和验证集之间必须是连续的。

有时候，你也会看到 Walk-Forward Optimization这种说法。它与rolling forecasting没有本质区别。

不过，我最近从buildalpha网站上，了解到了一种新颖的方法，这就是噪声测试。

新尝试：噪声测试¶

buildalpha的噪声测试，是将一定比率的随机噪声叠加到回测数据上，然后再进行回测，并将基于噪声的回测与基于真实数据的回测进行比较。

L50

它的原理是，在我们进行回测时，历史数据只是可能发生的一种可能路径。如果时间重演，历史可能不会改变总的方向，但是偶然性会改变历史的步伐。而一个好的策略，应该是能对抗偶然性、把握历史总的方向的策略。因此，在一个时间序列加上一些巧妙的噪声，就可能会让过拟合的策略失效，而真正有效的策略仍然闪耀。

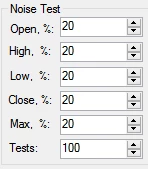
buildalpha是一个类似tradingview的平台。要进行噪声测试，可以通过图形界面进行配置。

通过这个对话框，buildalpha修改了20%左右的数据，并且对OHLC的修改幅度都控制在用ATR的20%以内。最下面的100表明我们将随机生成100组带噪声的数据。

我们对比下真实数据与叠加噪声的数据。

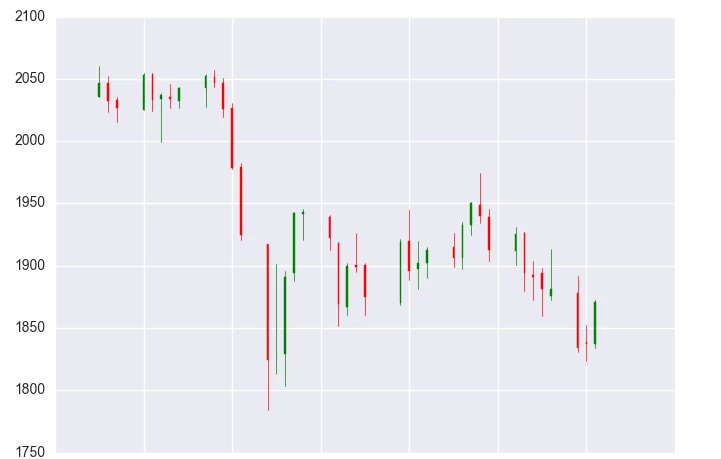
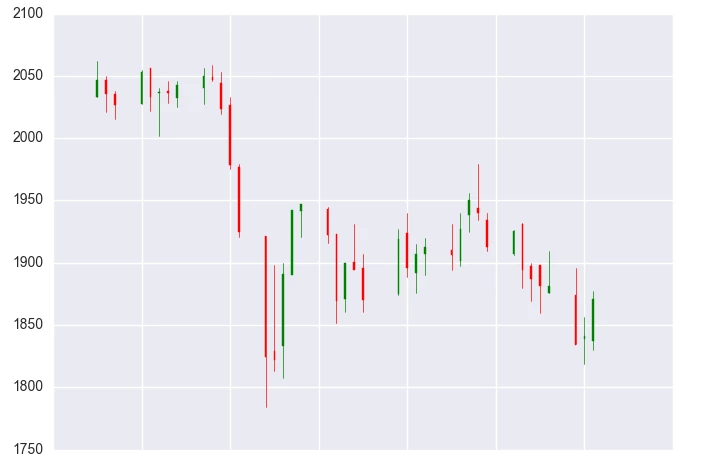
左图为真实数据，右图为叠加部分噪声的数据。叠加噪声后，在一些细节上，引入了随机性，但并没有改变股价走势（叠加是独立的）。如果股价走势被改变，那么这种方法就是无效的甚至有害的。

最后，在同一个策略上，对照回测的结果是：

75%

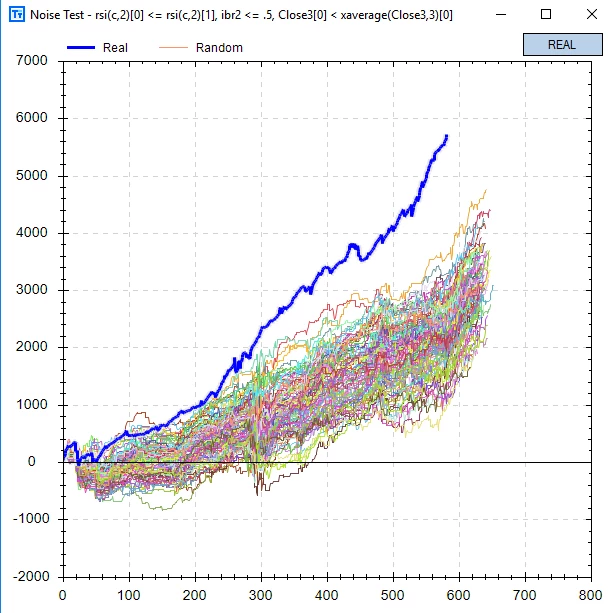
从结果上看，在历史的多条可能路径中，没有任何一条的回测结果能比真实数据好。

换句话说，真实回测的结果之所以这么好，纯粹是因为制定策略的人，是带着上帝视角，从未来穿越回去的。

参数平原与噪声测试¶

噪声测试是稍稍修改历史数据再进行圆滑。而参数平原则是另一种检测过拟合的方法，它是指稍微修改策略参数，看回测表现是否会发生剧烈的改变。如果没有发生剧烈的改变，那么策略参数就是鲁棒的。

Build Alpha以可视化的方式，提供了参数平原检测。

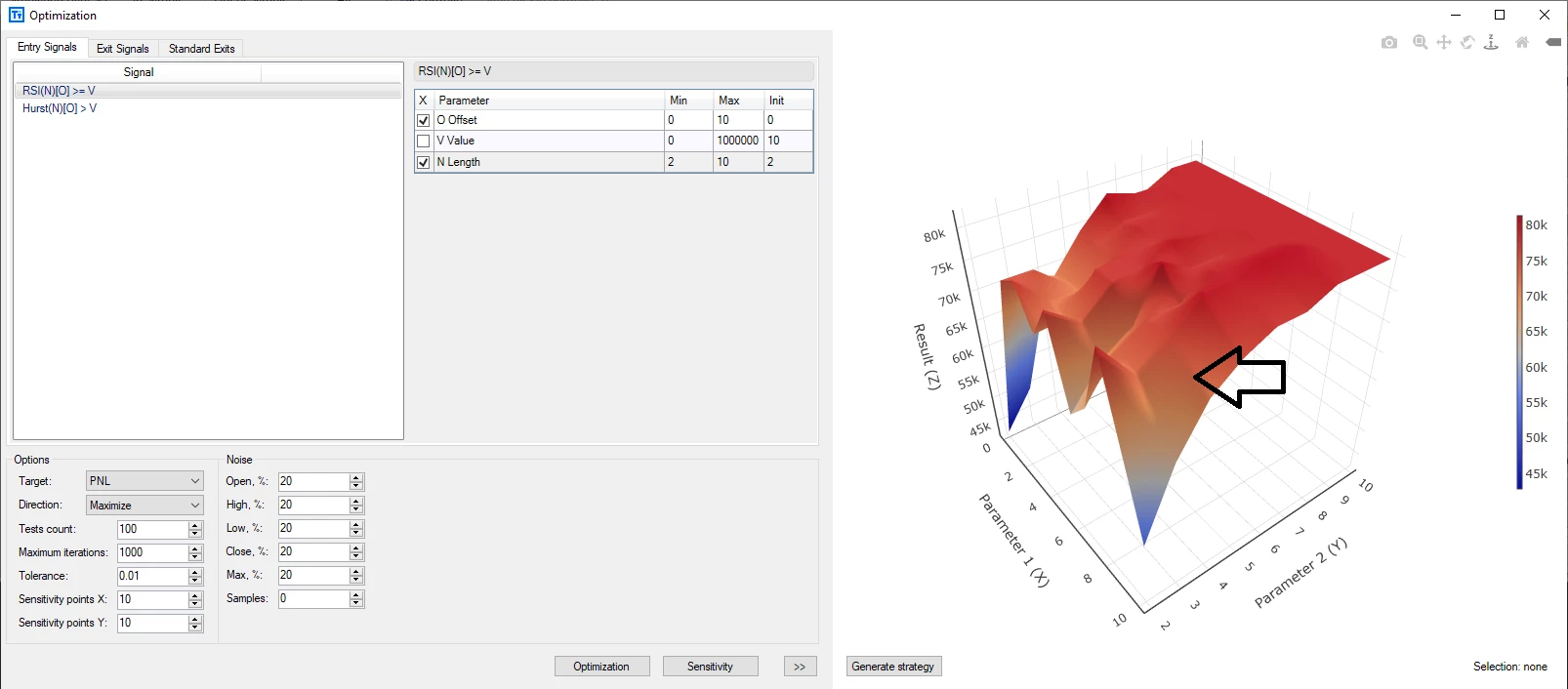
在这个3D图中，参数选择为 X= 9和Y=4,如黑色简单所示。显然，这一区域靠近敏感区域，在其周围，策略的性能下降非常厉害。按照传统的推荐，我们应该选择参数 X=8和Y=8，这一区域图形更为平坦。

在很多时候，参数平原的提示是对的 -- 因为我们选择的参数，其实价格变化的函数；但它毕竟不是价格变化。最直接的方法是，当价格发生轻微变化时，策略的性能如果仍然处在一个平坦的表面，就更能说明策略是鲁棒的。

不过，这种图很难绘制，所以，Build Alpha绘制的仍然是以参数为n维空间的坐标、策略性能为其取值的三维图，但它不再是基于单个历史数据，而是基于一组历史数据：真实历史数据和增加了噪声的数据。