改用十进制!点差如何影响策略
Table of Content
笔记左数效应、整数关口与光折射中引用了南加州大学Lawrence Harris的一篇论文中,哈理斯研究了交易价格的聚类效应。聚类效应对我们确定压力位、完善下单算法都有一定的影响。
但是,2001年,美股变更交易制度,由分数制切换为十进制。这个变化就导致了他的研究结论作废。
这也是我们在量化中必须要注意的:你用来分析的数据,它是连续一致的吗?中间有没有任何制度上的、采集上的改变?如果有,我们还能不能把变化点前后的数据当成一个整体来研究使用?
这篇文章,就借这件事,介绍下美股历史上的分数制到十进制的切换,提醒大家在进行量化研究时,对数据源要进行认真分析。在世坤的《Finding Alpha》那本书中也讲过,寻找Alpha的过程中,可能最重要的是就是了解你拿到的数据。数据本身的缺陷,是产生各种偏差最常见又最难以发觉的原因。
美股历史上使用的最小增量单位(minimum spread,也称为tick size,点差)是1/16美元。这种规则有时候被称为fractions(分数制)。2001年4月起,点差改为十进制,即最小增量为$0.01。自2005年起,又推出了612规则,即对在$1之下的股票,允许它们以$0.0001的增量进行报价。
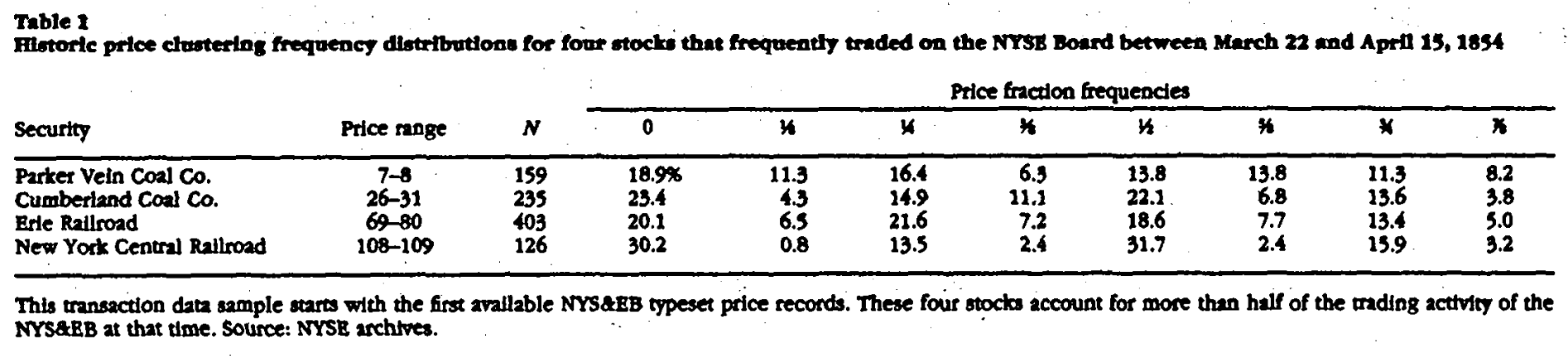
根据哈理斯等人在《Stock Price Clustering and Discretenss》中的研究,使用分数制点差时,股票价格更容易聚集在整数上,整数比一半(即8/16)更常见,一半则比1/4又更常见。比如,在1987年12月31日,CRSP(Center for research in security prices,芝大下属机构。这是研究美股的一个很重要的数据库,已经有55年历史了)每日股票数据库中,2510个收盘价中有2431个可以被l/8整除,整数点比17.3%,半数点12.8%。这一现象对下单策略的优化是十分重要的。此外,与十进制相比,它也显著地增加了做市商的利润。
当最小点差改为十进制,即最小单位变化为0.01美元时,这样一些事情发生了:首先,订单撮合时的时间优先的价值变低了。因为点差很小,所以交易者可以略微提高价格,从而优先成交。而在此之前,由于点差较大,想提高价格会导致利润发生较大的变化,从而宁愿保持价格不变,多排队一段时间。因此,十进制会稍稍增加一些交易量,因为成交更容易了。
在哈理斯的论文中还存在其它一些重要结论。显然,由于交易规则的修改,这些结论,特别是关于价格分布的结论,现在都已失效了。根据这些观察而编写的交易算法(特别是下单算法和做市商策略)也不得不修改。
此外,在使用分数制时,整数关口的压力和支撑更强(尽管1美元被划分成了16个档位,但交易者只倾向使用0,1, 4,8等等这样少数几个档位,因此在这些档位上聚集的委单更多,压力和支撑也就更强)。使用十进制之后,我们以$2的股票为例,从$2.0,$2.1,$2.2直到$2.9,每一档都是易记、易操作的整数位,因此聚类效应会减轻一些。
另外,性急的交易者也会使用$2.11来买进,或者$2.09来卖出,从而使得价格会适当分散一些。因此,十进制下整数关口的支撑和压力会相应地比fractions交易制下轻一些。如果我们的策略(因子)与整数关口相关,那么,数据是不应该跨过2001年4月这条分界线的。
在切换到十进制期间,何彦(新加坡管理大学)等人对切换带来的差异进行了研究,他们的论文《price rounding and bid-ask spreads before and after the decimalization》,发表在《经济与金融国际评论》期刊上。他们的结论是,转换为十进制后,价格往往集中在100、50、25、10和5美分上,做市商的利润有所下降。
但是两篇论文都比较学术化,并没有指出这种价格聚类在交易中的意义:
- 价格聚类形成密集成交区,从而构成压力和支撑位,分数制转向十进制后,形成了新的价格聚类点,也就是发生了压力位和支撑位的漂移。对应的因子策略需要进行修改。
- 下单算法需要针对这一现象进行优化
- 分数制转向十进制,可能导致之前的做市策略失效。
此外,在A股,我们发现价格聚类在10元以内,可能在每一个0.1元处都发生,而不是0.05,另外,指数则可能是以100为聚类点。如果我们要自己去探索这种规律,何彦等人的研究方法是可以借用的。
在A股,也有类似的事件。比如,A股在2005年前后进行了股权分置改革,进入了全流通时代。同一家公司,在改制前后,可以流通的股份发生了较大的变化。每股对应的基本权益也必然发生较大变化。
这里可以认为发生了一个基本面上的断裂层。因此,如果你要进行基本面分析,也许要先检视一下,数据在跨越2005年时,会不会有影响。
有的数据源在提供数据时,仅从2005年起开始提供,无论是否是出于这方面的考虑,但确实有它道理。