factors »

动能反转：二阶导动量因子年化Alpha达到61%！

Table of Content

这一期，我们将介绍一个二阶导因子。我们将演示二阶导因子的探索优化过程，进一步介绍因子分析的原理，包括：

如何让 Alphalens 使用我们指定的分层
二阶导动量因子的数学原理
By quantiles or By bins, 分层究竟意味着什么

最后，我们在 A 股 40%的抽样中，得到最近半年二阶导因子的最佳参数是 5 天。在此参数下，年化 Alpha 分别是 38.4%（多空）和61.5%（单边做多）， beta 为-0.12，即收益独立于市场。

这是在不同周期、多空组合条件下产生的收益情况：

条件	Alpha	Beta	累计收益
多空、2	30.6%	-0.06	15%
多空、4	35.3%	-0.1	17%
多空、5	38.4%	-0.12	19%
多空、6	37.3%	-0.12	18%
多空、8	32.4%	-0.06	14.8%
多空、10	23.2%	-0.07	11%
单多、10	17.6%	-0.60	15%
单多、5	61.5%	-0.58	37%

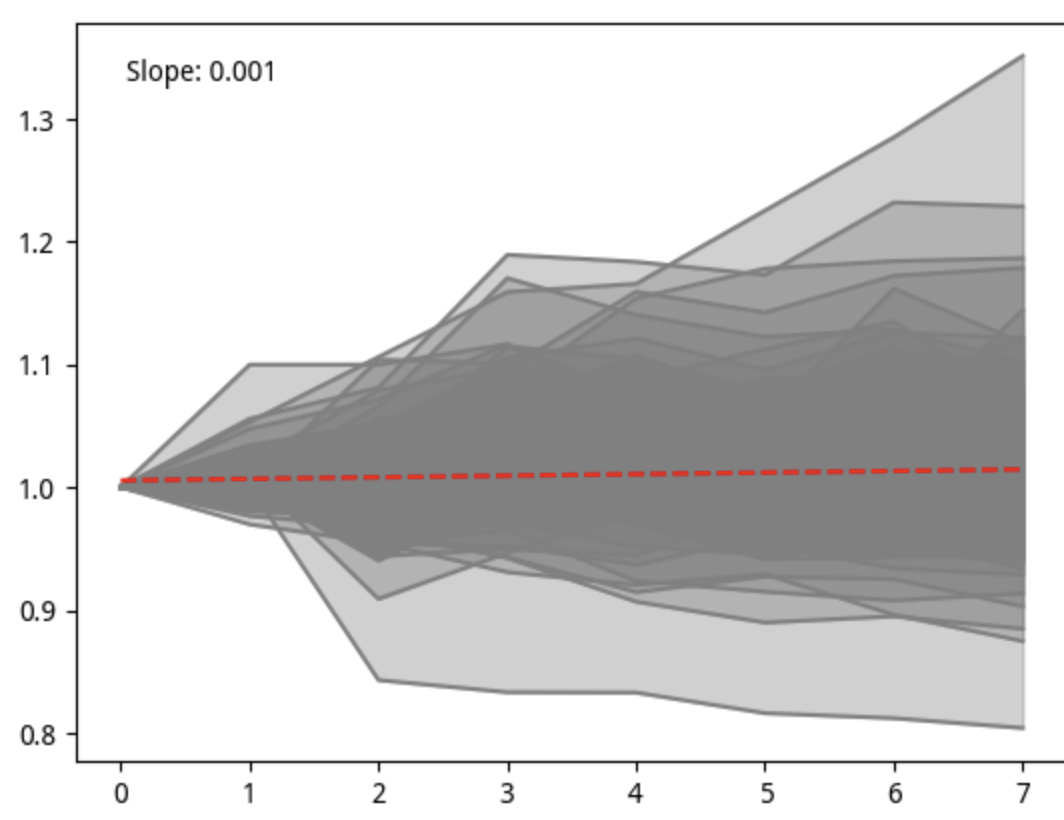
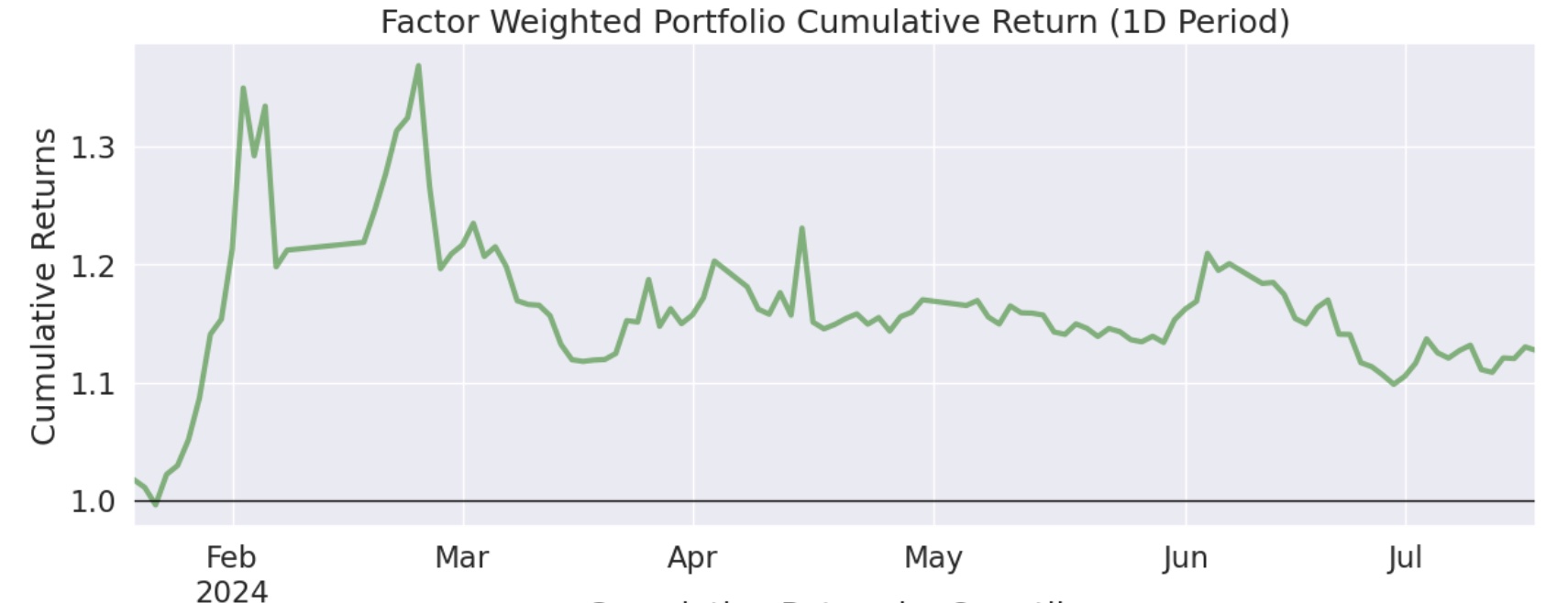
我们任意抽取一天选出的样本，绘制7天的走势平及样本均值的趋势线，验证因子分析结果可靠：

全部代码及数据购买本文后，私信留言，您将会收到一个在线网址和登录密码。这里有本文全部代码、A股2005年以来的行情数据（含分钟线）和回测引擎，支持在线运行和验证。

上一期我们检视了斜率因子。本质上，斜率因子是一阶导动量因子。比如，以如下方式生成的数组，它的斜率和一阶导是相等的：

from scipy.stats import linregress

slope = 0.2
x = np.arange(10)
y = slope * x + 1

d1 = np.diff(y).mean()

# 如果我们通过线性回归来求斜率
alpha, beta, *_ = linregress(x, y)

print(f"slope is {slope:.1f}")
print(f"first derivative is {d1:.1f}")
print(f"slope by linear regression is {alpha:.1f}")

三项输出都是 0.2。如果我们对价格序列求二阶导作为因子，它会对未来趋势有预测作用吗？我们先看结果，再来讨论背后的原理。

二阶导动量因子检验¶

def d2_factor(close: NDArray, win: int = 10) -> NDArray:
    n = len(close)

    d1 = close[1:]/close[:-1] - 1
    d2 = d1[1:] - d1[:-1]

    factor = move_mean(d2, win)
    # 进行左填充，使之与输入等长
    factor = np.pad(factor, (n-len(factor), 0), ...)

    return factor

上面这段代码可以生成一个二阶导动量因子。注意我们用close[1:]/close[:-1]-1代替了通常意义上的一阶导，以起到某种标准化的作用。如果我们不这样做，那么高价股的因子将永远大于低价股的因子，从而永远有更高的因子暴露。

因子本身的参数是win，表示我们是在多长的时间段内计算的二阶导。

然后我们通过 Alphalens 来进行因子检验。第一次调用 Alphalens，我们按 quantiles 分层，分层数为 10。

从分层图来看，继续进行收益分析是没有意义的，我们必须先进行优化。

第一次调优¶

考虑到做多收益在第 9 层达到最大值，所以，我们考虑 drop 掉第 10 层后进行分析，看看结果如何。

通过 Alphalens 进行分析中，一般有三个步骤：

构造因子。
数据预处理，一般是通过调用 get_clean_factor_and_forward_returns 来实现的。
调用 create_full_tearsheet 来执行因子检验并输出报表。它的输入是第 2 步中的输出。

Alphalens 是在第二步实现的分层。然后它将第二步的输出，用作第 3 步的输入。

所以，我们可以在拿到第 2 步的输出之后，drop 掉第 10 层，然后调用 create_full_tearsheet 来进行收益分析。这样，在 Alphalens 看来，top 分层就是第 9 层，所有的分析都是在这个基础上进行。

根据 Alphalens 的官方文档，这样做是允许的。

第 2 步输出的是一个 DataFrame，它的格式如下：

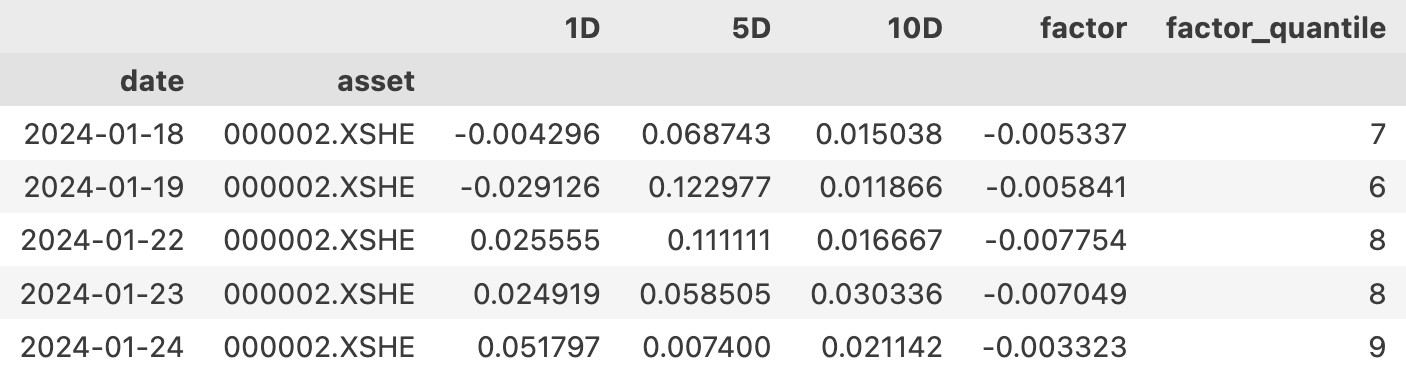
所以，要 drop 掉第 10 层，可以这样做：

factor_data = factor_data[factor_data.factor_quantile <= 8]

Tip

这是本文介绍的第一个技巧。在前面的课程中，为了让 Alphalens 按照我们的意愿，按指定的对空分层进行收益分析，我们使用的是改造因子本身的方法，比这个方法在阶段上更提前一些。两个方法都可以使用，但这里的方法更简单。

这一次我们得到了令人满意的分层收益均值图，单调且递增，完全适合进一步进行因子分析。

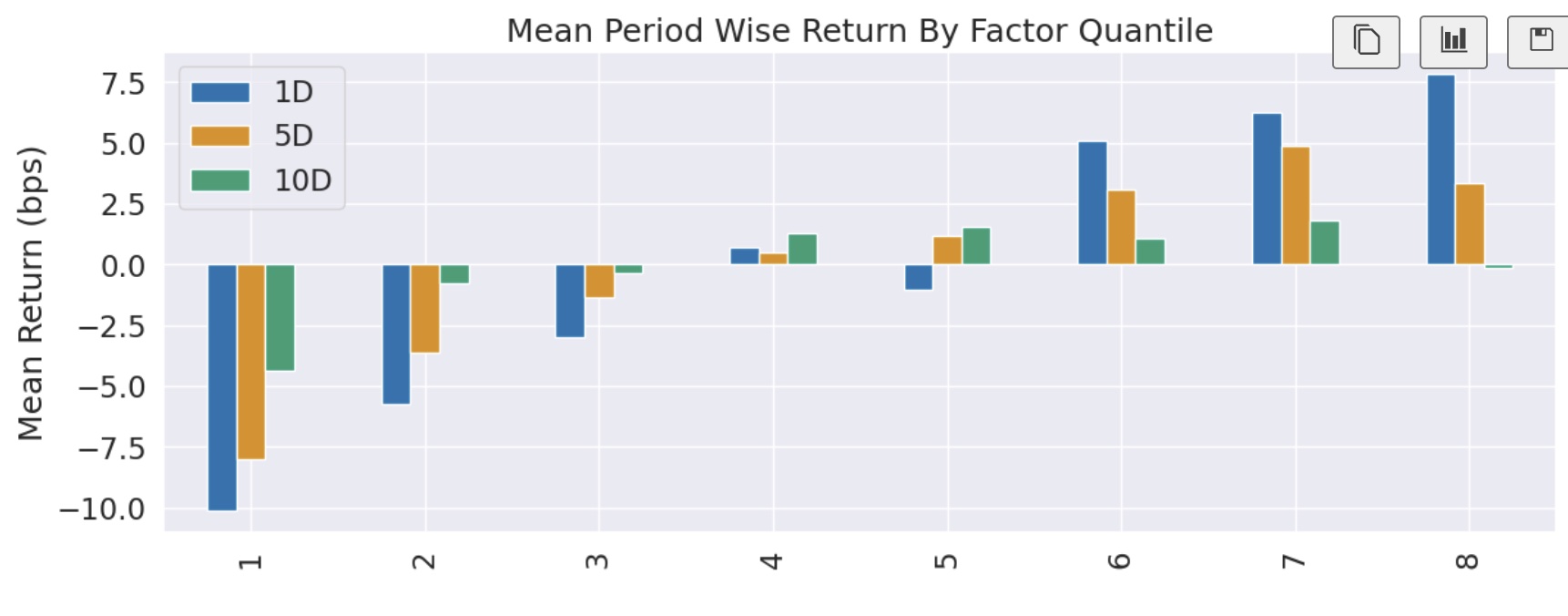
这个图其实基本上就是完全还原了上一个图，只不过缺少第 10 层而已。但是，现在第 9 层就成了 top 分层，这是 Alphalens 在计算多空收益时，将要做多的一层。

Tip

由于我们在实盘交易中也一样可以 drop 掉第 10 层，因此这种操作是合理的。类似的手法，我们在 Alpha101 中也可以看到。

现在我们得到的 Alpha 是 23.2%（1D 年化），Beta 是-0.07，7 个月的累计收益是 11%左右。

纯多的情况¶

我们在之前的几期里讲过，由于制度因素，并不是所有人都能条件做空。所以我们看看纯做多的情况下，因子表现如何。

这一次，年化 Alpha 只有 17.6%，beta 为-0.6。但 7 个月的累积收益是 15%左右，还略高了一些。

条件	Alpha	Beta	累计收益
多空、10	23.2%	-0.07	11%
单多、10	17.6%	-0.60	15%

我们对比一下前后两次的累积收益图，可以发现，多空组合绝对收益低了一些，但平抑风险的能力更强了：

多空组合

单边做多

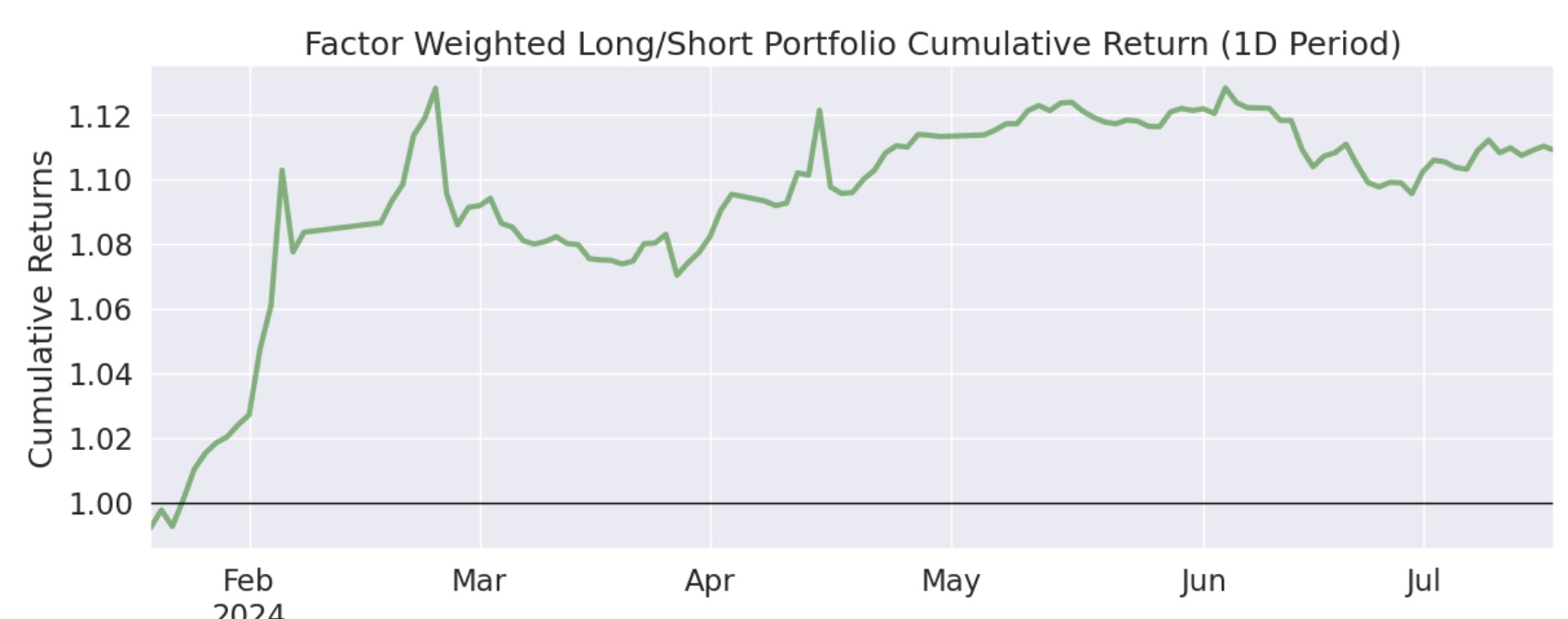
为什么多空的 Alpha 大于纯多，多空组合的累积收益还低于单边做多？这可能是在对二阶导因子做空的过程中，有一些负面效应。一些强势股，在急杀之后（二阶导为负），往往还会有一个小反弹，如果刚好在小反弹前做空，就会带来损失。

寻找最有效的窗口¶

到目前为止，我们使用的都是 10 天的窗口来计算的二阶导。如果使用其它窗口呢？我们分别测试了 2、4、6、8 天的数据。现在，我们把所有的数据汇总起来：

条件	Alpha	Beta	累计收益
多空、2	30.6%	-0.06	15%
多空、4	35.3%	-0.1	17%
多空、5	38.4%	-0.12	19%
多空、6	37.3%	-0.12	18%
多空、8	32.4%	-0.06	14.8%
多空、10	23.2%	-0.07	11%
单多、10	17.6%	-0.60	15%
单多、5	61.5%	-0.58	37%

看起来在 A 股市场上，二阶导动量因子使用周期为 5 时表现最好。此时如果能构建多空组合，年化 Alpha 是 38.4%，今年以来累计收益是 19%；如果只能构建单多组合，年化 Alpha 是 61.5%，今年以来累计收益是 37%。

回顾一点高中数学¶

前一期讨论的斜率因子（即一阶导因子）反映的是价格上涨的速度。

那么二阶导因子代表什么呢？

二阶导因子反映的是价格变化的加速度。当一阶导为正，而二阶导为负时，价格将仍然上涨，但趋势减缓，有可能出现变盘。反之亦然。下面的公式显示了一个存在二阶导的函数：

\[ y = a x^2 + b x + c \]

当 a 和 b 分别在 [-1, 0, 0, 1] 和 [10, 10, -10, -10] 之间取值时，我们就得到下面的图形：

50%

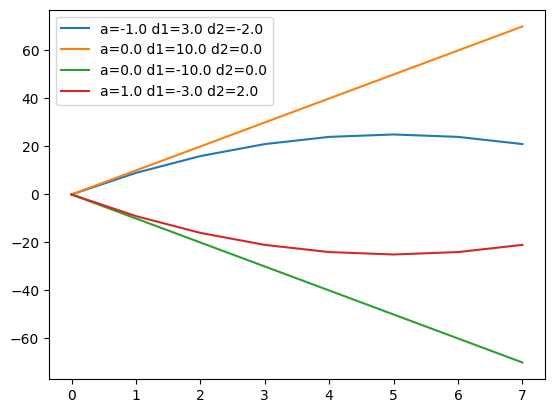
这个图说明，二阶导对证券价格运行的趋势具有修正效应。本来处于上涨趋势的品种，如果二阶导持续为负，它迟早会到达峰顶、然后转为下跌；反之，本来处于下跌趋势的品种，如果二阶导持续为正，它迟早会触及谷底，然后转为上涨。

正因为这样，与一阶导不同，二阶导有能力提前预测价格趋势的变化。它是一种反转动能。

在测试中，表现最好的参数是 5 天。考虑到二阶导需要额外多两个窗口才能计算，因此我们实际上是基于过去 7 天的数据来发出交易信号。

7 天，这是上帝之数。

眼见为实¶

看到 38%的 Alpha，老实说有点吃惊。

这是真的吗？还是说什么地方 Pseudo-Logoi，这位谎言之神悄悄地溜了进来？

尽管可以相信 Alphalens 是品质的保证，但比起一堆统计数字，你可能更愿意相信自己的卡姿兰大眼睛。

所以，我决定把第 9 层的个股走势画出来。绘制方法是，先取出某一天（记为 T0）quantile = 9 的所有标的，然后再取出最近 9 天（截止 T0 为止）的收盘价。在绘图之前，先对收盘价起点归一化到 1。

绘图中，我们共使用了199个样本，代表性和稳健性都足够了。

图中的红色线是趋势线，其斜率是 0.001，表明总体上是上涨的；颜色的深浅，代表了样本的分布密度，可以看出，零线上方分布更多一些。

我很喜欢从一些股谚中寻找灵感。因为公司底色、市场机制和交易制度的不同，照搬海外股市的做法是行不通的。我们这边博弈的底色更重一点。

按理说，跟二阶导动量因子有关的股谚是黄金坑和圆弧顶，或者 V 反。那么，能直观地画出来在这些标的中，有多少漂亮的黄金坑吗？

很难只用一张图、同一个参数就绘制出来：每个黄金坑的周期、深度和构造阶段等指标都是不一样的。环肥燕瘦，我们很难一笔画尽美人风姿。

By bins, or By quantiles？¶

在这次测试中，我们一直使用的都是 by quantiles 进行的分层，没有探索 by bins 分层。

by quantiles 是一种排名分层。这是 quantiles 的定义决定的。使用 by bins 方法，我们更关注的是因子值本身的金融含义。

比如，对 RSI 来说，它的值在 0 到 100 之间，大家会认为超过 80 的值是“超买”，低于 20 的值是“超卖”。因此，直接使用因子值是有意义的。

本文没有使用 by quantiles 方法，一方面因子值本身的信号意义可能没那么强：

我们寻找买入或者卖出信号，是根据后面是涨还是跌来验证的。但是，二阶导只能告诉我们趋势的改变方向，并不能立即决定涨跌。

因此，我们可能更应该使用它的排名来做因子，因为资金往往会寻找反转动能最强的标的。

Info

题外话：by quantiles 分层用的是排名，有点 Rank IC 的感觉，但计算收益时，又是根据因子值来进行权重分配的，则与 Ranked IC 的方法区别。

通过这些参数以及它们之间的混搭，Alphalens 赋予了我们强大的探索能力。

另一方面，我并不清楚它的最小值、最大值和分布情况，所以在实操上难以给出bins数组。这也是没有使用 by bins 的原因。

当然，这并非绝对。也许，有时间的话，也应该探索下 by bins 分层。