factor&strategy »

拯救CCI！因子纯化后，证实CCI确实是超有效的技术指标！

#factor   #技术指标  

---

Table of Content

CCI（商品通道指数） 由 Donald Lambert 研发，首次发表于 1980 年的《商品期货》杂志，一直以来很受交易大量推崇。但是，简单地将这个指标作为因子进行因子检验，差点使明珠蒙尘。最后，因子密度分布图揭示了真相，通过因子纯化，最终检验结果给出了与传统经验一致的结论！

CCI的计算公式是：

\[ CCI=\frac{Typical Price - MA}{.015 * Mean Deviation} \]

其中，

\[ \text{Typical Price}_t=(H_t+L_t+C_t)\div 3 \\ MA = Moving Average \\ Moving Average = (\sum_{i=1}^PTypical Price)\div P \\ Mean Deviation = (\sum_{i=1}^P|Typical Price - MA|)\div P \]

简单来说，CCI 表示了价格对移动平均线的徧离程度。

Tip

MACD, PPO, CCI 和 BIAS 是一组非常相似的指标，它们的区别主要在于选择的价格序列不同，是否进行了归一化。在本章我们不会介绍 BIAS 指标，这里就顺带提一下。它的公式是：

\[ \text{Bias} = \frac{\text{当前价格} - \text{N 日移动平均线}}{\text{N 日移动平均线}} \times 100 \]

这个对比给我们提示了创新因子的一个思路。

CCI 使用最高价、最低价和收盘价的平均值作为价格序列的想法，在很多地方都很常见。本质上，它是对 vwap 的一种近似。因此，在有 vwap 数据可用的前提下，直接使用 vwap 数据有可能更好，后者的博弈含义更明确。

CCI 公式当中有一个魔术数字：0.15. 它的作用是为了使 CCI 的值标准化到一个合理的范围，并且能在-100和100边界处有信号意义。起初，公式的设计者 lambert 认为，当 CCI 在[-100,100]区间内时，意味着价格在随机波动，是不值得交易的。而只有当 CCI 绝对值超过了 100 时，才认为有趋势出现，即当 CCI 上穿 100 时买入，下穿-100 时卖出。

我们先用一个简单的双轴图观察一下这个指标。

df = PAYH.copy()
df['cci'] = ta.CCI(df.high, df.low, df.close, 14)

axes = df[['close', 'cci']].plot(figsize=(14, 7), 
                            subplots=True, 
                            title=['PAYH', 'cci'])
axes[1].set_xlabel('')
sns.despine()
plt.tight_layout()

这是输出结果：

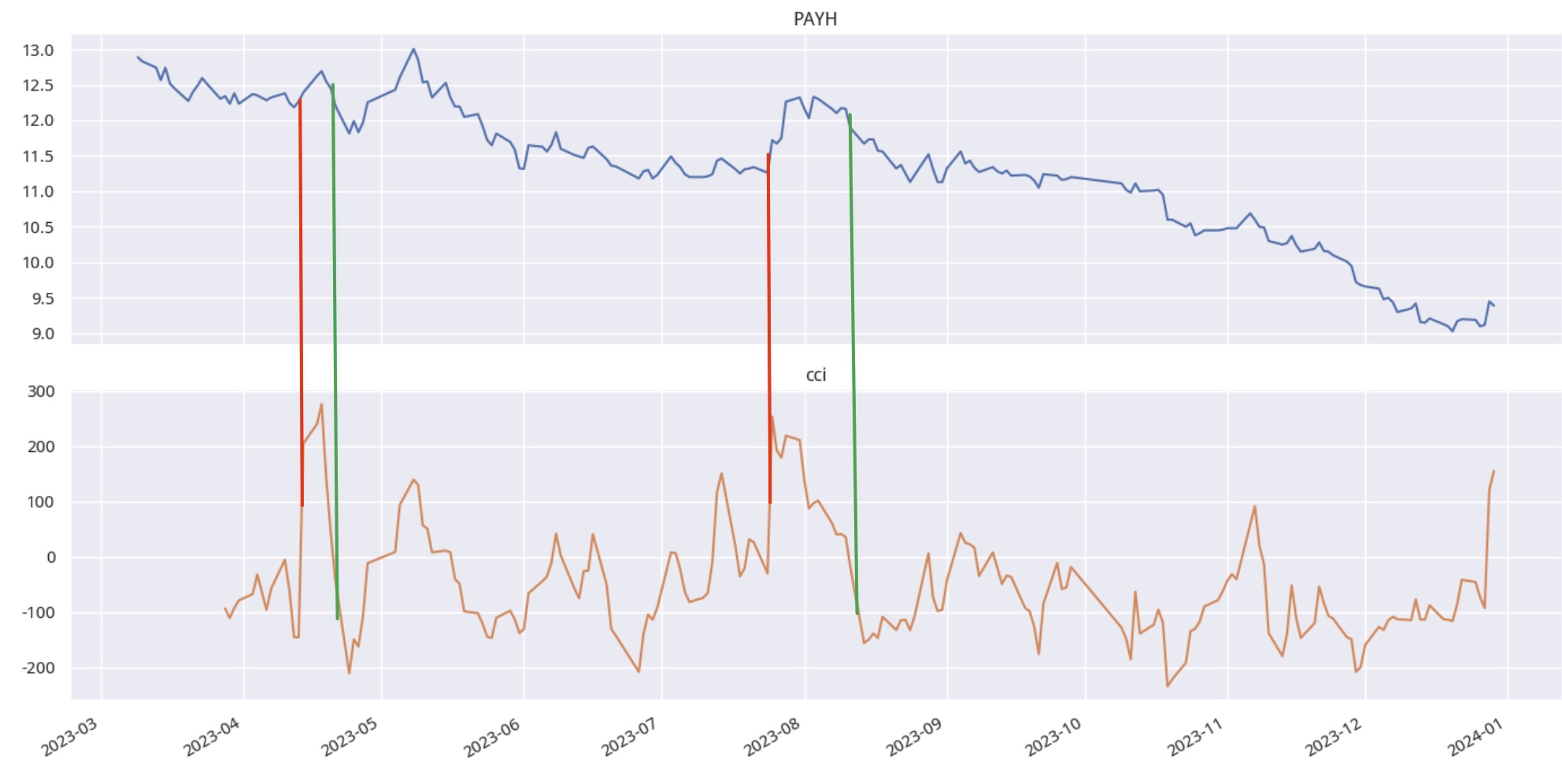
输出结果中，我在两处CCI穿越 \(\pm 100\) 的位置上标注了交易信号，以说明CCI的信号作用。这只是单个资产、某小段时间上的观察结果，说明不了问题。

现在我们运行因子检验来测试一下：

_ = alphatest(2000, start, end, 
              calc_factor = lambda x: ta.CCI(x.high, 
                                             x.low, 
                                             x.close, 
                                             14))

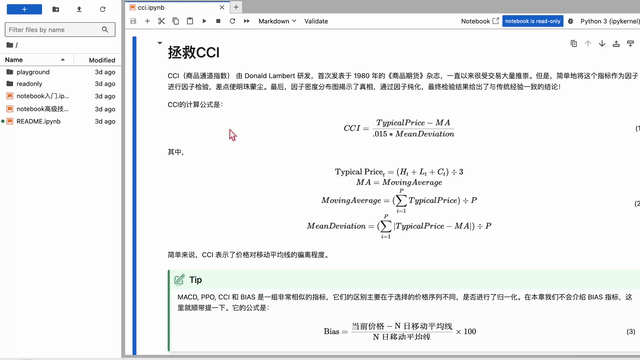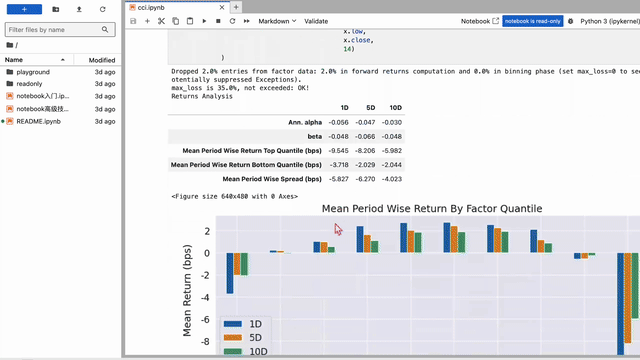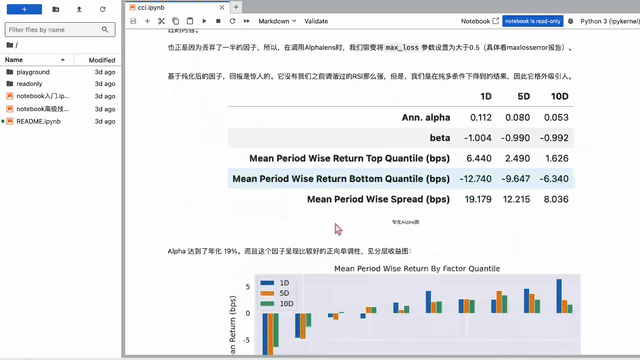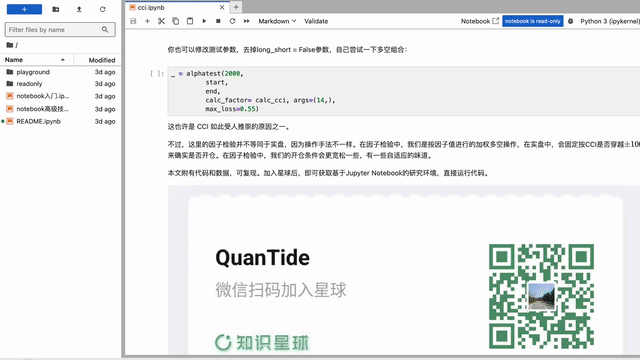
看起来因子测试的结果不是很好。

但是，只要对 CCI 的原理略加分析，我们就很容易明白，它不适合直接当成因子来使用。因为CCI的交易信号是，当CCI穿越\(\pm 100\) 时，就发出交易信号。它是一种事件信号，并不是我们通常意义上的因子。

下面，我们从因子分布的角度来讲一下为什么。

cci = barss.groupby(level="asset")
            .apply(lambda x: ta.CCI(x.high, 
                                    x.low, 
                                    x.close, 
                                    timeperiod=14
                                    )
                )

with sns.axes_style('white'):
    sns.distplot(cci)
    sns.despine()

从密度分布图来看，因子分布出现了双峰。

我们在课程中讲过，如果因子的分布出现双峰，这个因子往往包含了多种因素，它是不纯粹的。现在，我们面临的正是这种情况。在这种情况下，进行因子分析，我们需要先对因子进行“纯化”。

cci = barss.groupby(level="asset")
            .apply(lambda x: ta.CCI(x.high, 
                                    x.low, 
                                    x.close, 
                                    timeperiod=14))
with sns.axes_style('white'):
    sns.distplot(cci[cci> 0])
    sns.despine()

输出结果如下：

现在，我们看到的 cci 的分布就是单峰的了。然后我们对它进行因子检验，看看结果如何：

def calc_cci(df, n):
    cci = ta.CCI(df.high, df.low, df.close, n)
    cci[cci < 0] = np.nan
    return cci * -1

alphatest(2000, 
         start, 
         end, 
         calc_factor= calc_cci, args=(14,), 
         max_loss=0.55, long_short=False)

注意，这段代码的第三行，我们对返回前的CCI 进行了修正，使其负值部分被置为nan，从而它们将会在因子检验中被抛弃掉。这是之前讲Alphalens框架时讲过的内容。

也正是因为丢弃了一半的因子，所以，在调用Alphalens时，我们需要将max_loss参数设置为大于0.5（具体看maxlosserror报告）。

基于纯化后的因子，回报是惊人的。它没有我们之前调谐过的RSI那么强，但是，我们是在纯多条件下得到的结果，因此它格外吸引人。

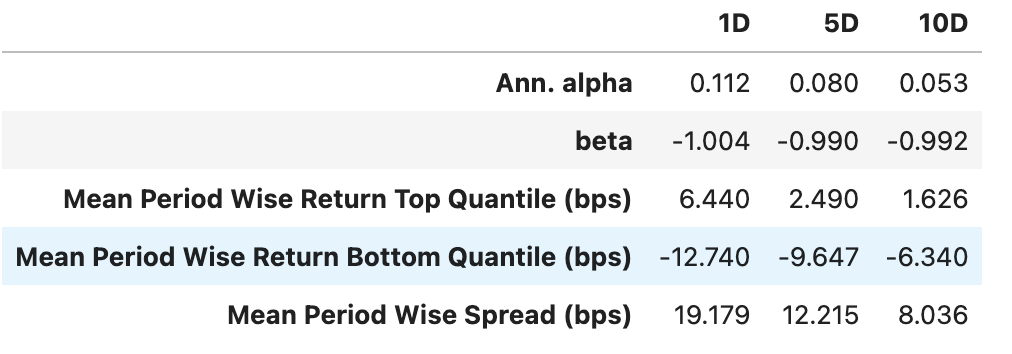
Alpha 达到了年化 19%。而且这个因子呈现比较好的正向单调性，见分层收益图：

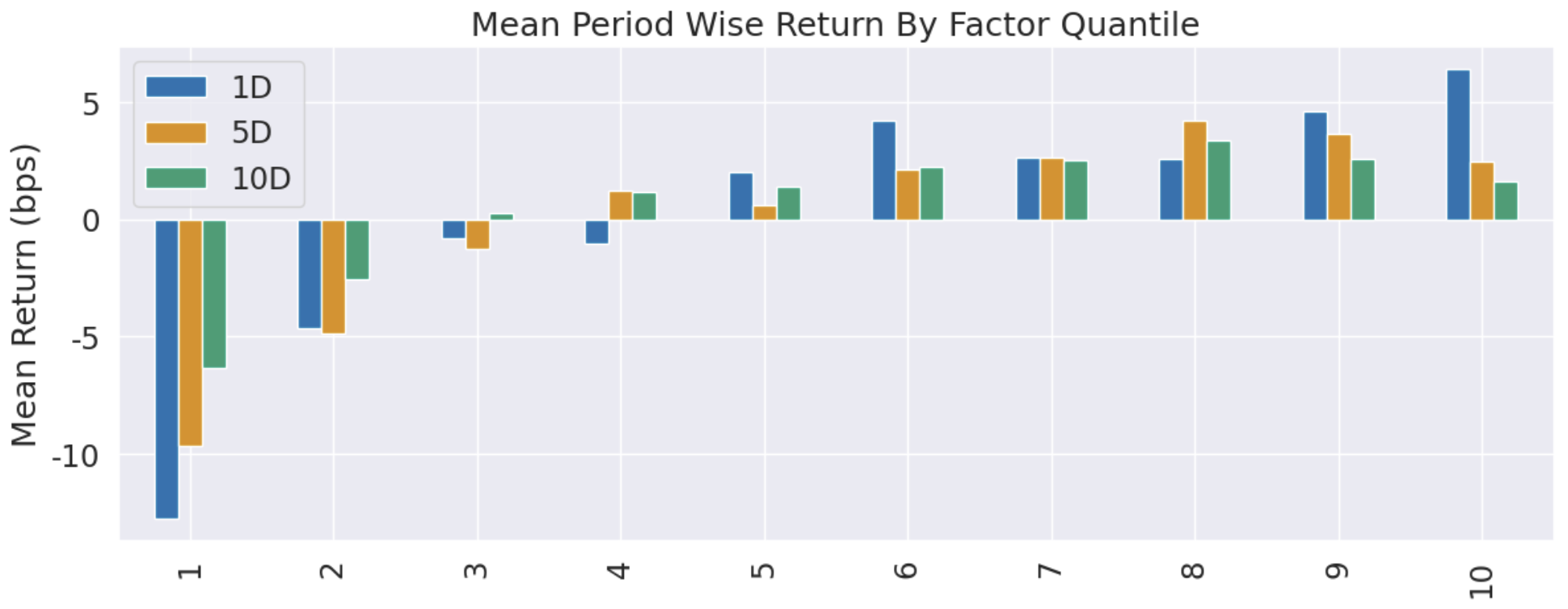
不过，它在纯多的情况下，累计收益表现不是很稳定。这一点也从前面的年化收益图中的beta值可以看出来，受市场波动影响比较大。

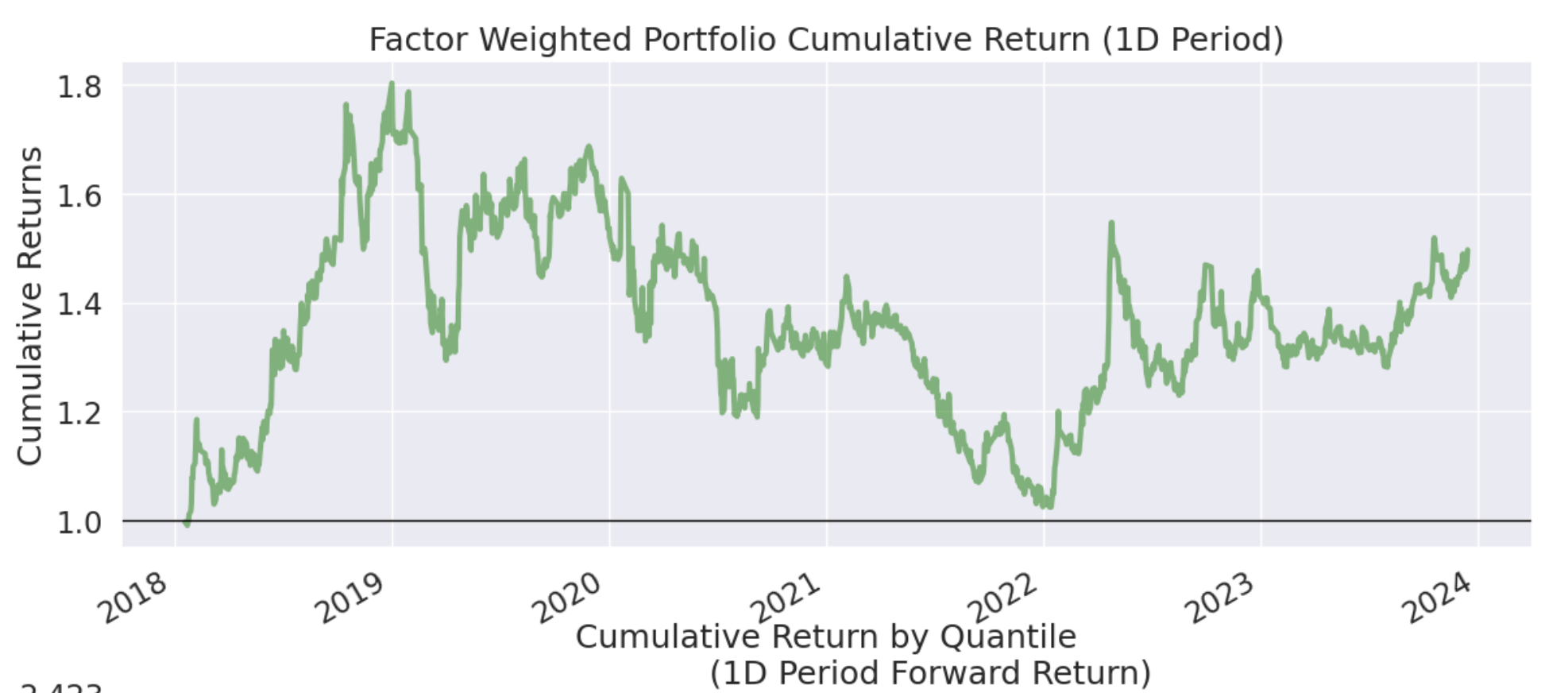
但是我们不一定非要纯多，本来CCI就是期货指标。我们来看看多空组合的情况：

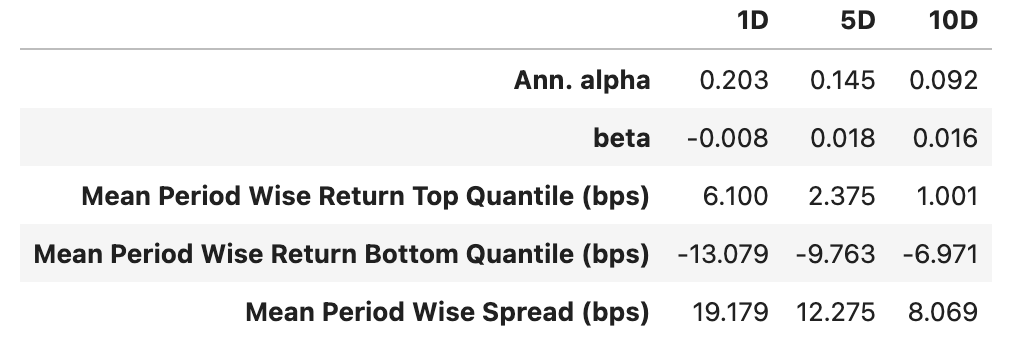
不仅Alpha收益很强，而且beta被对冲到几乎没有！在beta为零的情况下，累积收益就应该是平稳向上、且波动很小，我们来看看是否是这样：

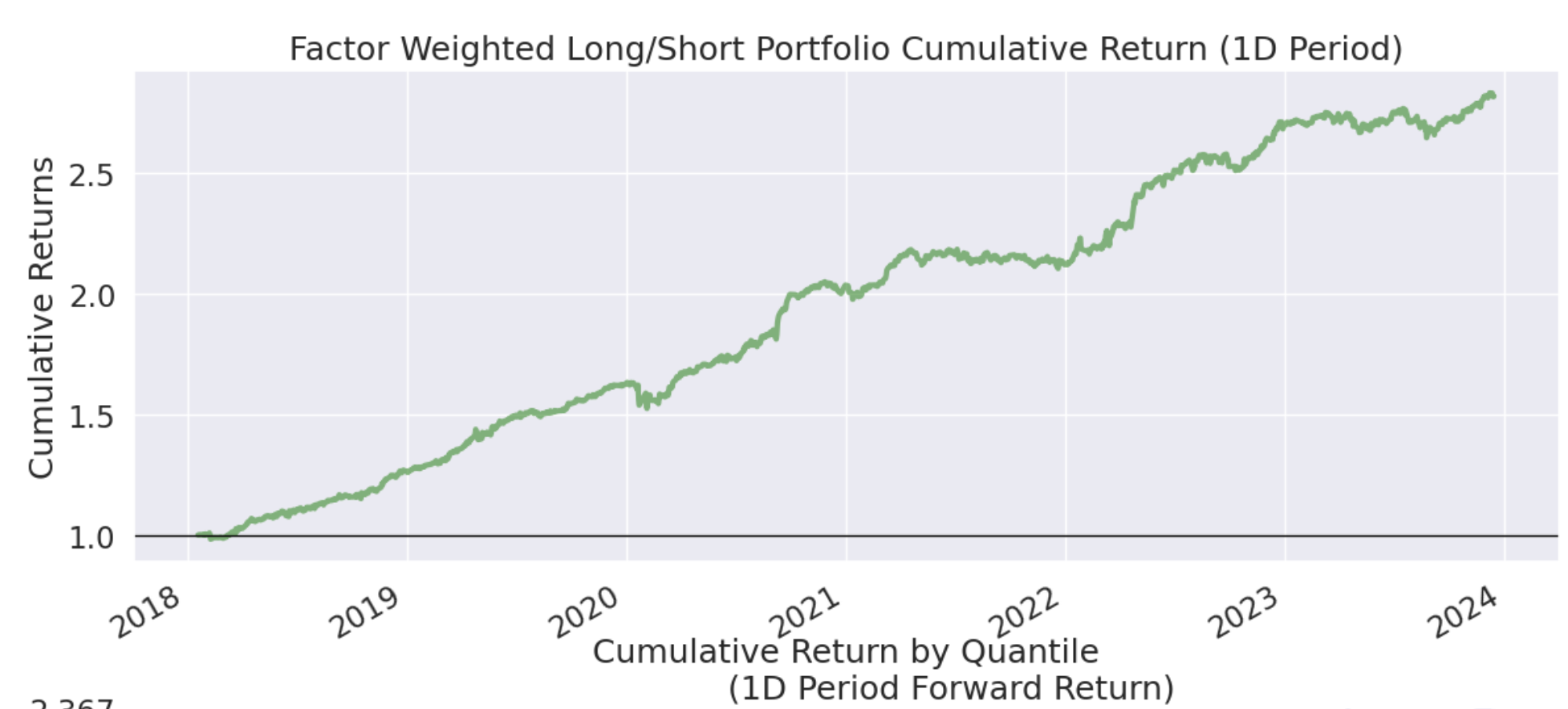
这也许是 CCI 如此受人推崇的原因之一。

不过，这里的因子检验并不等同于实盘，因为操作手法不一样。在因子检验中，我们是按因子值进行的加权多空操作，在实盘中，会固定按CCI是否穿越\(\pm 100\)来确实是否开仓。在因子检验中，我们的开仓条件会更宽松一些，有一些自适应的味道。

本文附有代码和数据，可复现。加入星球后，即可获取基于Jupyter Notebook的研究环境，直接运行代码。

在该环境中，除本文代码外，之前付费文章的代码也都在。并且，今后的文章只要声明附有代码和数据，可复现的，都能在此环境中找到。