algo »

PDF is all you need(3)

#pdf #algo #概率

Table of Content

在上一篇中，我们提到了二项分布，并且指出：

Tip

\[ P(X=k) = C_{(n,k)} \times p^k \times (1-p)^{n-k} \]

二项分布究竟意味着什么呢？实际上，有一个名为 Galton Board 的装置，可以很好地可视化它的含义：

图1 高尔顿板

Info

Galton Board 由英国科学家弗朗西斯・高尔顿设计。他是达尔文的表亲。他证明了每个人的指纹是独一无二的，且在人的一生中稳定。他还创造了优生学这个词，这个词在今天非常有争议。

具体来说，高尔顿板是一块竖直木板，顶部有一个小球入口，下方有等距的垂直隔板，形成多个凹槽；木板中间钉满了等间距的钉子，呈三角形排列（每一层钉子比上一层多一个，且与上层钉子错开，呈 Pascal 三角或者杨辉三角分布）。

当我们把小球从入口扔进木板时，小球会碰到中间的钉子，然后会向左或者向右弹开，直到碰到下一个钉子或者掉落到下方的垂直隔板。通过每个凹槽里落入的小球数量与小球总数之比，我们就可以知道小球在 n 次碰撞中，连续 k 次选择『右』或者『左』的概率。

实际上，Galton Board 装置的下半部分，正好就是我们在统计学中，常常会用到的直方图。凹槽的宽度可视为 “组距”，凹槽的高度（小球堆积的高度）则对应 “频率”。只不过，在绘制直方图时，我们可以任意指定组距。

在这样一个装置中，如果钉子数越来越多，试验次数也越来越多，会发生什么情况呢？下图显示了在有20层钉子，试验500次时的一种可能结果：

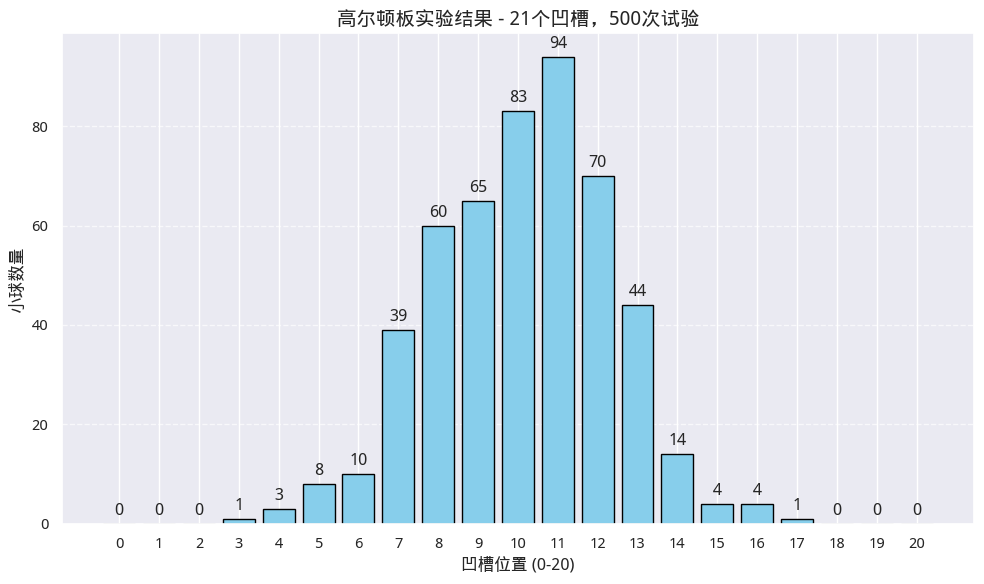图2 碰了1万次钉子，得到这个结果！

Tip

要模拟这个试验，我们需要使用 numpy.random 中的 binomial 函数。它能高效模拟一系列独立的伯努利试验。

```python

from numpy.random import binomial, histogram right_turns = binomial(n=layers, p=0.5, size=balls) counts, _ = histogram(right_turns, bins=np.arange(layers + 2))

在这个图中，如果我们把每一个凹槽按位置进行编号，把小球落入的位置看成事件的取值，那么我们就得到了一个离散型的随机变量。在图2中，它的取值区间是[0, 20]。

如果我们增加层数，多试验几次，又会如何？下图显示了1000个凹槽、1百万次试验的一种可能结果：

<div style='width:66%;text-align:center;margin: 0 auto 1rem'>
<img src='https://cdn.jsdelivr.net/gh/zillionare/imgbed2@main/images/2025/08/20250807160423.png'>
<span style='font-size:0.8em;display:inline-block;width:100%;text-align:center;color:grey'>图3 频率/随机变量图</span>
</div>

我们看到随机变量的中心值是500左右 -- 说明我们的实验是正确的，因为凹槽的个数是1000。但最小值与最大值并不是0和1000，这是因为我们试验的次数还不够多，要使得二项分布取到这样的极限值还是非常困难的。但是，如果凹槽的个数只有10个，而试验次数达到1000次，就很容易取到（0， 10）这两个极值了。

或许你已经注意到，这次的图跟图2有一点不一样。这次我们绘制的实际上不再是直方图，而是概率密度/随机变量图。我们用来绘制这张图的代码是：

```python
import matplotlib.pyplot as plt

plt.hist(positions, bins=num_grooves, density=True)

这里的关键参数是 density=True。当指定它为 True 时，直方图绘制函数 hist 绘制的 y 轴就不再是每一个箱的频数，而是概率密度。

这个概率密度是这样算的。在图3中，我们要求把落在大致范围(428, 575)内的随机数，按1000个分箱进行平均分组，这样得到组距大约在0.147的箱子共1000个。每个箱子里落到的随机数（小球个数），计作\(X_i\)，则\(\frac{X_i}{n \times 0.147}\) 就是 \(X\) 在这个分箱中的概率密度。按几何概率的求法，这个概率密度乘以分箱长度 -- 即小矩形的面积 -- 就得到了小球落在该区间的概率。

Question

现在，我们思考一个问题，如果将这1000个矩形求面积，再加起来，我们将得到多少？

显然，这1000个矩形的面积之和应该等于1。因为它就是所有事件发生的概率之和。如果我们问，随机变量 X 小于500的概率是多少？那就是把从左到右，前500个矩形的面积加起来。

如果我们继续扩大凹槽数量和试验次数，比如说凹槽增加到1万个呢？最终，每个分箱和它们对应的概率密度在图上会紧挨在一起，从而在视觉上无法将其分开，我们将得到下面的图：

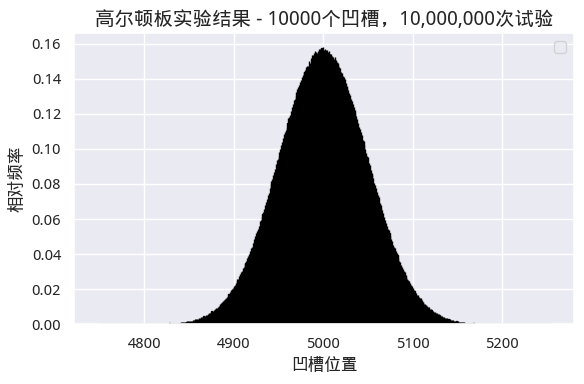图4 趋近于正态分布

但是，这张图仍然是由若干个矩形组成的。对于任意一个\(X_i\)，我们都能通过计算前\(i\)个矩形的面积和，来算出\(X \ge X_i\)的概率。尽管矩形个数增加了，但所有的小矩形的面积和仍然为1。

如果我们继续加大钉子的层数和试验次数，使得它们都趋向于\(+\infty\)呢？这时候，不仅仅是矩形从屏幕上消失，它们实际上在物理意义上也不构成矩形了。这时候我们只会看到屏幕上一条平滑的钟形曲线。

在这个趋向于无穷大的过程中，会发生什么呢？在 Galton Board 中，随机变量的取值（小球能落入的凹槽位置）是有限的，是离散值。而当 \(n\) 和钉子层数（实际上也就是凹槽个数）趋向于无穷大时，随机变量的取值也将由离散值变为连续值。

现在，再来求事件\(X \ge X_i\)的概率，我们就无法通过小矩形的面积和来计算了。不过，当小矩形的长度趋近于零时，求和正好是积分的含义。于是，我们就得到积分表示的分布函数。

PDF 和 CDF¶

在前面的讨论中，我们已经接触到了 PDF （Probability Density Function）和 CDF（Cumulative Distribution Function）。前者被翻译成为概率密度函数，后者被翻译成为累积分布函数，常常也被简称为分布函数。

Tip

现在，我们也许可以理解 plt.hist 方法中的 density 参数的含义了。它表明我们要求 y 轴的值是概率密度，而不是频数。

显然，从前面的介绍中，我们发现，CDF 是 PDF 的积分，那么 PDF 就是 CDF 的导数。我们有以下公式：

\[ F(x) = P(X\le x) = \int_{-\infty}^{x} f(t) dt \tag {CDF} \]

\[ f(x) = F'(x) \tag {PDF} \]

\[ P(X_a \leq x < X_b) = \int_{a}^{b} f(t) dt \tag {X 落在 a 到 b 的概率} \]

因此，PDF 是 CDF 的一阶导数，反映了 CDF 在某点的变化率。而 CDF 是指随机变量的取值小于或等于 \(x\) 的概率。

为了理解 CDF 与 PDF 的计算，我们举一个简单的例子，均匀分布的概率密度函数。

假设随机变量 X 在区间\([0,n]\)上均匀分布，则概率密度为\(f(x) = \frac{1}{n}\)，概率分布函数为\(F(x) = \frac{x}{n}\)。

此时，要求随机变量 X 落在区间 a,b 上的概率是：

\[ \begin{align} \int_a^b\frac{1}{n}dx = \frac{b-a}{n} \end{align} \]

为了帮助大家理解，作为量化人，这里举一个量化场景下的例子。这个例子在『量化24课』中详细讲解过。

!!! question 已知某天上证指数已下跌4%，问此时抄底，成功能的可能性是多少？我们可以把上证指数的涨跌幅看成是一个随机变量。假设我们已知它的概率密度函数是\(f(x)\)；当已经下跌4%时，继续下跌的概率即是要求随机变量取值小于或者等于 x （此时为-0.04）的概率，也即 \(\(p = \int_{-\infty}^{-0.04} f(x) dx\)\) 已知继续下跌的概率为\(p\)，那么\(1-p\)就是抄底成功的概率。

概率密度函数只适用于连续型随机变量。这当然是对的，因为 PDF 与 CDF 之间是积分与导数的关系，所以，PDF 概念对离散型随机变量自然就不适用了。

期望¶

上一期『PDF is all you need』发表之后，有同学问，可不可以讲一点博彩概率（大意是这样？）。我对这些名词都不太懂。不过，大致上应该是跟期望有关的东西。

因为在博弈中，期望（Expected Value）是分析策略选择、评估局势优劣的核心工具，尤其适用于存在不确定性（如对手策略、随机结果）的博弈场景。其核心逻辑是：通过计算不同策略的期望收益（或损失），选择能最大化自身利益（或最小化风险）的最优策略。

期望（又称均值）是随机变量取值的加权平均值，权重是每个取值对应的概率。

期望一般用符号 \(E(x)\) 来表示。X 是随机变量。如果 X 是离散的，那么期望是“每种结果的取值 × 该结果发生的概率”之和，即：

\[ E_x = \sum_{i}^{n}X_{i}.P_i \]

这里\(X_i\)是第\(i\)种结果，\(P_i\)是对应的概率。

对于连续情况，期望的求法要难懂不少。由于对于\(X_i\)，不存在对应的概率，只有对应的概率密度，因此期望要通过积分来计算，即：

\[ E(X) = \int_{-\infty}^{+\infty} x \cdot f(x) \, dx \]

它可以理解成为概率密度函数（PDF）曲线与坐标轴转成的『加权面积』，本质上，相当于计算一个特殊图形的质心。

我们可以通过下面的代码，把『加权面积』和『重心』都绘制出来。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 定义正态分布：均值=5，标准差=1
mu, sigma = 5, 1

# 定义 X，pdf, x·f(x)
x_norm = np.linspace(mu-3*sigma, mu+3*sigma, 1000)
y_norm_pdf = norm.pdf(x_norm, mu, sigma)
y_norm_g = x_norm * y_norm_pdf

mask = x_norm <= 6

plt.figure(figsize=(10, 8))

# 第一个子图：正态分布的PDF
plt.subplot(2, 1, 1)
plt.plot(x_norm, y_norm_pdf, 'b-', label=f'正态分布 N({mu}, {sigma}^2) 的PDF')
# 只填充到x=6的区域
plt.fill_between(x_norm[mask], y_norm_pdf[mask], alpha=0.3, color='blue')

# 计算第一个子图中到x=6的积分值（累积概率）
integral_pdf_up_to_6 = np.trapezoid(y_norm_pdf[mask], x_norm[mask])

# 计算子图1中，到 X=6 时的重心
area = np.trapezoid(y_norm_g[mask], x_norm[mask])
centroid = area / integral_pdf_up_to_6

# 标注积分值
plt.annotate(f'x=6时的累积概率: {integral_pdf_up_to_6:.2f}',
             xy=(6, 0), 
             xytext=(6-1.5, 0.3),
             arrowprops=dict(facecolor='black', shrink=0.05),
             fontsize=10,
             bbox=dict(facecolor='white', alpha=0.8))

# 绘制x=6的竖线
plt.axvline(6, color='purple', linestyle='--', label=f'x=6')
E = np.trapezoid(y_norm_g, x_norm)
plt.axvline(E, color='green', linestyle='-', label=f'期望= {E:.2f}')
plt.title('正态分布的PDF与到x=6的累积概率')
plt.legend()
plt.grid(alpha=0.3)

# 绘制 X < 6的图形的重心
plt.axvline(centroid, color='orange', linestyle='--', label=f'重心= {centroid:.2f}')
plt.annotate(f'x=6时的重心: {centroid:.2f}',
             xy=(centroid, 0), 
             xytext=(centroid-2, 0.2),
             arrowprops=dict(facecolor='black', shrink=0.05),
             fontsize=10,
             bbox=dict(facecolor='white', alpha=0.8))

# 第二个子图：g(x) = x·f(x)
plt.subplot(2, 1, 2)
plt.plot(x_norm, y_norm_g, 'r-', label='g(x) = x·f(x)')
# 只填充到x=6的区域
plt.fill_between(x_norm[mask], y_norm_g[mask], alpha=0.3, color='red')

# 计算第二个子图中到x=6的积分值
integral_g_up_to_6 = np.trapezoid(y_norm_g[mask], x_norm[mask])
# 标注积分值
plt.annotate(f'x=6时的积分值: {integral_g_up_to_6:.2f}',
             xy=(6, 0), 
             xytext=(6-1, 0.3),
             arrowprops=dict(facecolor='black', shrink=0.05),
             fontsize=10,
             bbox=dict(facecolor='white', alpha=0.8))

# 绘制x=6的竖线
plt.axvline(6, color='purple', linestyle='--', label=f'x=6')
plt.axvline(mu, color='green', linestyle='-', label=f'期望 μ = {mu}')
plt.title('正态分布的加权函数 g(x) 与到x=6的积分')
plt.legend()
plt.grid(alpha=0.3)

plt.tight_layout()
plt.show()

# 打印结果
print(f"第一个子图（PDF）到x=6的积分值（累积概率） = {integral_pdf_up_to_6:.4f}")
print(f"第二个子图（g(x)）到x=6的积分值 = {integral_g_up_to_6:.4f}")
print(f"g(x) 下的总面积（期望） = {np.trapz(y_norm_g, x_norm):.2f}（理论值为 {mu}）")

# 因为篇幅原因，仅保留关键语句。学员可得完整 notebook
mu, sigma = 5, 1

# 定义 X，pdf, x·f(x)
x_norm = np.linspace(mu-3*sigma, mu+3*sigma, 1000)
y_norm_pdf = norm.pdf(x_norm, mu, sigma)
y_norm_g = x_norm * y_norm_pdf

mask = x_norm <= 6

plt.plot(x_norm, y_norm_pdf, 'b-', label=f'正态分布PDF')

# 计算第一个子图中到x=6的积分值（累积概率）
integral_pdf_up_to_6 = np.trapezoid(y_norm_pdf[mask], x_norm[mask])

# 计算期望
E = np.trapezoid(y_norm_g, x_norm)
plt.axvline(E, color='green', linestyle='-', label=f'期望= {E:.2f}')

# 计算子图1中，到 X=6 时的重心
area = np.trapezoid(y_norm_g[mask], x_norm[mask])
centroid = area / integral_pdf_up_to_6

plt.plot(x_norm, y_norm_g, 'r-', label='g(x) = x·f(x)')
# 只填充到x=6的区域
plt.fill_between(x_norm[mask], y_norm_g[mask], alpha=0.3, color='red')

# 计算第二个子图中到x=6的积分值
integral_g_up_to_6 = np.trapezoid(y_norm_g[mask], x_norm[mask])

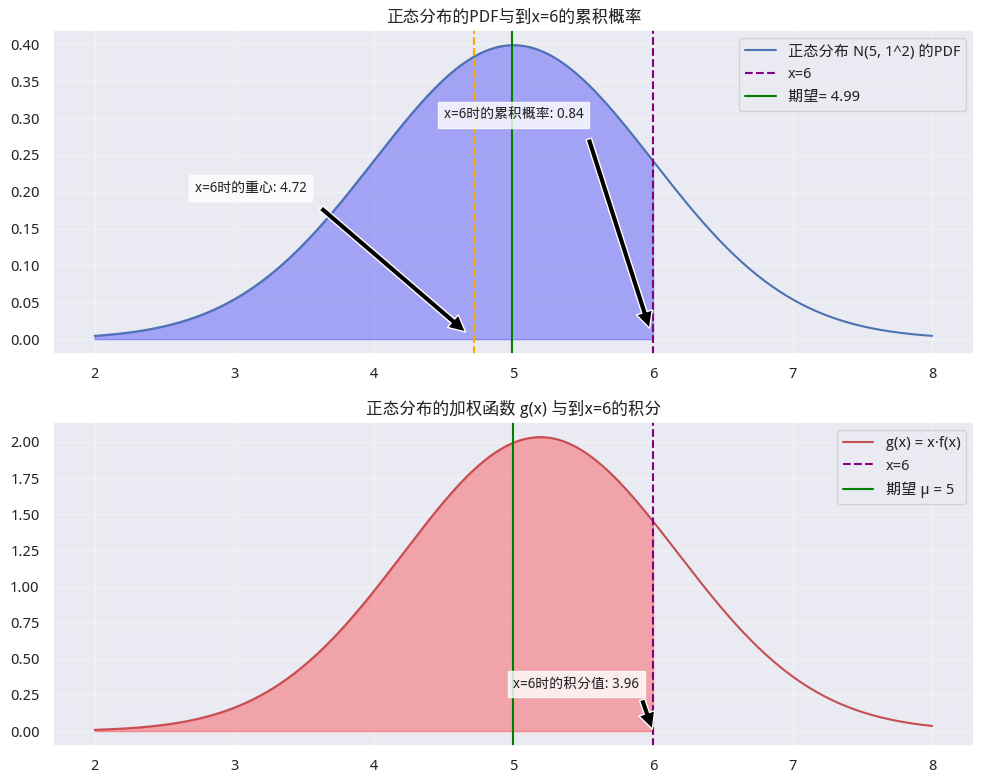图5 正态分布与期望

第一个子图是正态分布的密度函数图。它的积分是分布函数。当\(x=6\)时，\(P(X\leq x)=0.84\)。理论期望是5，实际计算出来的值（第14行代码）为4.99。

如果把正态分布密度函数图理解成为一座天秤，那么\(\mu\)的位置就正好在天秤的正中间，这就是期望是分布的重心说法的来由。

第二个子图是对\(g(x) = x.f(x)\)的积分。当 \(x = 6\)时，\(g(x)\)的积分为3.96。此时对应的分布的积分为0.84，因此，\(g(x)\)的重心为\(3.96/0.84 = 4.72\)。

Tip

随机变量 X 在 \(X \le t\) 时的期望公式（称为截断期望）是：

\[ E(X|X\leq t) = \frac{\int_{-\infty}^{t} x f(x) dx}{\int_{-\infty}^{t} f(x) dx} \]

我们把这个重心（线）也画在了图5中的第一个子图上。它是最左侧的橘色竖线。直觉上看，它确实是在 PDF 函数、随机变量 X 与竖线 X=6 围成的区域的几何中心上。

如果看了这么多，你还是感觉难以理解期望的积分算法，你可以尝试把 \(x\)或者\(f(x)\)看成一个常量，常量可以提取到积分式以外，这样就变成了一个简单积分--在物理意义上有更直观理解的东西。

『高阶』期望¶

在前面介绍的期望公式中，我们求得的是随机变量 \(X\) 的期望：

\[ E(X) = \int_{-\infty}^{\infty} x f(x) dx \tag {式1} \]

你可能要问，式子中的第一个 \(x\) 为何这样特殊？如果它本身也是一个函数，则式子：

\[ E(g(x)) = \int_{-\infty}^{\infty} g(x) f(x) dx \tag {式2} \]

有何含义？

首先，如果 \(g(x) = x\)，则式子（2）就退化为式子（1），即都是在求随机变量\(X\)的期望。如果\(g(x) = 1\)，则式子2还成为分布函数。

一般地，只要我们看到某个函数乘以概率密度再积分，那么它就是对该函数的期望。这就是式子2的含义。

这种推广有何意义？我们知道，离散随机变量是没有 PDF 的。但是，如果离散随机变量\(g(x)\)本身是一个分段函数，而在每一个分段区间，都存在着概率密度函数呢？

此时，式2本质上是对随机变量函数 \(g(X)\)进行加权平均，权重由 X 的概率密度 \(f(x)\) 决定，它就成为离散型期望在连续场景下的自然推广，是计算连续型随机变量函数平均值的基础工具。

Tip

如果\(g(x)\)是一个分段、常数型的函数（取值为\(X_1, X_2, ...X_i\)），且在每一段上\(f(x)\)的积分可记为\(P_i\)，则 \(\int_{1}^{i} g(x) f(x) dx = \sum_1^iX_i \cdot P_i\)。只要我们看到某个函数乘以概率密度再积分，那么它就是对该函数的期望。

n 个点共半圆问题¶

有了这些知识铺垫之后，让我们再回到本系列第一篇中提出的问题：

Question

一个圆里随机取 n 个点，它们在同一个半圆的概率是多少？

现在，我们可以用以下递归模型来求解此问题：

\[ P_n = P(X_n|P_{n-1}) \times P_{n-1} \tag{3} \]

\[ \begin{align} P(X_n|P_{n-1}) &= \int P(X_n|{\alpha_{n-1}}=x) f_{\alpha_{n-1}}(x)dx \\ &= \int_0^{2\pi} \frac{2\pi-x}{2\pi} f_{\alpha_{n-1}}(x) dx \end{align} \tag{4} \]

这里，\(P_n\)表示随机放置的 n 个点全部落在同一个半圆内的概率。同理，\(P_{n-1}\)是 \(n-1\) 个点全部落在同一个半圆内的概率。

\(X_n\)是事件，表明第\(n\)个点与前\(n-1\)个点同落在同一个半圆内。

\(P(X_n|P_{n-1})\)表示在前\(n-1\)个点已经落在同一个半圆内的条件下，第\(n\)个点也落在同一个半圆内的概率。

\(\alpha_{n-1}\) 表示在前\(n-1\)个点共半圆时，它们所能张出的最大夹角（即这\(n-1\)个点在半圆内分布时，最外侧两个点之间的圆心角，取值范围为\((0, 2\pi)\)。它也是一个随机变量。

\(f_{\alpha_{n-1}}(x)\)：随机变量\(\alpha_{n-1}\)的概率密度函数，表示\(\alpha_{n-1}\)取值为\(x\)时的概率密度。

\(P(X_n | \alpha_{n-1}=x)\)：在前\(n-1\)个点的最大夹角为\(x\)的条件下，第n个点能与它们共半圆的概率。

式3）很容易理解，它是用递推公式来表示第\(n\)个点共圆的概率。它的逻辑是，只有前\(n-1\)个点先共半圆，才有可能让第n个点加入并形成n个点共半圆的情况，因此是递归依赖关系。

式4）是全概率公式的连续形式。它的含义是，基于全概率公式，对连续随机变量\(\alpha_{n-1}\)的所有可能取值\(x\)进行加权积分。权重为\(\alpha_{n-1}=x\)的概率密度\(f_{\alpha_{n-1}}(x)\)，被加权项为该条件下第\(n\)个点能共半圆的概率\(P(X_n | \alpha_{n-1}=x)\)。

这里的表述尽管很复杂，但是，它的严谨性不言自明。在一下篇，我们将对它进行推导求解。这个过程，将把所有的知识（PDF 和期望），以及归纳法串起来。