algo »

蒙特卡洛：看似很高端的技术，其实很暴力很初级

#monte-carlo   #algo   #VaR  

---

Table of Content

我们常常想知道投资组合在未来的某一天，最大损失会是多少，估算方法之一就是蒙特卡洛。尽管它在计算性能上不占优势，却最让人心里踏实 -- 毕竟，它是一种把几乎所有的路径都走了一遍，再回来告诉你一路上的风险与风景的方法。

她看起来很高端，实际上只是很暴力。今天就带你认识她。

5 月 20 号那天，人工智能界出了个大事。Builder.AI 宣告破产。这是一家由印度裔创始人 Sachin Dev Duggal 于 2016 年在伦敦创立的公司，曾凭借“AI 驱动的无代码 App 开发平台”概念风光无限，估值一度高达 17 亿美元。

不过，2019 年起，《华尔街日报》的一篇报道撕开了 Builder.ai 的虚假面纱。多位前员工爆料，公司所谓的 AI 平台，大量功能实际上是靠印度工程师手动编码完成。随着时间推移，Builder.ai 的虚假商业模式逐渐难以为继，最终不得不于 5 月 20 日退出历史舞台。

Builder.AI 对他们的人工智能的能力进行了过度的宣传，本质上是欺骗和欺诈。不过，并不是所有的『过度宣传』都会被令人讨厌。我们今天要讲一个真实、广泛使用的技术，它其实很暴力很初级，但是被浪漫的科学家们冠称了一个高大上的名字：蒙特卡洛方法，从而变得『高端』起来。

蒙特卡洛方法（Monte Carlo），又称统计模拟方法，是一种通过随机抽样和概率统计来解决数学、物理、工程等领域问题的数值计算方法。其核心思想是利用大量随机样本模拟不确定性过程，通过统计规律近似求解复杂问题。

该方法起源于 20 世纪 40 年代，由数学家约翰・冯・诺依曼（John von Neumann）和斯塔尼斯拉夫・乌拉姆（Stanisław Ulam）在研究曼哈顿计划中的中子扩散问题时提出。由于此方法非常依赖于随机过程，与摩纳哥赌场里的赌博游戏有类似的随机性，因而得名。

它的最简单的一个版本是，用来计算圆周率。

1. 蒙特卡洛方法计算圆周率

假设我们有一个 2*2 的正方形，那么，它的内接圆的半径就是 1，面积就是\(\pi\)。根据几何概率，随机往这个正方形中投入一个点，它落入方形（包括内接圆）的概率当然是 1，落入内接圆的概率则是\(\pi/4\)。

因此，如果我们在区间【1，1】上生成若干个随机数对（\(X,Y\)），如果对其中的任意一个点\((X,Y)\)满足\(X^2+Y^2<1\)，那么这个点就落在内接圆内。只要我们加大随机对个数，那么，最终统计出来的落点数的占比，就代表了圆周率。

我们可以通过下面的代码来演示：

import numpy as np
import matplotlib.pyplot as plt

def estimate_pi(n_points=10000, visualization = False):
    # 生成均匀分布的随机点 (-1, 1)
    x = np.random.uniform(-1, 1, n_points)
    y = np.random.uniform(-1, 1, n_points)

    # 判断点是否在圆内 (x² + y² ≤ 1)
    inside = x**2 + y**2 <= 1

    # 计算圆周率估计值
    pi_est = 4 * np.mean(inside)

    # 可视化结果
    if visualization:
        plt.figure(figsize=(6, 6))
        plt.scatter(x[inside], y[inside], s=1, c='blue', label='Inside Circle')
        plt.scatter(x[~inside], y[~inside], s=1, c='red', label='Outside Circle')
        plt.title(f'Estimated π = {pi_est:.6f} (n={n_points})')
        plt.legend()
        plt.show()

    return pi_est

# 示例运行
for n in (100, 10000, 100_0000):
    pi_estimate = estimate_pi(n)
    print(f"Estimated Pi: {pi_estimate}")
    print(f"Error: {abs(pi_estimate - np.pi):.6f}")

n = 10_0000
estimate_pi(n, visualization = True)

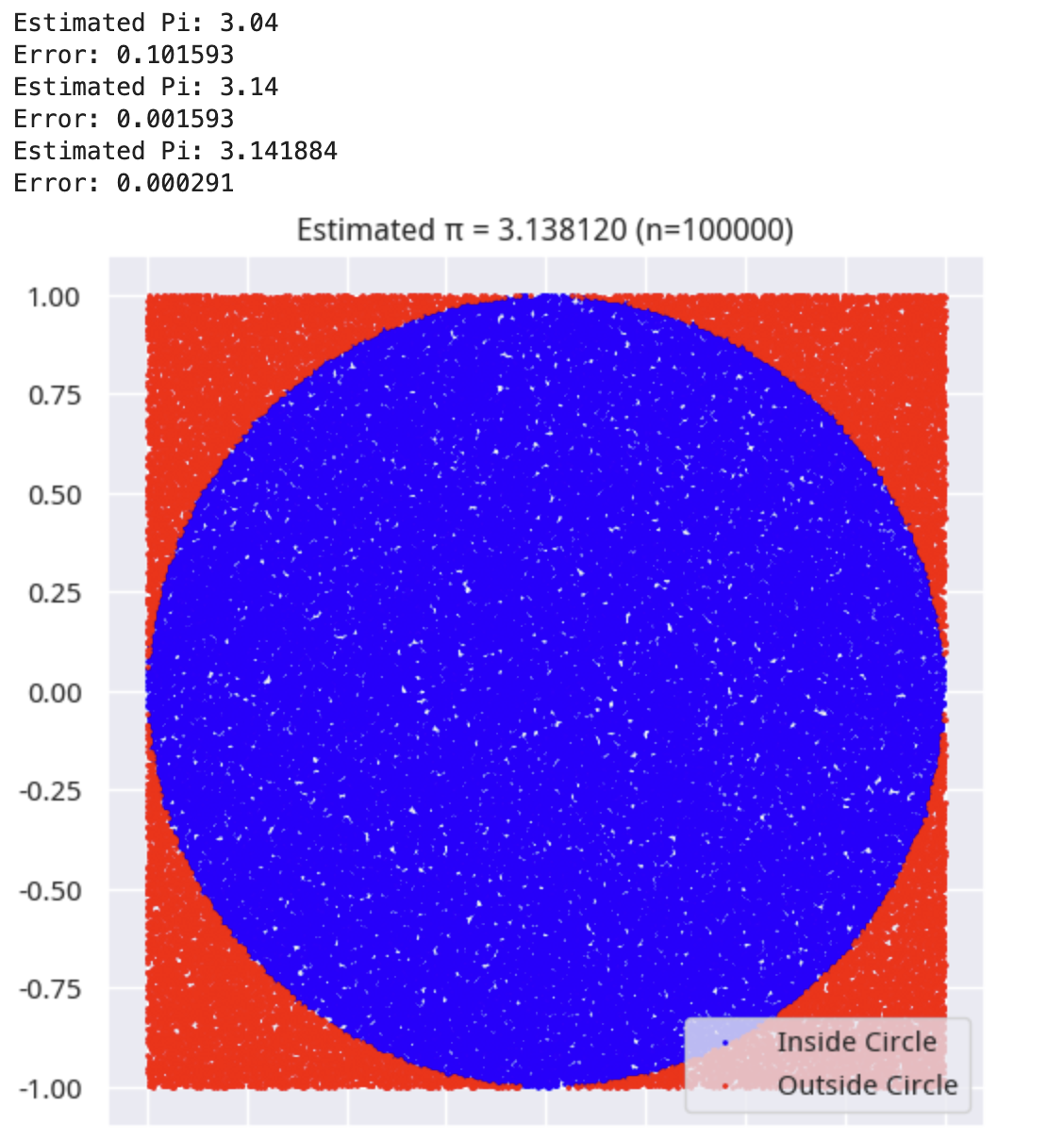
结果表明，当我们进行超过 100 万次随机试验之后，估计出来的\(pi\)值就已经很接近真实值了。这个计算简单粗暴，也只需要 10ms 就可以计算出来。虽然无论从精度还是性能上，都比不上莱布尼茨级数法，或者拉马努金公式和高斯 - 勒让德，但作为一个不烧脑子的算法，更让我这种学渣喜欢。

2. 蒙特卡洛方法计算 VaR

在量化领域，蒙特卡洛方法的优势则不止是简单，有时候甚至是不可替代的。这一切都是因为金融市场特有的随机性和难以预测性带来的。

VaR（在险价值） 是一种用于衡量金融风险的统计指标，表示在特定置信水平 和 持有期内，某一资产或投资组合可能遭受的最大潜在损失。

它可以用以下公式定义：

\[ P(L \geq VaR_\alpha) = 1 - \alpha \]

其中\(\alpha\)是置信水平。我们拿一个例子来解释这个公式，它表明，如果某投资组合在 95%置信水平下的日\(VaR\)为 100 万元，则意味着未来 20 个交易日中，可能会有一天的损失超过 100 万元。

作为一个风险指标，\(VaR\)得到了巴塞尔委员的背书。1996 年，巴塞尔委员发布《资本协议市场风险补充规定》，允许银行使用内部 VaR 模型计算市场风险资本要求，推动 VaR 成为全球金融行业标准。

在量化交易中，我们常常会想知道某个投资组合，在已知某些特征（比如波动率）的前提下，在未来的某一天，该组合的最大损失会是多少，以便做好风险管理（比如通过提前减仓来降低风险）。尽管有多种方法，但蒙特卡洛方法尽管计算性能不占优势，却往往最让人心里踏实 -- 毕竟，它是一种把几乎所有的路径都走了一遍，再回来告诉你一路上有哪些风险的方法。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 投资组合参数
initial_stock_price = 100    # 股票初始价格
stock_volatility = 0.2       # 股票年化波动率
risk_free_rate = 0.05        # 无风险利率
option_strike = 105          # 看涨期权行权价
option_maturity = 0.5        # 期权剩余期限（年）
num_options = -10            # 期权空头份数（负号表示卖出）
num_shares = 1000            # 股票多头数量
portfolio_value = num_shares * initial_stock_price  # 初始组合价值

# 模拟参数
num_simulations = 10000      # 模拟次数
time_horizon = 10/252        # 10 个交易日的时间跨度（年化）
dt = 1/252                   # 时间步长

# Black-Scholes 期权定价函数
def black_scholes_call(S, K, r, sigma, T):
    d1 = (np.log(S/K) + (r + 0.5*sigma**2)*T) / (sigma*np.sqrt(T))
    d2 = d1 - sigma*np.sqrt(T)
    return S * norm.cdf(d1) - K * np.exp(-r*T) * norm.cdf(d2)

# 计算当前期权价值
current_option_value = black_scholes_call(initial_stock_price, option_strike, 
                                          risk_free_rate, stock_volatility, option_maturity)

# 计算当前组合价值
current_portfolio_value = num_shares * initial_stock_price + num_options * current_option_value * 100  # 期权合约乘数 100
print(f"当前组合价值：${current_portfolio_value:.2f}")

这样我们就得到了一个随机组合，并且它的当前价值是$95418.32 元。

接下来，假设我们关心的是持有 10 天时，这个组合的收益和风险。我们不知道每个资产的涨跌将会如何演进，但是，我们可以这样『蒙』：

# 生成随机收益率路径
np.random.seed(42)  # 设置随机种子，确保结果可复现
daily_returns = np.random.normal((risk_free_rate * dt), 
                                (stock_volatility * np.sqrt(dt)), 
                                (num_simulations, int(time_horizon/dt)))

# 计算累积收益率和未来股票价格
cumulative_returns = np.cumprod(1 + daily_returns, axis=1)
future_stock_prices = initial_stock_price * cumulative_returns[:, -1]

# 计算未来期权到期时间
future_option_maturity = option_maturity - time_horizon

# 计算未来期权价值（考虑时间衰减和股价变动）
future_option_values = np.array([black_scholes_call(S, option_strike, risk_free_rate, 
                                                    stock_volatility, future_option_maturity)
                                for S in future_stock_prices])

# 计算未来组合价值
future_portfolio_values = num_shares * future_stock_prices + num_options * future_option_values * 100

# 计算组合价值变动（损失为负收益）
portfolio_changes = future_portfolio_values - current_portfolio_value
losses = -portfolio_changes  # 将负收益转换为正损失
losses

到现在为止，我们就得到了未来 10 天后，组合收益损失的一万种可能。

损益的一万种可能

接下来，我们就可以使用一个小小的统计技巧，来计算不同置信水平下的 VaR:

confidence_levels = [0.95, 0.99, 0.999]
var_values = {}

for cl in confidence_levels:
    var = np.percentile(losses, (1 - cl) * 100)
    var_values[cl] = var
    print(f"{cl*100:.1f}% VaR: ${var:.2f}")

# 计算 95%置信水平下的 ES（预期短缺）
var_95 = var_values[0.95]
es_95 = np.mean(losses[losses >= var_95])
print(f"95% ES （预期短缺）: ${es_95:.2f}")

95.0% VaR: $-3446.95 99.0% VaR: $-4387.73 99.9% VaR: $-5235.53 95% ES （预期短缺）: $14.24

这个组合真是个亏钱的利器啊。它有 95%的概率会亏$-3446.95 元。不过，95%ES 数据告诉我们，即使出现亏损的情况，那么超出亏损（-3446.95）的情况下，你也平均也只要再亏 14.24 元就 OK 啦。

3. 根据夏普来估计最大回撤

假设你有一个牛 x 的策略，在回撤中，得到的夏普是 2，一般来说这是个相当不错的策略。但是，你也知道，回测不可能完全等同于实盘，所以，你想知道：

Question

一旦我们把策略部署到实盘中，很不幸它开始回撤了。那么，当最大回撤达到多少时，我们就应该不再相信这个策略？

显然，我们不能拿当前的回撤与回测中的最大回撤简单比较。因为后者是一个标量，是没有统计意义的。但是，在实盘中，最大回撤是比夏普更灵敏、投资人更关注的指标，我们又必须回答这个问题：现在的最大回撤是否超出了夏普允许的范围，是否意味着策略已经失效？

我们在『匡醍。量化二十四课』中探讨过这个问题，用的正是蒙特卡洛方法。我们通过不同夏普指标下，5000 万次的模拟，得出了这样的答案，供大家在实盘中参考：

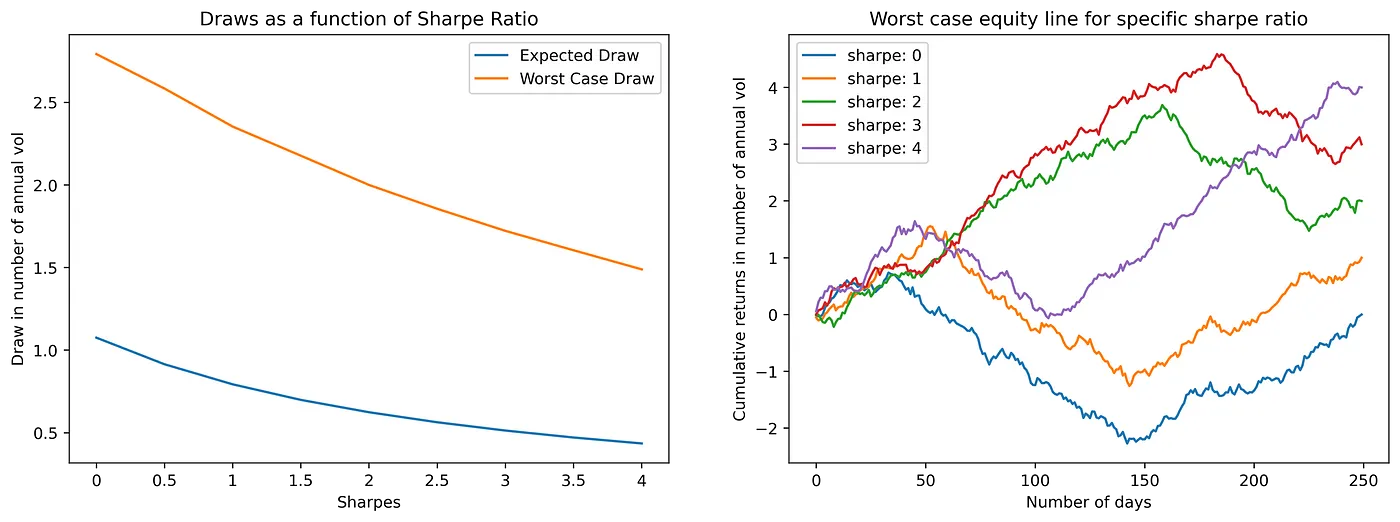
在这张图中，蓝色是正常情况，黄色是最坏的情况。X 轴是夏普率。这里的 Y 轴是什么呢？它并不是最大回撤本身，而是最大回撤相对于年化波动率的比值，这样会更科学一点。

以左图为例，在夏普率为 1.5 时，如果最大回撤是年化波动率的 0.7 倍，表明策略仍然处在正常状态；但你可能会在最大回撤超过年化波动率的 0.7 倍之后，考虑中止策略执行。如果最大回撤是年化波动率的 2.18 倍，则表明策略处于最糟糕的状态。如果已经处在这种状态，那么，也许可以期待一个小小的反弹，然后再退出策略。

Info

本文有可运行的 notebook 格式，可以匡醍好课平台免费获取。 我们也提供类似星球一样的服务，现在下单，每天不到 1 元钱，即可享有匡醍研究平台一年订阅权。您将获得： 1. 公众号付费文章的 notebook 版本。该版本自带数据和代码，全部可以运行。 2. Tushare 高级账号数据一年使用权，账号价值 500 元。