strategy »

KS Test, 广义双曲分布和抄底沪指

#statistics   #CDF   #KS-Test  

---

Table of Content

上一篇笔记我们抛出一个问题，沪指大跌 4%时，能不能抄底？今天的笔记，我们就通过 KS 检验，找出沪指的概率分布，进而回答这个问题。在后面的笔记中，我们还将换一个方法继续回答这个问题。

K-S 检验

第一个方法，是通过 K-S 检验，来碰碰运气，看看沪指涨跌是否刚好符合某个已知的分布。如果能找到，我们就可以轻松地由其连续密度分布函数 CDF，来计算出继续下跌的概率，即：

\[ P = cdf(-0.04) \]

---

K-S 是一种非参数检验，是统计检验中的一种。它可以用来检验一组样本是否来自某个概率分布 (one-sample K-S test)，或者比较两组样本的分布是否相同 (two-sample K-S test)。K-S 检验是以它的两个提出者，俄国统计学家 (Kolmogorov 和 Smirnov) 的名字来命名的。

我们可以通过 scipy.stats.kstest 来执行 k-S 检验。该方法的签名如下：

kstest(rvs, cdf, args=(), N=20, alternative='two-sided', method='auto')

这里 rvs 是随机变量状态，在我们接下来的示例中，我们将传入沪指 1000 个交易日的涨跌幅。在 cdf 参数中，我们传入要测试的随机分布名称。

返回结果为一个 KstestResult 类，它包括 statistic， pvalue 等重要属性。

现在，我们就通过 kstest，对 scipy.stats 中已实现的分布模型，逐一进行 One-Sample test，看看能否有通过检验的：

pct = close[:-1]/close[1:] - 1
dist_names = ['burr12', 'dgamma', 'dweibull', 'fisk', 'genhyperbolic', 
              'genlogistic', 'gennorm', 'hypsecant', 'johnsonsu', 
              'laplace', 'laplace_asymmetric', 'logistic', 'loglaplace',
              'nct', 'norminvgauss']

---

xmin, xmax = min(pct), max(pct)
dist_pvalue = []

for name in dist_names:
    dist = getattr(scipy.stats, name)
    if getattr(dist, 'fit'):
        params = dist.fit(pct)
        ks = scipy.stats.kstest(pct, name, args=params)
        dist_pvalue.append(round(ks.pvalue, 2))

df = pd.DataFrame({
    "name": dist_names,
    "pvalue": dist_pvalue
})

df.sort_values("pvalue", ascending=False).transpose()

我们将得到以下输出：

图可能有点宽，导致手机上没法看清楚。不过我们只要知道，这里的第一行，genhyperbolic，即广义双曲分布的 pvalue 最高，达到了 0.97。

注意 scipy.stats.kstest 中的 pvalue 可能跟我们在别处理解的 pvalue 不太一样，在它的说明和示例中，p 值大于 0.95，则可以认为在 95%的置信度下，认同原假设：即 rvs 来自于 CDF 所表明的那个分布。

---

因此，上述输出表明，genhyperbolic，即广义双曲分布，是所有假设中，沪指最接近的分布。

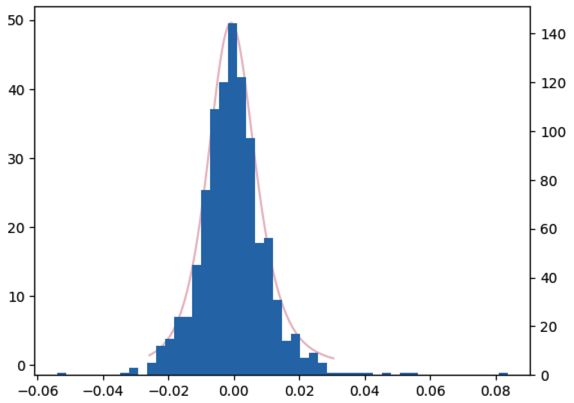
我们可以通过绘图来验证一下这个结论是否正确：

from scipy.stats import genhyperbolic

params = genhyperbolic.fit(pct)
rv = genhyperbolic(*params)

fig, ax = plt.subplots(1,1)
x = np.linspace(rv.ppf(0.01), rv.ppf(0.99), 100)
ax.plot(x, rv.pdf(x), label = 'genhyperbolic pdf', color="#EABFC7")

ax2 = ax.twinx()
_ = ax2.hist(pct, bins=50)

---

不能说十分相似，简直是一模一样。pdf 函数曲线刚好框住了实际分布直方图的外轮廓。

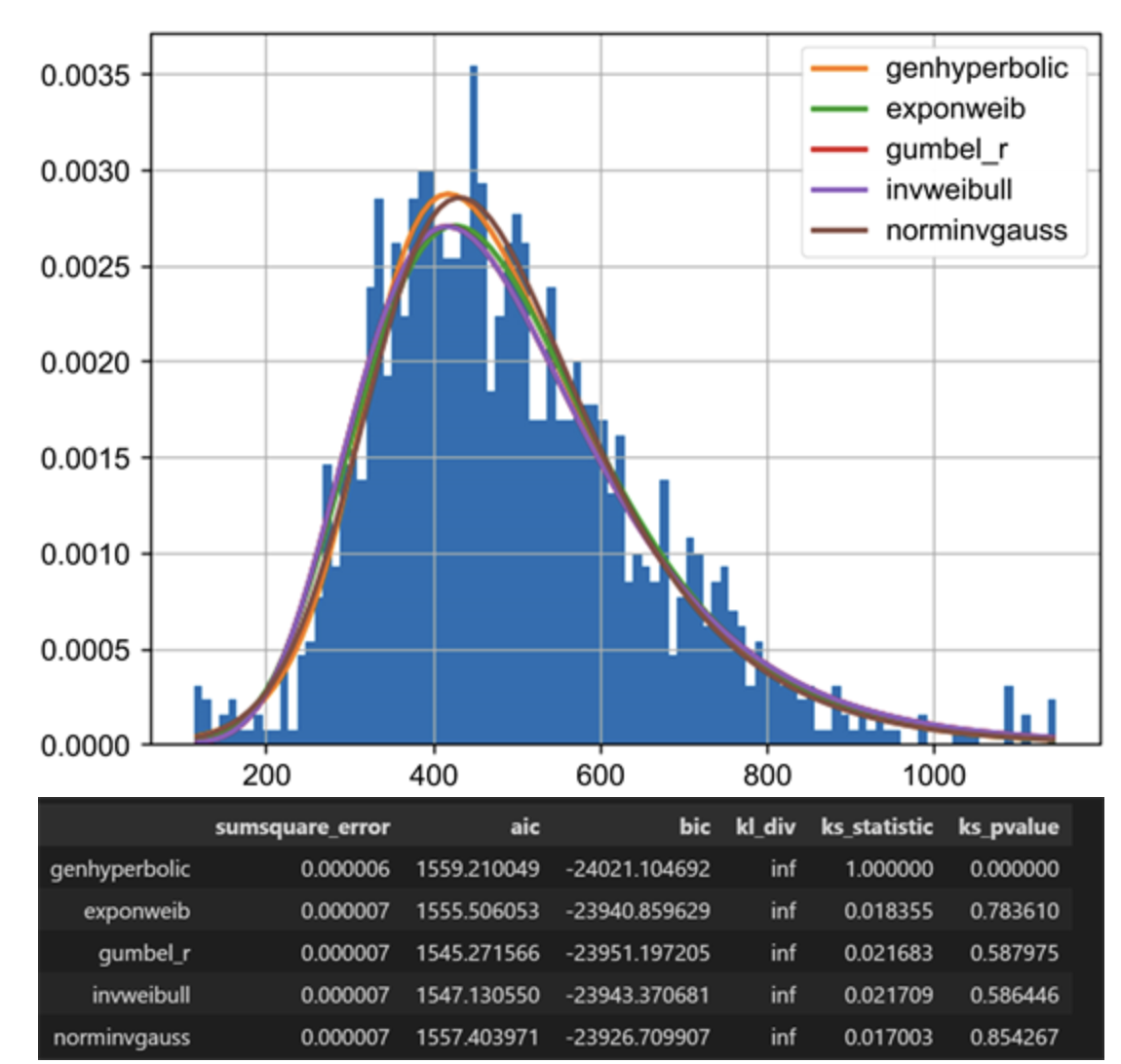
实际上，并非只有沪指符合广义双曲分布。根据 Souto 发表在《金融数学》（2023年2月）杂志上的文章，《Distribution Analysis of S&P 500 Financial Turbulence》, 标普 500 也是最接近这个分布。

Warning

Satou 没有使用 scipy.stats 中的 ks-test，而是自己实现了一个。证据之一就是，尽管他得出了标普接近于 GH 分布这一结论，但此时他计算出的 p-value 为零，而不是接近 1。细心的读者应该注意到，我们前面指出过，即 scipy 中的 ks-test 中的 pvalue，与其它地方看到的可能不一致。

类似的不一致还发生在对凸函数的定义上。一部分人（包括我）总是把图形看起来像凸字的函数叫成凸函数，但有些人认为它应该是凹函数，因为它的二阶导是负的。我曾经失去过一位既美丽又聪明的女同事，不知道是否就因为这个分歧。总之，既然你知道了，不妨今后也注意下，不要因小失大。

现在，我们就来求广义双曲分布下，跌幅小于-4%的累积概率，也就是继续下跌的概率：

---

from scipy.stats import genhyperbolic

params = genhyperbolic.fit(pct)
rv = genhyperbolic(*params)
print(f"继续下跌的概率为：{rv.cdf(-0.04):.2%}")

结果表明，继续下跌的概率仅为 0.16%。所以，结论是：本答案仅依据历史数据，仅为演示和说明量化算法，不构成任何投资建议！

Tip

看不太懂为什么 cdf(-0.04) 代表继续下跌的概率？我们的课程会从直方图讲起，直到你看懂为止。

Revisit Connor's RSI

如果你对我们的 Connor's RSI 的笔记还有印象，可能还记得，Connor's RSI 的三因子之一，是当天涨跌幅在近 20 天里的排名（prank）。这个排名，实际上就是经验 CDF 函数的一个线性映射。看来，发明一个伟大的指标，其实也只需要掌握简单的统计学原理即可。